Numerical Simulation of Cavity and Hydrodynamic Force of the Sphere Water Entry in Consideration of Surface Wettability

SUN Zhao, CAO Wei , WANG Cong , WANG Wei

(1. Shanghai Institue of Spaceflight Control Technology, Shanghai 201109, China; 2. School of Astronautics,Harbin Institute of Technology, Harbin 150001, China)

Abstract: Based on the numerical simulation method, this paper carried out the numerical research of vertical water entry of spheres, and focused on the influence of the surface wettability on the developing process of the water entry cavity. The results of cavity formation, trajectories, velocities, accelerations, and hydrodynamic force acting on the sphere are presented. The numerical method is based on Naiver-Stokes equations, by using the VOF model the interface is captured, and surface wettability was introduced through the CSF method. The numerical results are directly compared with the experimental results from the literature, which verifies the accuracy of the numerical method. Results show that surface wettability has a significant effect on the water entry cavity, especially in relatively low speed. The hydrophilic sphere falls faster and meets smaller drag while the hydrophobic sphere falls more slowly and brief mutation will happen in the motion when cavity is pinched off. In the early stage of water entry, the formation of fluid film movements on the surface of the sphere is the critical factor that leads to the formation of water entry cavity. For hydrophilic sphere, the fluid film moves upward along the sphere surface and forms up sputtering flow in the sphere vertex positions and does not produce the water cavity; for hydrophobic sphere, the fluid film detaches from sphere surface, which leads to air entrainment and the formation of water entry cavity.

Key words: multiphase flow; numerical simulation; water entry; cavity pinch-off;hydrodynamic force; surface wettability

0 Introduction

The water entry problem has been studied for centuries and remains of interest today[1-2].The water entry problem is a complicated interaction between solid and liquid. In recent years,with the development of modern scientific research, such as high-speed camera, high-speed particle imaging technology, researchers found that some of the physical mechanism in the process of water entry ignored by predecessors play an important role. Many engineering problems and natural phenomena are involved with the water entry problem, such as air to sea weapons[3],ship slamming[4], ricochet[5], torpedo[6], water walking creatures[7], etc.

Research about the water entry problem can be traced back to a century ago, Worthington & Cole[1-2]carried out a large amount of experimental observations to water entry phenomenon of spheres and other objects.

The role of high-speed imaging technology in capture the instant of water entry is crucial, and has been widely used in early water entry research. Aristoff et al[8-10]studied the water entry of decelerating spheres, the problem of water shock and the water entry of small size hydrophobic sphere in condition of low bond number.

Truscott and Techet[11-13]investigated the phenomenon of vertical water entry of spinning sphere, which has shown that rotating causes the different relative speed of the two sides of the sphere, resulting in a asymmetric water entry cavities, and eventually leads to trajectory deflect. At the same time, they also carried out the corresponding experimental research on the water entry of projectile and spinning spheres walking on water[14-15].

Dulax[16]studied the transient cavities created by the free fall of the sphere and cylinder impacting on the free surface, and presented an experience formula of the cavity profile, which is, to a certain extent, consistent with the experimental results.

Seiichi Sudo[17]covered the ferromagnetic sphere surface with a layer of magnetic liquid,and exerted alternating magnetic field in the water area, and the experimental results showed a complicated water entry cavity.

Bergmann[18]studied the water entry cavity and the drag coefficient of disk that vertically enters the water at a constant speed.

In recent years, the condition of sphere surface, especially the influence of surface wettability on the water entry problem catches attention, however, related research are still less.

May[20]found the water entry cavity is not easily formed when the sphere is already wetted,whereas the sphere surface covered with a layer of ash will produce larger water entry cavity.

Duez[21]studied the water entry phenomenon of hydrophilic and hydrophobic spheres, and found only the velocity above a critical value that the water entry cavity is produced and the surface contact angle has a great influence on the critical velocity.

In numerical simulation aspect, Doquang and Amberg[22]made use of the numerical calculation by coupling method of Navier-Stokes equation and Cahn-Hilliard equation, simulating the water entry of spheres with different wettability in different liquid mediums and the numerical results obtained a large amount vector field images of water entry cavity.

Mirzaii[23]adopted CSF model considering the surface tension and surface contact angle,the process of vertical water entry of sphere is simulated, the numerical results and experimental results are compared.

This paper studied the process of vertical water entry of the sphere through numerical method, emphasizing on the influencing of the surface wettability. Firstly, the numerical method is introduced, and the numerical results are compared with the experimental results from the literature to validating the accuracy of the numerical method. Then studies of the different surface contact angle of vertical water entry phenomenon, analysis about the displacement, velocity, acceleration in the process of water entry, and the hydrodynamic force acting on the sphere during the process of the water entry are shown. Through the observation of the development process of initial water entry cavity, the forming mechanism and development process of the water cavity and the subtle changes of flow characteristics of early water entry are analyzed.

1 Numerical method

1.1 Governing equations

The objective studied in this paper is the water entry of sphere at relatively low speed,where the system contains two kinds of fluid, the gas phase and liquid phase, respectively. The system can be treated as Newtonian fluid, incompressible and impenetrable. The transient,three-dimensional numerical simulations of the sphere motion in a water entry process are performed by using the Navier-Stokes equations. In this method, we solve momentum equation and continuity equation.

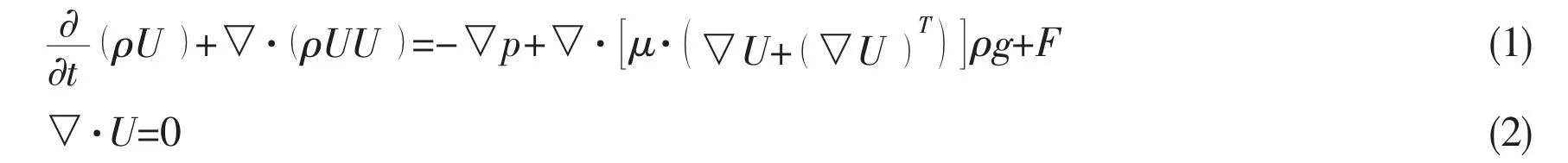
where ρ denotes the density, μ is the dynamic viscosity, U is the velocity, p is the pressure, g is the gravity acceleration, t is time, F represents the volume source term generated by the surface tension force.

According to the VOF (volume of fluid) method, the mixture’s physical properties are derived from the volume fraction of each phase. The average value of ρ and μ in a computational cell can be computed from the liquid phase volume value αlin accordance with:

where ρland ρgare densities of the liquid phase and gas phase, respectively, μland μgare the dynamic viscosities of liquid phase and gas phase, respectively. The detail material properties involved in numerical calculations are shown in Tab.1.

The liquid volume fraction distribution αlcan be determined by solving a separate passive transport equation, and given as:

Tab.1 The properties of liquid and gas phase in the numerical process

The continuum surface force method (CSF)[24]is used to describe the surface tension force.The surface tension F in Eq.(1) according to the CSF model is computed as:

For two-phase system, κi=-κj, ▽αi=-▽αj, then Eq.(6) is simplified as:

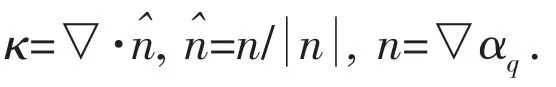
Wall adhesion is included in the model through the contact angle:

1.2 Computational domain and boundary conditions

Fig.1 illustrates the computational domain and boundary conditions, where Fig.1(a) is the three-dimensional computational domain in numerical calculation process, Fig.1(b) shows the two-dimensional diagram for understanding easily.

Computational domain axial length is 40D, the free surface is set at the center of the axial, namely the 20D. The position of the sphere is set just before the contact of free surface and its initial velocity U0is given. In order to save computational cost, considering the sphere for vertical movement only, without any horizontal movement, so a quarter model is modeled,as shown in Fig.1(a).

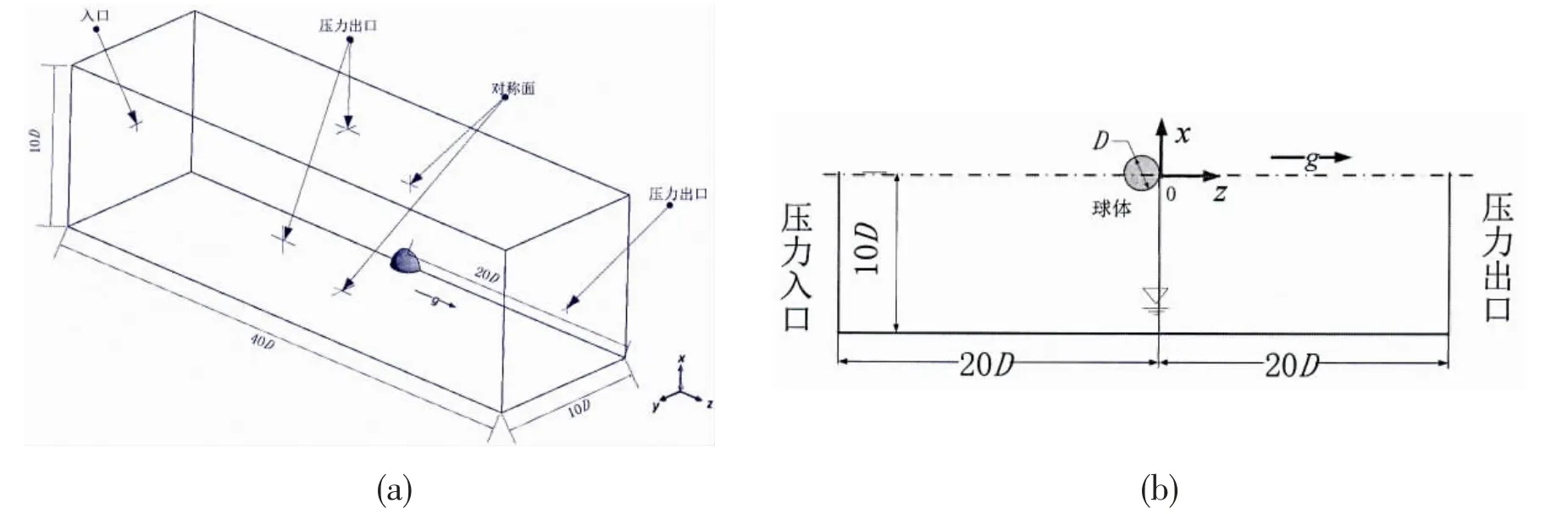
Fig.1 Computation domain and boundary condition

Finally, the overall dimension of the computational domain is 10D×10D×40D. Gravity g direction and the axis z direction are consistent, z axis through the sphere center, the coordinate zero point z=0 is defined at the free surface, time zero t=0 ms is defined as the instantaneous moment of the sphere contacting the free surface.

The grid was generated by using the commercial software ANSYS ICEM as a pre-processor for mesh generation, as shown in Fig.2. In the present research, the structured mesh is employed throughout the whole domain, and O-grid is built around the sphere to improve the whole grid quality. The mesh around the sphere is denser than the far-field.

Fig.2 Mesh generation around the sphere

The numerical simulations were carried out using ANSYS FLUENT software, a finite-volume code in dealing with multiphase flow problem. The boundary conditions, initial conditions,user defined functions, and the method of solving each equations are all specified in a user interface. The SIMPLE algorithm is used for coupling between pressure and velocity with a greengauss cell based gradient evaluation option to solve Reynolds-Averaged Navier-Stokes (RANS)equations. All the solution variables were solved via second order upwind discretization scheme for improving accuracy. The PRESTO (pressure staggering option) scheme is used for the pressure interpolation. Standard k-ε model[25]is carried out in the software ANSYS FLUENT.

The time step convergence was monitored and the simulation was considered to have converged when residuals of all conserved variables fell below 1e-5. The simulations were per formed on a Linux PC-cluster with 20 processors. In dealing with approximately 10 000 timesteps with a million cells and nodes, the computation took about two days for each case of simulation.

2 Results and discussion

2.1 Numerical verification

In this section, the numerical results of the water entry of sphere are presented, and the numerical results are directly compared with the experiments from the literature Aristoff[8]. In simulation process, the sphere diameter D, the solid-liquid density ratio ρ*= ρspere/ρliquid, surface contact angle θ, and kinematic parameters are consistent with the experiments from literature, see Tab.2.

Fig.3 shows the comparison between numerical and experimental results of the development process of the vertical water entry cavi-ty created by the sphere. Fig.3(a) is the numerical results, Fig.3(b) is the experimental results from the literature Aristoff[8]. As shown in Fig.3, the numerical results are in good agreement with the experimental results. The shape of the cavity and the recoil of water are well predicted by the present numerical model.

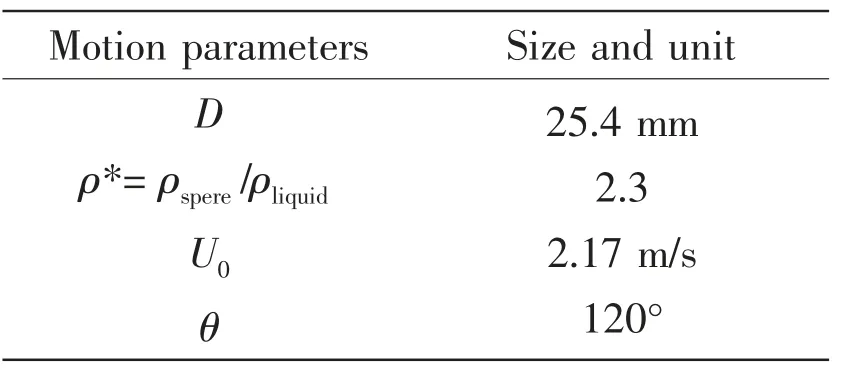
Tab.2 Sphere parameters in simulation

Fig.4 shows the comparison of the displacement of the sphere during water entry between the numerical results and experimental results from the literature[8]. The solid line indicates the numerical result, the dot line indicates the theoretical result, and the square symbol denotes the experimental result. As observed, the results of simulations agree well with those of the experimental and theory results.

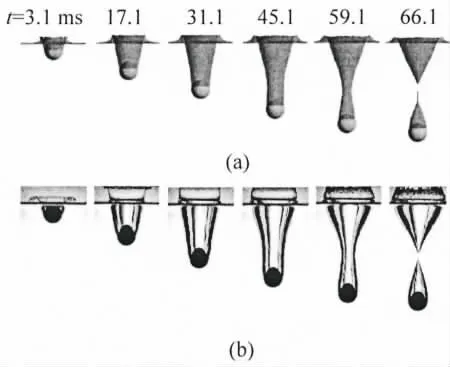
Fig.3 Comparison of numerical result and literature result

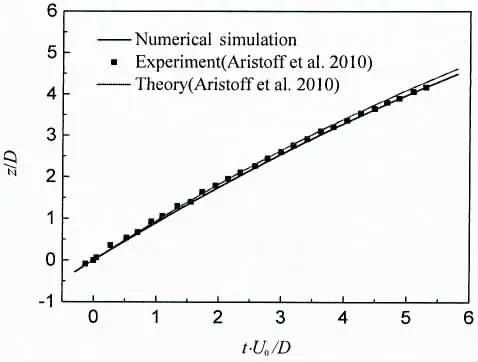
Fig.4 Sphere depth versus time for the impact sequences shown in Fig.3

2.2 Overall cavity shape

Fig.5 shows the typical process of sphere vertically entering the water. The impacting speed U0=2.7 m/s, the density of sphere ρ*= ρsphere/ρwater=2.7, the sphere diameter D=25.4 mm. The instantaneous of sphere contact with the free surface is defined as t=0 ms. The first picture in Fig.5 is taken at 1.2 ms after impact.

As illustrated in Fig.5, the water entry cavity surface expands quickly in the circumferential length scales and vertical direction. As the sphere descends, it gives each layer of water an outward horizontal velocity. Under the joint action of the fluid static pressure that depends on the depth and the internal pressure change of cavity, the outward expansion speed slows down and finally changes direction. In the end, the cavity pinch off at a certain depth below the free surface, and forms an ‘hourglass’ water cavity shape (Fig.5 t=61.2 ms).

After pinch off occurs, the cavity is divided into two parts, the upper cavity moves to the free surface and the volume becomes gradually smaller, and the lower cavity continues falling with sphere and finally collapses.

The water entry cavity shown in Fig.5 is a typical ‘hourglass’ cavity shape formation process. When the surface changed, the water entry cavity is not always the ‘hourglass’ shape.

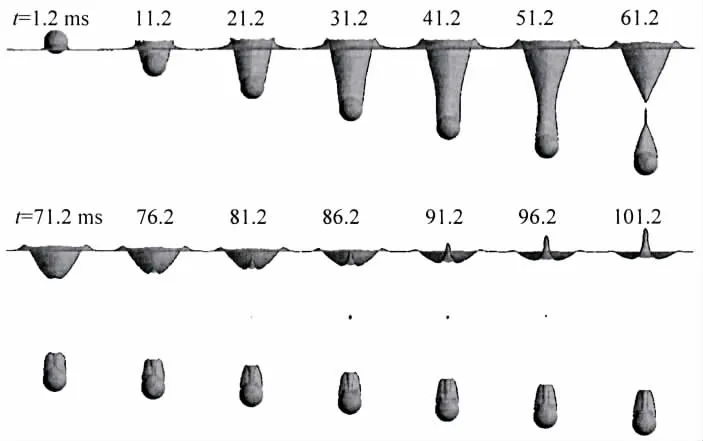
Fig.5 The developing process of water entry cavity created by sphere

Fig.6 illustrates the water entry cavity created by hydrophilic sphere and hydrophobic sphere. The water entry velocity is U0=2.37 m/s, time interval between pictures is Δt=8 ms, the contact angle is θ=30° for hydrophilic sphere, and θ=150° for hydrophobic sphere. As illustrated in Fig.6, for the hydrophilic sphere, only a simple vertical jet ejecting out from the free surface of the water, the sphere is completely wrapped in liquid during its descend, there is no water entry cavity generated; whereas for the hydrophobic sphere, liquid separation from the sphere causes air entrainment, forming an opening into the water bubbles, the cavity pinches off at a certain depth under the free surface,forming a typical hourglass shaped water entry cavity. We content that the transition from the non-cavity formation to the deep seal cavity formation is not sudden, there has a transition state between them.

Fig.6 Water entry cavities created by hydrophilic and hydrophobic spheres

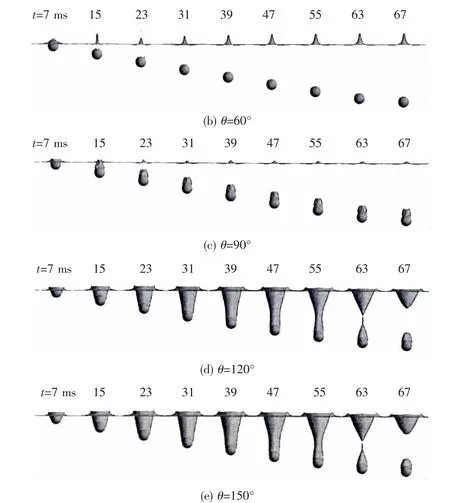
Fig.7 Water entry cavity created by sphere with different wetting properties

Fig.7 shows five development processes of water entry cavity created by sphere with different surface wettability, the surface contact angle are θ=30°, 60°, 90°, 120°, 150°, respectively. In addition to the different surface wettability, the other kinematic parameters are the same: the water velocity U0=2.5 m/s, density ρ*= ρsphere/ρwater=2.7, sphere diameter D=25.4 mm.The instant time of sphere impacting on the free surface is defined as time zero t=0 ms.

Fig.7 (a) and (b) show two kinds of sphere surface contact angle, θ=30°, 60°, respectively. The two water entry processes are very similar, neither of them causes cavity formation.

In Fig.7 (c), when θ=90°, the sphere tail follows cavity. However, this cavity does not have process of expansion, contraction, pull away, and pinch off, it quickly shrinks at the free surface and the cavity decreases in size as the sphere descends.

As shown in Fig.7 (d) and (e), when the sphere surface contact angle increases, the cavity shape is very similar to the typical entry cavity in Fig.5, after the cavity is through extension, drag, shrinkage and other processes and pinches off at a position below the free surface,eventually forming the typical ‘hourglass’ shaped water entry cavity.

2.3 Displacement, velocity and acceleration

In the process of water entry, in addition to the formation and the development of the water entry cavities which catch wide attention, the kinematic characteristics and the influence to hydrodynamic force acting on the sphere are also the research focus.

Fig.8 illustrates the displacement of the sphere during water entry with different surface wettability. The surface contact angles are θ=30°, 60°, 90°, 120°, 150°, respectively. In addition to the different surface contact angles, other movement parameters are the same as Fig.7.The instant time of sphere impacting on the free surface is defined as time zero t=0 ms. The vertical downward direction is defined as positive direction. As shown in Fig.8, different sphere has experienced different decelerating displacement, and the hydrophobic sphere such as θ=150° falls more slowly.

Fig.7 and its corresponding description show that when the sphere descends during vertical water entry, it gives each layer of surrounding water about a horizontal expansion speed, which is a process of transferring the kinetic energy from the sphere to the surrounding fluid.

For the case that the water entry process does not produce cavity, the sphere movement has no significant damage on the original static fluid, the kinetic energy transfer is very small.The process to produce the water entry cavity will have most of the kinetic energy transferred to the surrounding fluid, makes the cavity wall extend around, therefore the hydrophobic sphere falls more slowly. The sphere becomes more hydrophobic, the more likely it is to generate large cavity, which indicates that the kinetic energy of the spheres will lose more and the falling speed will be slower.

Fig.8 The displacement versus time during water entry

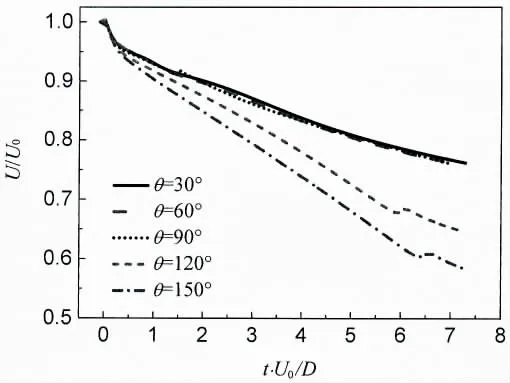
Fig.9 Velocity versus time during water entry

Fig.9 shows the velocity of the sphere during water entry with different surface wettability. Initial water movement parameters and the surface wettability are the same with those in Fig.7. It can be seen from the diagram, the speed of hydrophobic sphere is obvious attenuation falling faster than hydrophilic sphere. At the moment of t·U0/D=6-7, the fluctuation of two hydrophobic sphere movement speed happened. The stage of the volatility is mainly due to the pinch off occurrence, cavity wall is moving inward, at the same time due to downward flow of sputtering, which leads to connected sphere cavity volume sharply decreasing and the pressure increasing, so that the speed of sphere suddenly increases. This sudden acceleration process can be seen in Figs.3-8 where acceleration can be further observed to change over time. For hydrophilic sphere, it does not create cavity and sphere in the falling process and is completely surrounded by the fluid around, so there is no this kind of mutation.

Fig.10 shows the acceleration of the sphere during water entry with different surface wettability. Vertical downward is the positive direction, negative acceleration is slow motion,positive acceleration is accelerated motion, and the amount of acceleration is dimensionless by the gravity acceleration g. Corresponding to the velocity versus time in Fig.9, when the phase of sphere collides with free surface, due to the impact of larger mutation of the media, the sphere produces large reverse acceleration. Reverse accelerations of several different spheres are almost the same, which shows wettability on the surface of the sphere has almost no significant impact on impulsive load resulted from the initial water entry of spheres.

As the sphere descends, the two spheres θ=120° and θ=150° both create cavities, at the moment of t·U0/D=6-7, the cavity pinches off, the positive peak value of acceleration appears when the accelerated motion of sphere happens in a very short time.

What is worth the notice is that, after the impact stage, the acceleration of the hydrophobic sphere that produces water entry cavity quickly leveled off after a certain value while the acceleration of hydrophilic sphere leveled off after a short fluctuation process, which is due to the movement of the thin liquid layer on the surface of hydrophilic sphere and this will have more specific analysis in the subsequent chapters.

Fig.10 Acceleration versus time during water entry

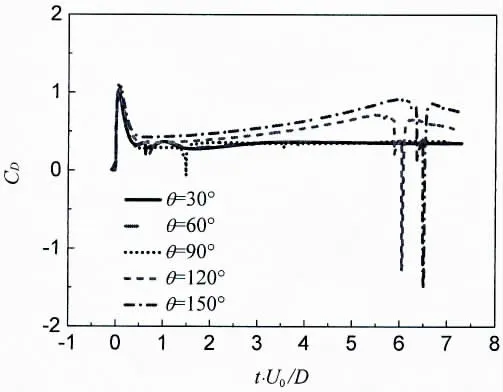
Fig.11 The drag coefficient versus time during water entry

Fig.11 shows the drag coefficient of the sphere during water entry with different surface wettability. Due to the direction of drag and velocity is opposite, therefore if the drag coefficient is positive, the motion is slow down; if the drag coefficient is negative, the motion is accelerated. As illustrated in Fig.11, the drag coefficient comes to a peak in the initial stage of water entry due to the impact, and when the cavity pinch-off occurs, a negative peak appears due to the pressure pulsation in the cavity.

2.4 Pinch-off time

Fig.12 illustrates the influence of surface contact angle on the pinch-off time. For hydrophilic sphere (θ＜90°) that there is no water entry cavity formation, with the increase of the surface contact angle, the liquid gathering on the top of the sphere. When the sphere surface is hydrophobic surface, pinchoff time has significant difference with hydrophilic sphere, transition from -1 soon arrived at 6-7.

Korobkin and Pukhnachov[1,26]explored the initial stage of the movement of object impact on free liquid surface, which shows that a thin liquid layer will form and climb up along the surface of moving object in the early stage of water entry.

Fig.12 Pinch-off time versus contact angle

Fig.13 Liquid film developing in the early stage of water entry

Fig.13 illustrates the formation of the thin liquid layer on the surface of the sphere in the early stage of water entry. For the hydrophilic sphere, as shown in Fig.13 (a), thin layer of liquid moves upward along the sphere surface, and finally gathers at the sphere pole, this item does not produce the water entry cavity; for the hydrophobic sphere, as shown in Fig.13 (b),thin layer liquid separates from the sphere at about the equator, which leads to the air entrainment and forms the water entry cavity.

3 Conclusions

In a word, researches on the water entry problem in consideration of surface wettability present unique opportunities for controlling water impact and the object trajectory at moderate impact speeds. The clear delineation between cavity formation and no cavity formation is intriguing, though not wholly unexpected, and can be combined to affect the object trajectory,velocity, acceleration, and drag coefficient in a controlled fashion. At relatively low speed,changing surface wettability can make a sphere or other objects generate a small amount of spillage or form a larger cavity when passing the gas-liquid interface.

In this paper, the numerical method is based on Navier - Stokes equations, the VOF model and CSF method are coupled to introduce the surface wettability in the process of numerical calculation. This method was successfully used in the water entry problem, the cavity morphology and the water entry displacement. Numerical results were compared to those of the experiments available in the literature and present a very good agreement.

By comparison of the cavity shapes and the analysis of the displacement, velocity, acceleration, and the drag coefficient, this paper illustrates the role of surface wettability on the process of sphere water entry. By numerical method, this paper presents the mechanism of water entry cavity formation. The thin liquid layer produced in the early stage of water entry is the key factor for the water entry formation.

In addition, we note that the numerical simulations of wetting phenomena in water entry problem are scarce in literature, and that the present study provides a nice challenge for the development of numerical methods.