一类图的谱

曾建宇，何常香

（上海理工大学 理学院，上海 200093）

1 基本概念及背景介绍

图的谱可以反映出图的许多性质，图以上3 种特征值都是图的同构不变量。完全图又是图论中一类基础而重要的图，其结构的特殊性导致了它的研究方法的差异性及其结果的简洁性。Bergstrand 等[1]和Hartsfield 等[2]分 别 在1986 年 和1992 年对完全图和完全二部图进行研究并得到一些结论[1-2]。同时文献[3]也得到一些关于连通图谱半径的结论。本文主要研究特殊图类Hn,Km的各种谱，Hn,Km是对书图的一个推广。对于一个给定的图类，确定该图类中图的邻接谱半径的上界并刻画达到该上界的图，这是Brualdi 和Solheid 在1986 年提出的关于图的谱半径的一个问题[4]。此后，这些问题得到广泛研究，被称为Brualdi-Solheid问题。关于图的Brualdi-Solheid 问题的研究对于研究图的特性有着重要意义，文献[5-7]按照邻接谱半径对某些图类进行了排序，其中文献[7]首先找到了具有给定匹配数的双圈图的最大邻接谱半径。

同时，Brualdi-Solheid 问题也被移植到图的拉普拉斯谱半径和无符号拉普拉斯谱半径研究中。文献[8]利用树的阶数给出了树的Laplacian 矩阵的最大特征值的分布；文献[9]利用阶数给出了 n阶单圈图的Laplacian 矩阵的最大特征值的第一、第二、第三、第四大值及最小值。此外，对具有固定不变量的图的谱半径也有一些研究结果。特别是在文献[10-11]中，分别讨论了具有固定最大度的 n个顶点上的树和单圈图的谱半径。

本文计算邻接矩阵、拉普拉斯矩阵和无符号拉普拉斯矩阵的特征值，考虑在顶点数N=m(n+1)固定的情况下，给出了邻接谱半径的上界和拉普拉斯、无符号拉普拉斯谱半径的上下界，并刻画了达到上下界的极图。

定义1 设 Km是m阶完全图，取n+1个Km，将其中一个Km（主图）的第i个顶点分别和其余的n个Km（辅图）的第i个顶点相连（i =1,2,···,n），所得到的(mn+m)阶完全关联图记为Hn,Km，其中n ≥2，m ≥2。

例如，书图H4,K2和12 阶完全关联图H3,K3分别如图1 和图2 所示。

图 1 书图 H4,K2Fig. 1 Book graph H4,K2

图 2 完全关联图H3,K3Fig. 2 Complete associated graph H3,K3

从定义不难看出Hn,Km邻接矩阵和度对角矩阵分别为

式中， Em表 示 m阶 单位矩阵。

故 Hn,Km的拉普拉斯和无符号拉普拉斯矩阵分别为

定义2[12]设 M为实对称矩阵，将其行列作相同的划分，其每一子块的平均行和作为元素按其子块的位置顺序构成的矩阵称为 M的商矩阵。

定义3[12]给定图 G，设V1,V2,···,Vk是V(G)的一个划分，若对任意i,j ∈{1,2,···,k}，Vi中的每一个点在 Vj中都有相同个数的邻点，则称V1,V2,···,Vk为均匀划分。

引理1[12]对于一个均匀划分，若 v是商矩阵B 对应特征值 λ的一个特征向量，则 Sv是实对称矩阵 M的对应特征值 λ的一个特征向量，其中 S为M的特征矩阵。

由引理1 显然可知，对于实对称矩阵 M，其商矩阵B 的特征值都是 M的特征值。

推论1 对于图 G的邻接矩阵A(G)，其任何商矩阵的特征值都是A(G)的特征值。

证明 设A(G)是图 G的邻接矩阵，SA是图G的一个商矩阵，S′A是SA的一个商矩阵。由引理1可知，SA的特征值一定是A(G)的特征值，同理 S′A的特征值一定是 SA的特征值。所以，S′A的特征值都是A(G)的特征值。

与推论1 同理，可得到推论2。

推论2 对于图 G的拉普拉斯矩阵L(G)和无符号拉普拉斯矩阵Q(G)，它们任何商矩阵的特征值都是L(G) 和 Q (G)的特征值。

商矩阵和均匀划分都是计算证明谱的关键工具。在推论3 中，定义均匀划分并进行证明。

推论3 设Hn,Km的顶点集合为，其中v1,···,vm是主图的顶点，是第 k 个 辅图顶点n)。则是Hn,Km的一个均匀划分。

从图Hn,Km的结构可知：当vi∈Vi，其中i∈{1,2,···,m}时，vi在 其所在的顶点集 Vi中没有邻点；在顶点集 Vk中 有且仅有1 个邻点，其中k ∈{1,2,···,m}且k ≠i；在顶点集Vm+l中没有邻点，其中l ∈{1,2,···,m} 且l ≠i；在顶点集Vm+l中有 n个邻点，其中l ∈{1,2,···,m}且l =i。

当vik∈Vm+k， 其中 i∈{1,2,···,n}，k ∈{1,2,···,m}时， vik在顶点集 Vl中有且仅有1 个邻点，其中l=k； vik在其他剩余的所有顶点集中都没有邻点。

综上，均匀划分得证。

2H n,Km的各种谱

定理1 主要计算Hn,Km的邻接谱。在证明过程中，主要利用了商矩阵和矩阵秩的相关结论。

定理1 图Hn,Km的邻接谱为，其中n≥2,m≥2。

1(m-1)×mO(m-1)×m(m-1)×m

λ=-1 A(Hn,Km)(m-1)(n-1)

式中： 为元素全为1 的 阶矩阵； 为全1 的重向量；和分别为阶全1 和全0 矩阵。综上可知是的重特征值。

设B2=(m-1)E-A(Hn,Km)，则

令C=(1-m)Em+A(Km)，因为

所以R(B2)=(n+1)m-(n-1) 。综上可知λ=m-1是A(Hn,Km) 的n -1重特征值。

由引理1 可知，商矩阵SAm的特征值即为A(Hn,Km)的特征值。

利用定理1 同样的计算证明方法，可得到Hn,Km的拉普拉斯和无符号拉普拉斯谱。

定理2Hn,Km的拉普拉斯和无符号拉普拉斯谱分别为

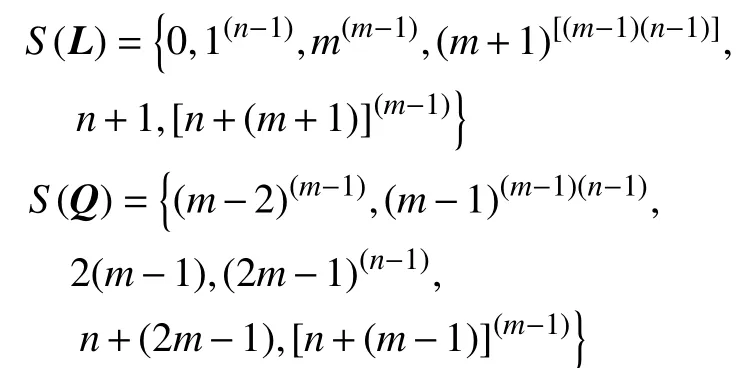
其中， n≥2,m ≥2。

3H n,Km 的谱半径

对于图Hn,Km可知其顶点数为N=m(n+1)，定义Hn,Km表 示所有点数为 N的图构成的集合。本文考虑当 N固定时，对图邻接谱半径的最大值和拉普拉斯和无符号拉普拉斯谱半径的最大和最小值分别进行计算证明。

定理3 设N=m(n+1)为固定值，且n≥2, m≥2。则对于任意 G∈Hn,Km，，等号成立当且仅当G=H2,K[N/3]。

证明 令f1=λ(G)，由定理1 中任一图的邻接谱可知， 其中n ≥2,m ≥2。因为N=m(n+1)，所以可知n与m成反比。假设m=n，则，所以可知当n=2时，λ(G)达到上界，此时极图为G=H2,K[N/3]。

定理4 设N=m(n+1)为固定值，且n≥2, m≥2，则对于任意G∈Hn,Km，，右边等号成立当且仅当G=Hm,Km，左边等号成立当且仅当G=H2,K[N/3]或G=H[N/3],K2。

与前两定理证明类似，下面研究对于任意G ∈Hn,Km，当其无符号拉普拉斯谱半径达到上界时的极图。

定理5 设N=m(n+1)为固定值，且n≥2,m ≥2。则对于任意，右边等号成立当且仅当 G =H2,K[N/3]，左边等号成立当且仅当G=Hm,K2m-1。