基于机载LiDAR的伪大光斑波形数据反演林分平均高
闫 灿,邢艳秋,高金萍,辛 颖,田 昕
(1.东北林业大学 森林作业与环境研究中心,黑龙江 哈尔滨 150040;2.国家林业与草原局调查规划设计院, 北京 100714;3.黑龙江省测绘科学研究所,黑龙江 哈尔滨 150040)
准确及时地估算森林结构参数对于森林资源管理以及碳循环和生物多样性研究具有重要意义[1-2]。其中,林分平均高指样方内所有林木的加权平均树高,作为估计其他参数的基础,对森林生物量/储蓄量估算及动态变化的研究至关重要[3]。利用多种遥感技术手段获取林分平均高可以有效进行森林资源估测[4-7],而激光雷达技术(Light detection and ranging,LiDAR)在林业研究中得到了广泛应用。
激光雷达系统可以获取相互独立的点云数据和波形数据,波形数据是未经处理的原始回波序列,点云数据由硬件系统直接产生[8]。当前,已有很多研究基于小光斑激光雷达(直径0.2~0.3 m)实现了林分平均高的提取,Qin 等[9]利用小光斑激光雷达获取的多次回波点云数据估算冠层高度;穆喜云等[10]基于冠层高度模型(Canopy height model,CHM)使用四分位数法估计林分平均高;焦义涛[11]通过设定植被高度平均值阈值的方式估测林分平均高。分析发现,基于小光斑离散点云数据可以有效估测森林林分平均高,但点云数据在估测树高方面存在着一些问题,如:点云分类算法、点云密度等,都会限制估测精度的提高。而波形数据相较于点云可以提高垂直结构信息含量,但小光斑由于光斑直径小的原因,造成了树顶无法被准确识别的问题,进而会影响树高的估计[12]。
针对上述问题,本研究提出以小光斑机载LiDAR 波形数据为基础,在波形数据高斯分解预处理的基础上,将高斯分量在时间轴上按脉冲能量比例以加权平均的方法进行叠加,最终形成一条类似大光斑LiDAR 波形的数据,即伪大光斑波形数据,旨在降低小光斑LiDAR 因光斑直径过小带来的影响,增加冠顶有效信息的获取,更加客观地反映样地内整体情况。在此基础上,分别基于小光斑LiDAR 波形数据和伪大光斑LiDAR 波形数据提取特征参数,并结合野外样方实测平均树高建立LiDAR 林分平均树高反演模型,进而进行比较分析。
1 研究区概况与数据来源
1.1 研究区概况
研究区为位于内蒙古自治区呼伦贝尔市额尔古纳上库力农场的依根农林交错区,地理坐标 位 置 为120°36′50.48″~120°52′56.53″ E,50°21′11.08″~50°24′32.00″ N(图1)。研究区地貌主要以山丘地形为主,气候为寒温带大陆性季风气候,境内主要河流为根河,主要生长着天然次生白桦林。

图1 研究区样地布设方案Fig.1 Sample layout scheme of study area
1.2 激光雷达数据
所用研究区数据采集于2012年8月26日,由运5 飞机搭载Leica ALS60 激光雷达扫描系统,坐标系采用UTM 投影坐标系和WGS84 大地坐标系,飞机飞行高度约为1 300 m。此次飞行获取的东西方向23 个条带数据覆盖整个研究区,激光雷达数据采集过程中飞行轨迹如图2所示。

图2 研究区飞行轨迹示意Fig.2 Diagram of flight trajectories
1.3 野外数据采集
为了使地面实测数据与激光雷达数据保持一致性,对研究区林分于2012年8―9月进行了野外调查。此次实地调查共设置了10 m×10 m 的方形样地80 个,借助Trimble GeoXT6000 GPS 对样地的中心点进行定位,定位精度达50 cm,结合Vertex IV 超声波测高测距仪、胸径尺和皮尺分别测量每木树高、枝下高、胸径及冠幅。野外数据测量结果如表1所示。

表1 野外数据基本统计量Table1 Basic statistics of measured data
基于Lorey's 平均树高方法计算林分平均树高,公式如式(1)所示。

式(1)中,hi为第i棵树的树高(m),hL为林分的平均树高(m),n为样地树木的株数,gi为第i棵树木的胸高断面积(m2)。
2 研究方法
2.1 激光雷达数据预处理
原始波形数据读取后采用高斯分解方法进行预处理,主要包括原始波形平滑去噪、高斯分量拐点计算及左右拐点确定、初始特征参量估计和高斯分量的波形拟合过程。本研究通过四分位数方法进行波形去噪,即设定原始波形振幅的某一四分位数为阈值以剔除噪声。拐点是依据高斯函数二阶导数的情况来判断。在确定左右拐点后,根据公式计算高斯分量的初始特征参数,包括位置、半波宽和振幅。波形拟合则采用非线性最小二乘法。
2.2 伪大光斑波形拟合
2.2.1 权数获得
利用DIGSILENT依次搭建了代表①、②、③、④四类负荷分布状况的典型单电源辐射状配网拓扑模型如图1至图4所示。
预处理得到每条原始波形数据对应的高斯分量波形与高斯函数十分接近,其中,每一高斯分量波形与对应采样时间的积分即为脉冲强度值(图3),图中I2为返回信号的积分,物理意义为脉冲能量。
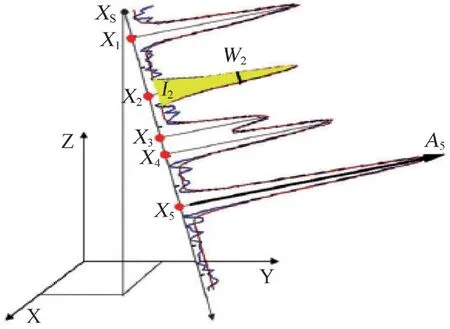
图3 全波形中的三维点与属性Fig.3 3D points and attributes derived from a waveform
以高斯函数为模型进行模拟,高斯函数的积分值对应曲线横轴上一定区间的面积,即脉冲能量值,其计算公式如式(2)所示。

式(2)中,A、t、σ分别为高斯分量中对应特征参数振幅、位置和半波宽,由波形预处理得到。
由高斯函数积分公式可知,高斯分量的面积与振幅和半波宽之积成正比,由此计算样地内各高斯分量脉冲能量占总脉冲能量的比例,并将其视为各高斯分量特征参数对应权数,计算公式如式(3)所示。

式(3)中,θi为样地内第i条高斯分量波形脉冲能量在总脉冲能量中的权数,Ai为样地内第i条高斯分量的振幅值,σi为样地内第i条高斯分量的半波宽,n为样地内回波波形分量的个数。
2.2.2 伪大光斑高斯函数模型的建立
在得到样方内各高斯分量波形脉冲能量占总脉冲能量权数的基础上,分别计算叠合后高斯函数的位置、振幅及半波宽,形成伪大光斑波形对应高斯函数模型。计算公式如式(4)所示。

式(4)中,n为样地内回波波形分量的个数,f(x)表示伪大光斑波形对应高斯函数模型。
2.3 参数提取

表2 回波波形参数说明Table2 Description of echo waveform parameters
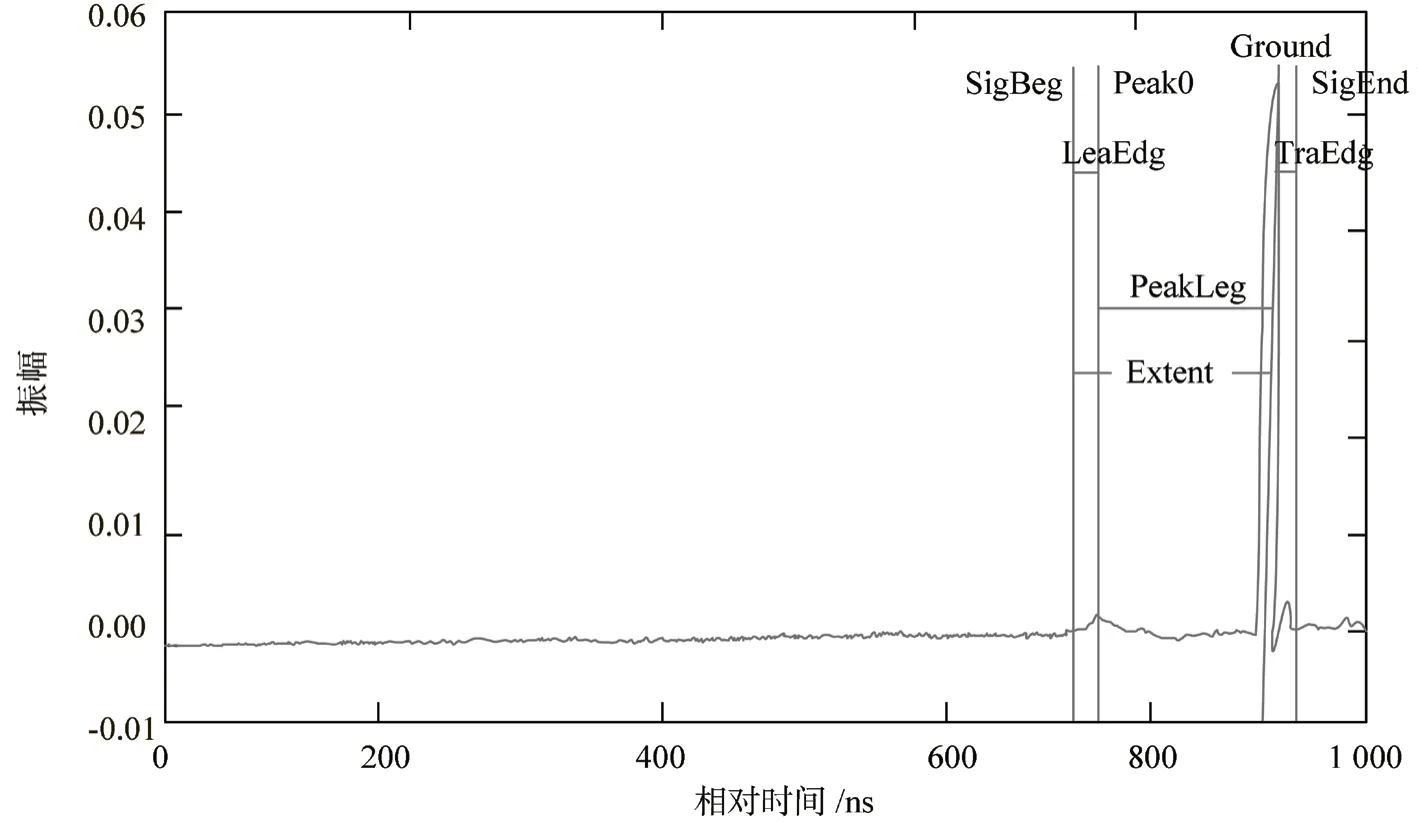
图4 大光斑波形参数示意Fig.4 Large footprint waveform parameter diagram
2.4 LiDAR 林分平均树高反演模型建立
森林垂直结构参数与波形数据关系密切,本研究提取波形长度(Extent)、波形后缘长度(TraEdg)和波形前缘长度(LeaEdg)等与平均树高相关的回波波形参数作为自变量,以野外实测平均树高H作为因变量拟建立平均树高反演模型。综合考虑研究区地形与森林类型特点,从野外采集的80 个样方中随机选取60 个地形平坦的提取提取波形参数,并将剩余20 个样方用于模型精度评价。绘制波形参数与实测平均树高的散点图,观察其相关性,进而确定平均树高回归模型。
观察图5各参数与实测平均树高散点图可以发现波形后缘长度(TraEdg)和波形前缘长度(LeaEdg)与实测平均树高相关性很弱,波形长度(Extent)与实测平均树高线性关系较为明显。大光斑波形数据进行平均树高反演时,常用波形长度进行估算,本研究结合波形长度(Extent)建立林分平均树高反演模型如式(5)。

式(5)中:a为参数对应系数,b为常量,H为野外实测Lorey's 平均树高,Extent 为波形长度。
2.5 模型评价指标
林分平均树高估测模型拟合相关性采用决定系数R2来评价,其值越大,说明建模精度越好。模型预测精度用P评价,值越大模型预测精度越好,计算方式如式(6)。

式(6)中,P为预测精度,H为野外实测Lorey's平均树高,为林分平均树高反演模型估算值。

图5 实测平均树高与波形参数散点Fig.5 Measured average tree height and waveform parameters scatter plots
3 结果与分析
3.1 波形数据高斯分解
原始波形数据经高斯分解预处理后,结果如图6所示,其中图6(a)为原始波形数据经去噪后检测出的拐点位置及左右拐点的判断,图6(b)为高斯分量的最小二乘波形拟合结果。
图6所示预处理结果表明,研究区机载LiDAR 全波形数据经高斯分解处理流程得到很好的预处理效果。

图6 机载LiDAR 全波形数据预处理Fig.6 Preprocessing of airborne LiDAR full-waveform data
3.2 伪大光斑波形拟合
基于高斯分解方法对样地内所有波形进行分解处理,并将分解后所有高斯分量绘制出来,如图7(a)所示为一个10 m×10 m 样地内的全部波形高斯分量。然后将高斯分量在时间轴上按脉冲能量比例以加权平均的方法进行叠加,拟合形成一条伪大光斑波形数据,即实现了样地内所有波形高斯分量的叠加,进而获得波形参数,结果如图7(b)所示。

图7 伪大光斑波形拟合Fig.7 Pseudo large footprint waveform fitting
激光雷达系统记录波形是按时间先后顺序依次对光斑内各次反射信号数字化采样而成,激光雷达穿透首次回波对应的冠层到达末次回波对应的地面,包含森林垂直结构信息。由此结合图7(b)可以获得伪大光斑波形长度(Extent)。
3.3 模型构建及精度评价
基于伪大光斑波形长度(Extent),建立平均树高回归模型(表3),并结合式(6)对模型进行精度评价,结果如图8所示。

表3 模型及精度评价Table3 Model and accuracy evaluation

图8 验证样方平均树高预测值与实测值Fig.8 Verify sample average tree height predictions and measured values
从模型拟合结果来看,基于伪大光斑所建模型反演精度优于小光斑波形反演精度,本研究的研究区地形相对平坦,研究对象为天然次生白桦林,树干修直,枝叶堆叠较少,通透性好,使得末次回波脉冲能够顺利到达地面而较少地被阻挡,故通过波形长度能够很好地反演林分平均高,且具有较高的可靠性。
分析发现,实测平均树高值与预测值很接近,但也偶有偏差较大的情况,猜测这种现象是因为本研究是对小光斑激光雷达波形数据先波形分解后再形成的伪大光斑波形数据,此过程会有信息的缺失现象,主要是由原始小光斑波形数据预处理(如去噪、平滑)造成且无法避免。具体表现为去噪时噪声阈值过大则会导致有效信息缺失,阈值较小则会使有效波形数据包含过多噪声。平滑时,高斯滤波器选用高斯函数较脉冲宽度小,使估测平均树高略低于实测平均树高。但总体而言,基于伪大光斑波形能够准确反演林分平均高,且精度较波形反演模型有所提高,本研究提出的将样地内所有高斯分量特征参数按脉冲能量比加权平均得到伪大光斑波形数据的叠加方法切实可行。
4 结论与讨论
为了探索小光斑LiDAR 波形数据在估测森林冠层结构参数中的应用潜能,本研究提出形成伪大光斑波形数据的方法,基于小光斑波形数据和伪大光斑波形数据分别建立林分平均高反演模型,并比较分析。结果表明,伪大光斑模型反演精度高于波形反演模型(R2=0.61,P=90.65%)。
研究林分平均高提取方式发现,已有很多运用成熟的遥感技术手段。如:Kodani 等[13]使用LiDAR 在常绿阔叶林林分估计了平均株高,决定系数为0.79;Lin 等[14]建立了平均冠层高度的随机森林回归估计模型,总体平均精度93.17%;胡凯龙等[15]基于GLAS 大光斑波形数据实现林分平均高的提取,相关系数0.66;Fang 等[16]基于GLAS 大光斑波形数据估测山地森林冠层高度,决定系数为82.8%。分析可知,不同遥感技术手段估测林分平均高度的精度较本研究有高有低,研究方法也各有优劣,在应用时需根据实际数据情况选择合适的方法。本研究实现了小光斑机载LiDAR 波形数据估测林分平均树高,将小光斑波形数据拟合成伪大光斑,既弥补了小光斑因光斑过小而易错失树顶信息缺陷,又发挥了小光斑波形数据精确刻画林木特征的优势,在保证精度的同时为定量估测森林冠层结构参数提供了新的方法和思路。
本研究研究对象为天然次生白桦林,样地树种单一,研究区域地形结构相对平坦,对于其他地形区域树种的适用性有待验证。同时基于小光斑机载LiDAR 全波形数据估测林分平均树高时,对波形数据处理效果会在一定程度上影响波形参数的准确提取,而建立林分平均树高估测模型所选取的模型参数波峰长度(PeakLeg)、波形前缘长度(LeaEdg)和波形后缘长度(TraEdg)可直接影响估算结果的精度。脉冲回波信号由于受到大气、航高航速及系统等因素的影响,不可避免地产生大量的噪声,且对于回波信号较弱的波形,有效信号受到噪声的影响往往十分严重,不能有效分离噪声将会影响波形分解的精度甚至产生错误的分解结果。本研究基于高斯分解的方法完成了全波形数据的处理流程,取得了很好的效果,但在采用四分位数方法去噪的过程中,认为对噪声的估计偏大,导致有效波形信息缺失,使模型参数波形前缘长度(LeaEdg)和波形后缘长度(TraEdg)偏小,影响了平均树高的估测精度。在波形平滑处理中,选择了比发射脉冲宽度稍小一点的高斯函数进行滤波,使模型参数波形前缘长度(LeaEdg)偏小,低估了林分平均高度。因此,未来应着眼于波形数据处理方法的改进研究,并尝试扩大研究范围,将该方法应用于复杂地形人工林进行检验,以期在挖掘小光斑激光雷达应用于森林结构参数估测时能够进一步提高估算精度。

