激光切割陶瓷加工过程的数值模拟研究*

赵 婧

(榆林市瀚霆化工技术开发有限公司 陕西 榆林 718100)

前言

激光加工指的是激光束作用于物体表面而引起的物体成形或改性的加工过程[1～2]。以激光作为加工能源，在硬脆性陶瓷加工方面的发展潜力已见端倪[3]：它可以实现无接触式加工，减少了因接触应力对陶瓷带来的损伤；陶瓷对激光具有较高的吸收率(氧化物陶瓷对10.6 μm波长激光的最高吸收率可达80%以上)，聚焦的高能激光束作用于陶瓷局部区域的能量可超过108CJ/cm2，瞬间就可使材料熔化蒸发，实现高效率加工[4]；由于聚焦光斑小，产生的热影响区小，可以达到精密加工的要求。由于陶瓷是由共价键、离子键或2者混合化学键结合的物质，晶体间化学键方向性强，因而具有高硬度和高脆性的本征特性，相对于金属材料，即使是高精密陶瓷，其显微结构均匀度亦较差，严重降低了材料的抗热震性，常温下对剪切应力的变形阻力很大，极易形成裂纹、崩豁甚至于材料碎裂[5]。因此，高效无损伤激光切割陶瓷类高硬脆无机非金属材料一直是一个亟待解决的问题[7～8]。

研究激光与物质热作用过程的理论方法主要有解析法和数值计算法2种。由于涉及到材料熔融和汽化等相变过程的问题非常复杂，理论解析本解比较困难，甚至于根本无法求解。因此一般采用数值方法来处理相关问题。随着计算技术的飞速发展，人们逐渐提出了一些求解激光熔融问题控制方程的新方法，如将激光作用视为点热源、作用对象视为半无限大介质、采用一维近似及假定一个简单的速度场而形成的解析或者半解析法等。而其中的数值计算方法可已采用有限差分法(FDM)和有限单元法(FEM)等，其中有限单元法包含边界元法、有限分析法。对激光与物质相互作用的数值计算就是从特定的物理模型出发，用计算机进行数值计算或模拟，从而揭示激光与物质相互作用的某些性质和运动规律[9]。激光与物质的热作用研究主要是计算激光辐照下物质温度的变化，以及温度变化引起的一些热效应。通常情况下，由于解析或半解析方法必须作一些与实际情况相距甚远的假设，计算结果可能与实际结果有较大偏差，但可作为进一步研究和纯数值计算的基础。主要研究内容如下：

1)描述了Al2O3陶瓷的加热过程，根据经典热传导方程和热应力方程，建立了不同模式激光辐照下中瞬态温度场和热应力场的物理模型，讨论了激光辐射过程中陶瓷温度场及产生的热应力场分布。

2)介绍了激光辐照Al2O3陶瓷的数学模型，利用轴对称的热传导方程和伽辽金法得到了轴对称的有限元的热传导方程，并介绍了空间轴对称物体的温度分布基本理论和有限元解法。

3)计算得到了Al2O3陶瓷在不同模式的激光加热时的温度场以及在施加约束后相应的热应力场，并进行了比较分析。

1 激光辐照材料的温度场理论

激光照射靶材时，其能量被材料表层所吸收并转变为热。该热量通过热传导在靶材内扩散，从而形成温度场，该温度会导致靶材性质的变化。本节将主要对激光加热过程中的热传导现象进行分析和计算，这对激光与材料相互作用的物理机理分析具有重要的意义。激光加载条件、物体形状、初始和边界条件以及物体的热物理性质决定了物体温度场的时空变化。首先给定激光加载条件，通常把被吸收的激光能量或光强作为面热源(表层吸收)或体热源(深层吸收)处理。有时边界上还存在其他种类的热源或冷却条件，如表面辐射损失、气动加热或冷却等。不同介质之间界面的热接触条件比较复杂，理想情况下界面两边的温度和热流量应当相等[17～18]。

由于在物体某处温度达到熔点时，温度暂时不再上升，直到热能达到能够提供继续融化的能量，才能继续融化。这个过程是十分复杂的，在此处不予讨论。只讨论在熔融之前为发生相变时的升温过程。在给定热源、边界和界面条件、初始温度分布和物体的热物理特性时，激光加热各向同性物体的问题就可以归结为不定常热传导方程的计算[19]。

1.1 热导方程与定解条件的理论公式

三维热传导方程可写为如下通用形式：

式中:K——热导率，W·m-1·K-1；

ρ——材料密度，g/cm3；

c——材料比热容，kJ/kg；

T——温度，℃；

t——时间变量，s；

A(x, y, z, t)——每单位时间、单位体积传递热给固体材料的加热速率。

由于材料的热物理系数是温度函数，所以三维热传导方程是非线性的，其解非常复杂，很难得到解析解。然而事实上大部分材料的热物理参数随温度变化并不明显，故在一定条件下可假定其与温度无关，在一定的温度范围内取其平均值进行计算，这样方程(2.1)才可能得到解析解。若激光作用下材料是均匀各向同性的，则三维热传导方程可简化为:

式中：k=K/ρc——材料的热扩散率，m2/s。

由于求解热传导方程非常复杂，许多学者提出了一些热模型，在求解热传导方程时通常的假定条件是[2,19]:

1)被加热材料是各向同性物质。

2)材料的热物理参数与温度无关或取特定的平均值。

3)忽略热传导中的辐射和对流，只考虑材料表面的热传导。

1.2 激光辐照固体材料的理论模型

假定激光束垂直入射于物体表面(即x=0)，被加热物体位于右半空间(x≥0)，物体表面对激光的反射率为R，吸收系数为α，x=0处入射激光束的功率密度(光强)是I0(y,z:T)，则物体内部的温度场T可由热传导方程进行描述:

t>0,x>0

式中：热物理常数ρ,c,k与位置及温度有关； Q是其他体热源项。上式右部是激光束深层吸收的体热源，如果αx≈0或R≈1，用表面吸收率A代替(1-R)，此体热源项可改用边界条件中的面热源表示:

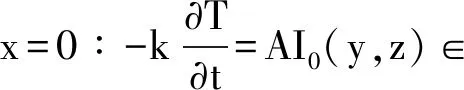
光斑处激光束的强度通常可表示为空间分布I0(y,z)和无量纲时间波形B(t)的乘积。典型的B(t)波形有阶梯波、矩形波、瞬时作用(δ函数)、三角波和梯形波、指数衰减波形、Gauss波形和重复频率波形等。其他面热源以及常用的温度、热流和换热边界条件的提法与普通传热学问题相同。设t=0为激光开始作用的时刻，T0=(x,y,z:0)是给定的初始温度分布。如果初始时物体与环境等温，则热传导方程式计算的是物体的温升△T=T-T0，考虑常温即T0=300 ℃的情况。

考虑被加热物体厚度大于激光脉冲作用时间内热量的传播深度的情况，物体几何形状为圆柱形，表面光斑上的激光强度分布对于光束轴线是旋转对称的，物体的温度场对于x轴也一定是旋转对称的。激光强度呈高斯分布，I=I0(t)exp(-r2/α2)，a是光束的高斯半径，表面吸收，表面反射率和吸收率分别为R和A，时间波形为连续函数B(t)，得到温度场分布为：

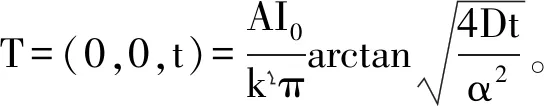
2 激光辐照材料的应力场理论

轴对称物体是指其几何形状中心轴线，则物体内各处的应力外加载荷或温度作用，以及约束情况都对称于某一应变及位移分量也对称于这一轴线。假设物体是连续的线性弹性且是各向均匀同性的，在外力或温度作用下物体的位移和变形是微小的，物体在外加荷载或温度作用之前处于自然状态，内部没有应力存在。

2.1 平衡微分方程

在物体内点P外取一微元六面体PABC，六面体由两个半径差为dr的圆柱面、两个夹角为dθ且包含z轴的垂直面和两个相距为dz的水平面所围成，作用在圆柱面的径向正应力为σr。轴向正应力为σz。圆柱面上的剪应力τrz，环向正应力σθ。

令体力的径向分量为R，体力的轴向分量为Z。将微元体六个面的作用力都投影到半径方向，则

经计算得空间轴对称物体的平衡微分方程为：

2.2 几何方程

在轴对称的物体内每一点只能有2个方向的位移，即沿z轴方向的轴向位移及沿半径:方向的径向位移，由于对称关系，物体内的任一点没有沿圆周方向(环向)的位移。

式中：{ε}——应变列向量；

ur——径向位移，mm；

uz——轴向位移，mm。

2.3 物理方程

由广义虎克定律可得:

将应力分量表示为应变分量的函数为:

式中：μ——泊松比；

E——弹性模量，MPa。

2.4 热弹性方程[20]

对于三维轴对称模型，在忽略体积力和惯性力的前提下，材料体内的温度场发生非均匀变化时产生的热应变和热应力可用如下的热弹性方程来描述:

式中：ur、uz——(r，z)点的位移在r，z方向上的分量；

e——体应变，μm；

β——热膨胀系数，1/k；

E——杨氏模量，MPa；

μ——泊松比。

而应变、应力之间分别满足如下的弹性力学关系式：

e=εr+εz+εθ

对应材料的简支状态，热弹性方程的自由边界条件可取为：

uz|r=a,z=d=0(a为半径，d为高度)

对应于靶材夹紧状态，热弹性方程的固定边界条件可取为：

ur|r=a=uz|r=a=0

2.5 控制方程、初始条件、边界条件[21]

2.5.1 控制方程

假设陶瓷板为各向同性，其热传导方程为[22]:

式中：c，ρ和k分别是陶瓷的质量热容、密度和导热系数；P(x，y，z，t)为体热源的生热率。

2.5.2 初始条件[23]

t=0, T(t)=T0

式中：T0——陶瓷的初始温度，这里视作环境温度300 K。

2.5.3 边界条件

在激光加载面。热传导向陶瓷内部传送的热能，对流换热向外界逸出的热能以及表面向外界辐射的热能，三者之和应该等于其吸收的激光能量，即

αI(x,y,z,t)=

式中：Ts——激光加载面的表面温度，℃；

h——对流传热系数，W/(m2·K)；

ε——表面热辐射系数，W/(m2·℃)；

σ——波尔兹曼常数，J/K；

α——陶瓷对激光的吸收率，%；

I(x，y，z，t)——光能密度，m·W/m2。

在陶瓷板的前后左右和下表面，仅通过对流的方式与外界进行热量交换，因此设置为对流的边界条件[24]，即

式中：∂T/∂n——温度沿表面外法线方向的偏导数；

Tn——玻璃表面的温度，℃。

激光辐射可以看作表面加热源[25]，因此P(x,y,z,t)=0。I(x,y,z,t)为面热源的光能密度，也是激光的功率密度，当激光沿着陶瓷基板的正x轴方向运动时，激光在陶瓷板表面的功率密度可以用函数表示为:

I(x，y，z，t)=I(x-vt，y)δ(z)

则

式中：P0——激光功率，W；

r——激光束半径，mm。

3 不同模式的激光辐照材料的温度场分析

3.1 高斯激光的温度场分析

建立了5 mm×2.5 mm的矩阵模型，为减少计算量，不影响模拟的情况下，划分网格时，为了把更多的计算用于温度变化明显的区域，采用了不等划分方法，在径向分为100份，深度方向分为50份。如图1所示。在计算完结果后可以用ANSYS软件的3D还原功能将其还原，如图2所示。

图1 柱坐标下轴截面的网格划分

图2 柱坐标3D扩展后网格划分效果图

3.1.1 热传导模型

为了便于分析激光与陶瓷相互作用时的温度场，做以下假设：

1)激光束直接作用于材料表面(在材料内没有新的热源)，这是因为激光的照射时间是短暂的。

2)视陶瓷样品表面对激光能量的吸收率为1，且不随时间变化。事实上，吸收系数是根据温度变化而变化的，但是对相同表面的的条件下，测量一个平均值是可行的。

图3 激光照射示意图

3)激光照射期间功率等参数不变。

4)厚板的维度的简化，选择适当的维数进行简化计算，长度，厚度，宽度当到达一定尺度时，可以近似认为无穷大。

5)略热辐射与热对流，认为空气在照射期间是绝热。

6)忽略材料的密度随温度升高的变化。

7)材料是各向同性的。

8)激光束是稳态的。

在有了以上几个假定后，就可以用一般热传到方程求解温度场分布情况了。令激光垂直照射在玻璃板表面。

3.1.2 计算结果温度场分布图及分析

由图4可以看出，在距离加热点一定范围内经过激光辐照过的陶瓷,陶瓷表面(径向)温度传播速度要比陶瓷内部(轴向)要快，超过该范围,温度趋于一致(即环境温度)。中心点最高温度达到1 867 K。

图4功率200 W光斑半径0.5 mm时间步长5 ms高斯激光照射陶瓷界面温度分布图

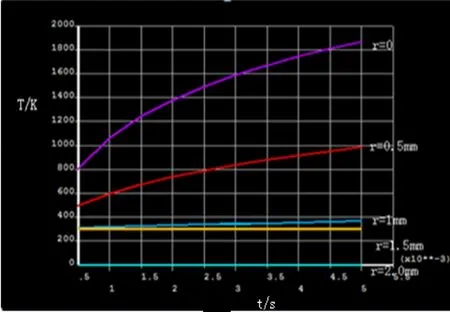
图5径向距离中心原点分别为0、0.5 mm、1.5 mm、2.0 mm随时间温度变化图

图5说明了距离加热中心越近的温度越高且温度上升的速度要比远心点要快。

在径向上，距离加热中心点越近的区域，温度梯度越陡，且梯度随距离的增大而减小，这是由于距离中心点的温度上升速度要比远心点要快，如图6所示。在轴向上的情况基本差不多，但是相比径向，轴向的梯度要比径向要小，且梯度变化相对径向要缓和，如图7所示。

图6 径向温度梯度

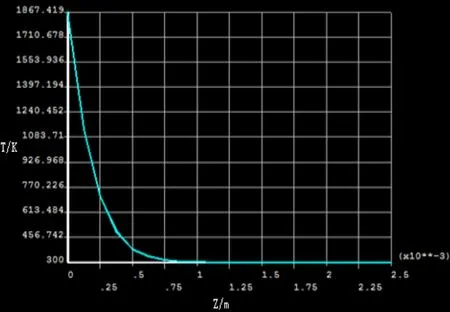
图7 轴向温度梯度

在轴向上，温度梯度要比径向要顺畅，在轴向上各点的温度随时间的增加温度趋势如半S形，如图8所示。

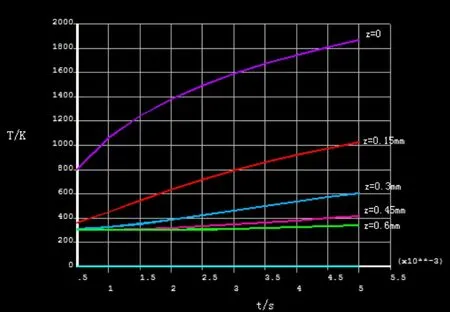
图8 轴向不同深度随时间变化温度图

图9 不同方向上的温度变化

在一定范围内径向温度要比轴向温度高，超出该范围，温度基本一致，即环境温度300 K，如图9所示。

3.2 帽顶形激光的温度场分析

3.2.1 帽顶形激光的载人

激光功率P=200 W 光斑半径r=2.5 mm。

3.2.2 计算结果、温度分布图及分析

图10 帽顶形激光示意图

图11功率200 W光斑半径0.5 mm时间5 ms帽顶形激光照射陶瓷界面温度分布图

相比于图4，帽顶形激光在轴向温度上要比高斯形激光传播要快，中心温度达到2 105 K(假设此时陶瓷没有熔化)。说明中心点的温度要比高斯形激光产生的最高温度要高得多。

一定范围内距离加热中心越近的温度越高且温度上升的速度要比远心点要快。超出该范围，温度基本趋于室温恒定不变，故温度基本无变化。

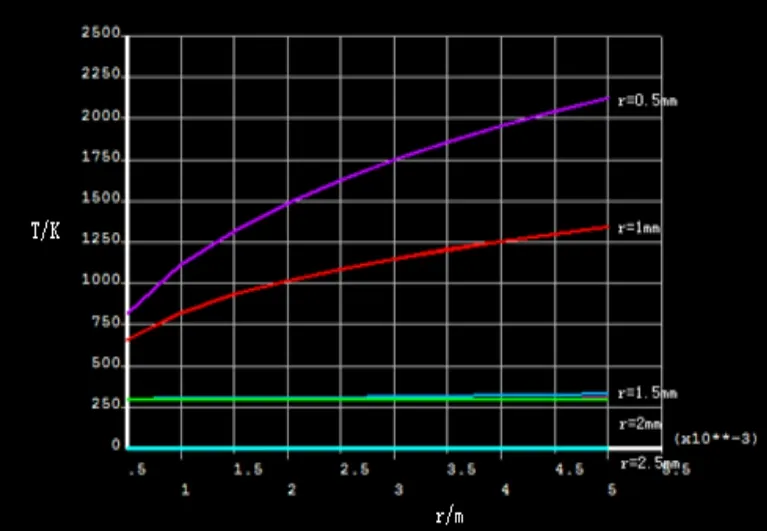
图12径向r=0.5、1.0 mm、1.5 mm、2.0 mm、2.5 mm温度随时间变化图

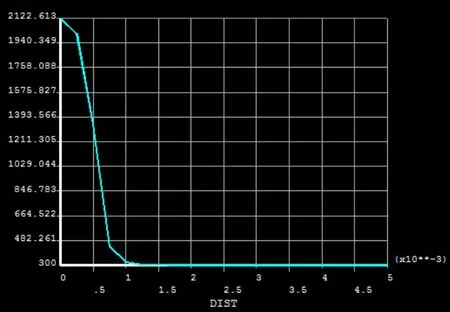
图13 径向温度梯度

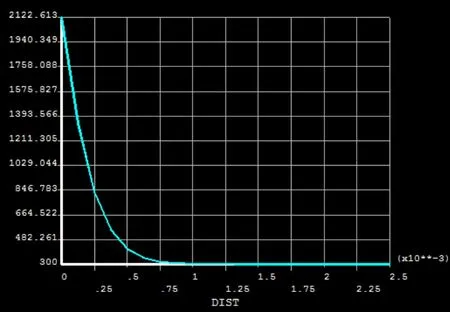
图14 轴向温度梯度

图15 轴向不同深度随时间变化温度变化情况

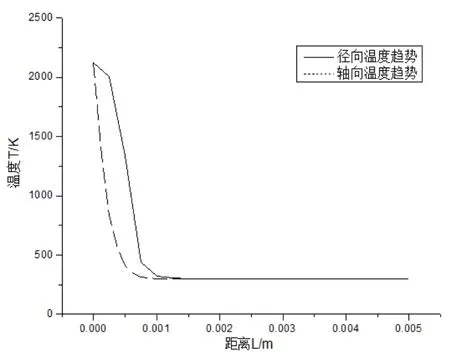
图16 不同方向上的温度趋势

在径向上，距离加热中心点越近的区域，温度梯度越陡，且梯度随距离的增大而减小，也是由于距离中心点的温度上升速度要比远心点要快，如图12所示。在轴向上的情况基本差不多，但是相比径向，轴向的梯度要比径向要小，且梯度变化相对径向要缓和，如图14所示。

由图15可以看出，在一定深度内，各部位的温度变化近似为半S形，且在深度超过0.6 mm后，陶瓷温度基本和环境温度一致(300 K)。

3.3 两种模式的激光产生的温度场的比较

比较在相同的功率、时间步长、光束半径相同的不同模式的激光对同一种模型加热所产生的温度。

3.3.1 径向上的温度比较

在一定的距离内，帽顶形激光的温度传播比高斯形激光传播要快，超过该距离，帽顶形激光要比高斯形激光慢，直到温度不变。不论是何种模式的激光，吸收激光的能量主要分布在光斑半径以内。因此随着时间的增长形成的径向温度梯度也越大。

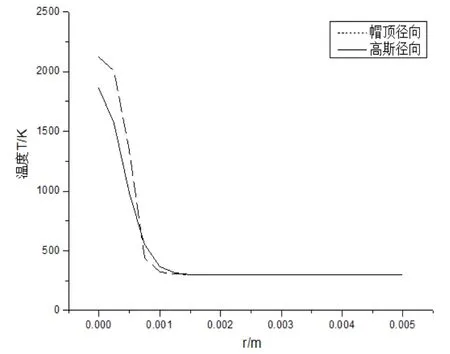
图17 不同模式激光径向温度场比较

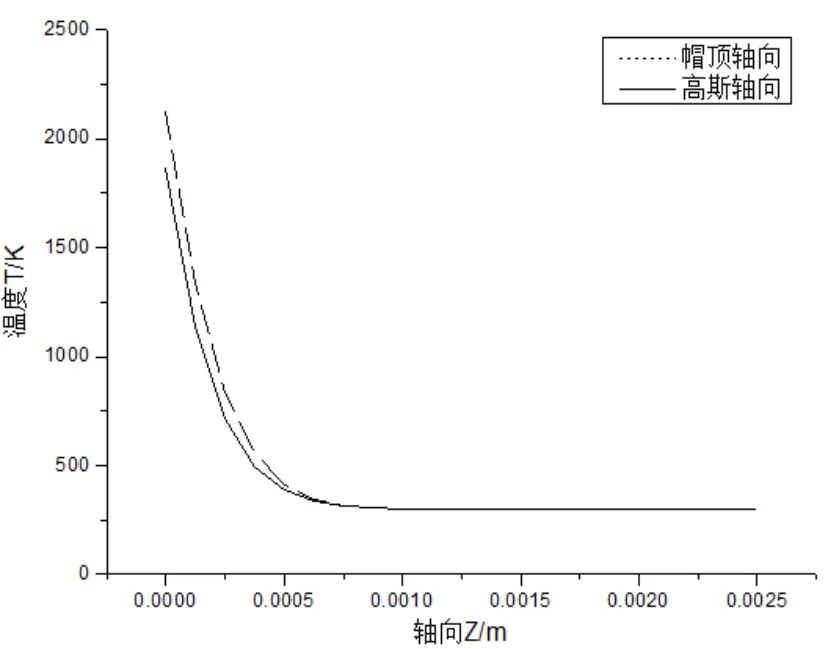
图18 不同模式激光在轴向上的温度比较

3.3.2 轴向上的温度比较

在轴向上，一定范围内，帽顶形激光要比高斯激光温度传播要快。在加热中心点(即光斑半径范围以内)，帽顶形激光产生的温度要比高斯形激光产生的温度要高。

4 激光辐照材料的应力场分析

4.1 模型创建、载入激光

本次模拟建立了20 mm×5 mm×1 mm的长方体模型，用的是一个三维耦合场固体元素SOLID5(该元素有八个节点，每个节点有六个自由度)。并对该模型在长度方向上分了100份，其模型及网格图如图19所示。这次设计模拟的是移动激光束对Al2O3陶瓷基板中心轴线的扫描过程其示意图如图20所示。

图19 应力模拟模型

图20 激光扫描陶瓷基本示意图

相关参数：扫描速度v=2 m/s;时间步长T=10 ms;激光功率=200 W；激光束半径r=0.5 mm。载入激光方程。

4.2 计算应力结果及分析

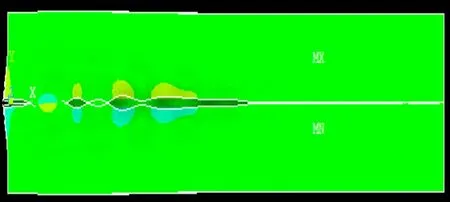
图21 热应力是Y方向产生的位移

热应力总是由于快速的升温或降温所产生的，当热应力超过材料的临界值的时候，材料就会产生断裂。正如本次工作中，材料出现了断裂，如图21所示。

在Y方向上产生的应力随X变化而变化，如图4.4所示，在一定距离内，陶瓷内部产生的是正应力(即应力方向背向陶瓷基板)，超过该距离，内部便产生负应力(应力方向指向陶瓷基板)。过程比较复杂，本次工作不做讨论。

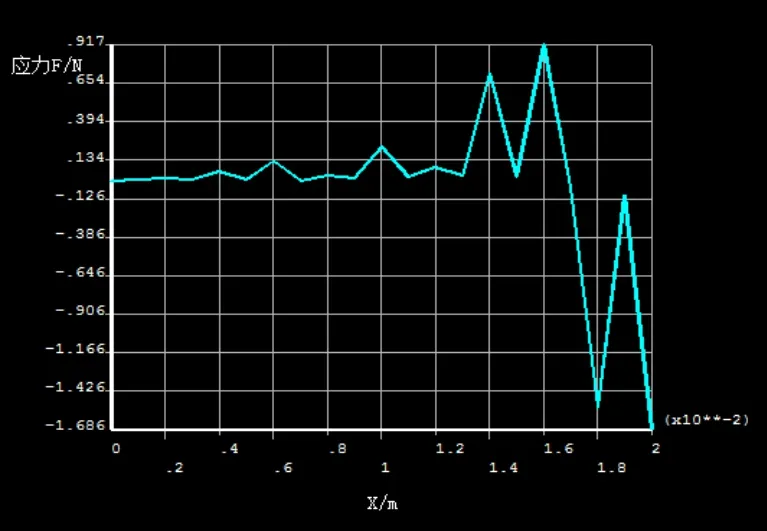
图22 Y方向上的热应力

图23 X方向的温度

图24 等效应力显示

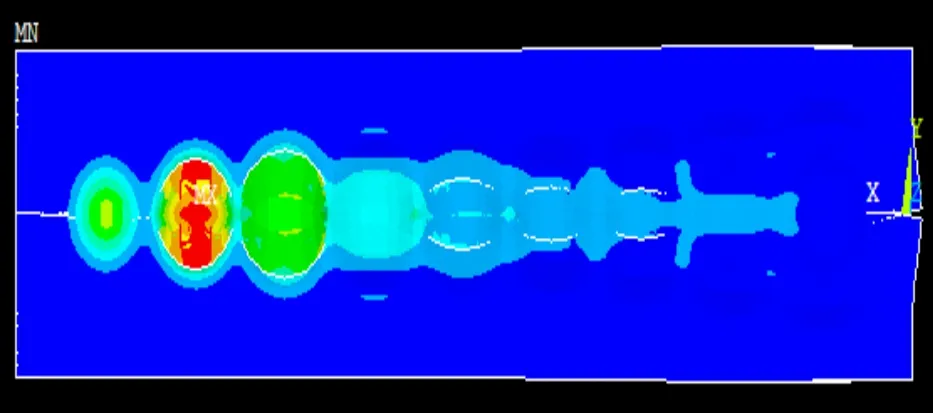
图25 陶瓷基板表面的温度分布

温度变化最快的部分如图23所示，也就是产生断裂的区域，该部位剧烈的热对流产生了超过了陶瓷的临界值，故而产生断裂。

在陶瓷基板上，产生了断裂，最高温度为1 026 K，要远低于熔点2 050 K,之所以断裂，由于陶瓷基板和环境之间的热对流，在陶瓷基板的表面，之前的加热热量也会沿着陶瓷基板的正方方向传播，而导致了最高温度出现在中部，这样会导致陶瓷基本中部很容易出现剧烈的热对流现象，使陶瓷基板的部分区域发生了迅速的升温和降温，从而产生一个极大的应力足够断裂陶瓷基板。如图24和图25所示。

5 结论与展望

在不同模式激光加热陶瓷的过程中，在相同激光功率、加热时间步长、相同环境、模型以及材料的情况下：

在陶瓷基板距加热中心点的一定距离内，在基本表面上，帽顶形激光的温度传播比高斯形激光传播要快，超过该距离，帽顶形激光要比高斯形激光慢，直到温度都接近环境温度。

在陶瓷的轴向方向上，一定范围内，帽顶形激光要比高斯激光温度传播要快，超出该范围，温度都趋于环境温度。

在加热中心点，帽顶形激光产生的温度要比高斯形激光瞬间产生的温度要高。

在激光扫描陶瓷基本的模拟实验中，激光加热可以使陶瓷基板没有达到熔点而出现断裂，断裂一般出现在陶瓷基板的中后部，这是由于热对流的不均匀导致了局部出现了剧烈的升温或降温而产生超过临界值的热应力导致断裂出现。

研究高斯形或者帽顶形激光与Al2O3陶瓷的相互作用过程对激光在工业、军事等各个领域的应用都有非常重要的意义，且作用过程尚有许多问题和工作需要探索、分析和解决。在激光切割陶瓷方面，由于陶瓷本征的硬脆特性 ，使得该技术的发展也存在着许多亟待解决的问题，对陶瓷激光加工的作用机理更需要得到理论上的论证和支持，下面列出一些有待解决的问题和研究内容。

考虑陶瓷表面热对流、热辐射，陶瓷材料的各向异性，热物参数随温度的变化及材料对激光的吸收系数随温度的变化对陶瓷温度场和热应力场的影响。

陶瓷对激光能量的吸收过程中是个复杂的过程，因此不同模式的激光对陶瓷作用时要综合考虑界面吸收、杂质吸收和体吸收。

需要建立更加符合实际的三维模型，根据陶瓷实际情况施加约束条件得到位移分布和应力场分布，并且可以研究应力场随时间的变化，得到激光作用于陶瓷的应力场瞬态变化数据。

研究帽顶形激光加载时可能造成的熔融，气化反应和应力引起的损伤和断裂情况。

可以近一步研究移动激光束对陶瓷作用的温度场和热应力场变化，模拟激光焊接陶瓷过程。

吸收激光的能量主要分布在光斑半径以内，因此随着加热时间增加形成的径向温度梯度也越大。