基于最小二乘支持向量机的汽轮机低压缸排汽焓计算

杨 斌，柳 琦，张 芹，高 原，雷 鸣，余 鹏，何 皓，刘真全

（武汉市政工程设计研究院有限责任公司，武汉 430023）

0 引言

随着智慧能源、智能发电的推广，迫切需要在线计算汽轮机组的经济性，但难于在线计算汽轮机低压缸的排汽焓[1]。低压缸排汽处于湿蒸汽区[2]，需要综合排汽压力、排汽温度和湿蒸汽干度，才能计算其焓。目前低压缸排汽干度无法在线测量[3]，这对在线计算低压缸效率以及汽轮机组的经济性带来了极大挑战[4]。

低压缸排汽焓的在线计算深受科研人员青睐。任浩仁[5]等人利用过热抽汽点拟合做工膨胀线外推在至湿蒸汽获得排汽焓初值，再用热平衡法迭代计算出排气焓，该方法在工况有突变时不太理想。韩中合[6]等人通过进出汽轮机的能量守恒原理来计算汽轮机的排汽焓，该方法需要参数多，计算工作量大。郭江龙[7]等人利用熵增原理来计算低压缸排汽焓，但实用性不大。李慧君[8]等人利用等效焓降来计算低压缸排汽焓，工况有突变时精度差。近年来，随着人工智能的发展，不少科研人员利用机器学习算法来计算汽轮机低压缸的排汽焓，并取得了不少成果。人工神经网络就是一种热门的机器学习算法，但是人工神经网络算法容易陷入局部极值，还易发生“过拟合”现象。

本文通过LSSVM（最小二乘支持向量机）算法来建模计算低压缸排汽焓，LSSVM 不仅能够克服人工神经网络的不足[9]，还能够克服标准支持向量机对于大样本数据训练的局限性，因此被广泛地用于非线性系统的建模中。

1 最小二乘支持向量机

LSSVM 是标准支持向量机在二次损失函数下的一种表现形式，其等式约束代替了不等式约束，将二次规划问题转变为一组等式方程来求解，缩短了求解所耗时间，有效地解决了大样本数据学习和训练的问题[10]。

1.1 回归预测原理

LSSVM 的预测原理如下[11]，对于样本集：

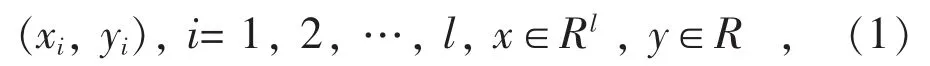
式中：xi表示第i 个输入向量；yi表示第i 个输出。

LSSVM 的回归模型为[12]：

式中：H 和n 为需要确定的参数；φ（·）为非线性映射。

将样本映射到特征空间中，求解式（3）的最小化即可确定H 和n，式（3）的最优化问题可以表示为式（4）的形式：

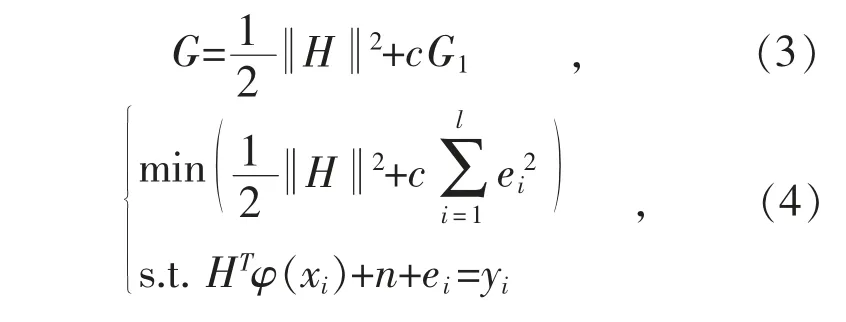
式中：G1表示损失函数；c 表示调节因子，i=1，2，…，l。

与式（4）相对应的Lagrange 函数为：

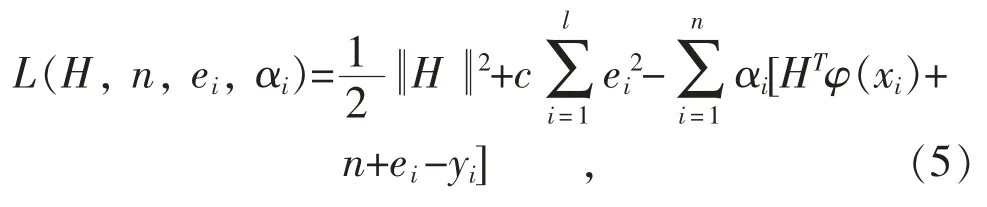
式中：αi≥0 表示Lagrange 乘子；ei表示误差。根据KKT 条件：

即可得到式（6），消去H 和ei后，最终得到回归函数如式（7）所示：

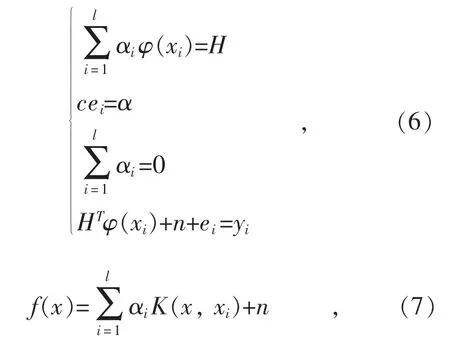
式中：K（x，xi）=φ（x）Tφ（xi）为一个满足Mercer 条件的核函数。核函数是影响LSSVM 模型性能的关键。

1.2 核函数

LSSVM 常用的核函数通常有线性函数、多项式核函数和径向基函数等。其中，径向基函数因其较宽的收敛域和较强的泛化能力[13]，被广泛应用于回归分析中，本文是用LSSVM 进行非线性系统建模，因此选径向基函数作为核函数，其表达式为：

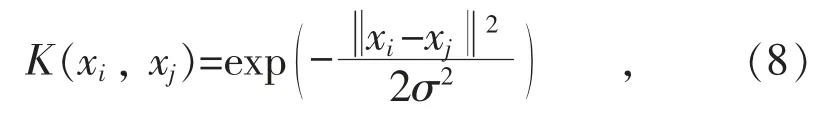
式中：σ2表示核宽度。该核函数用于最小二乘支持向量回归分析时，调节因子c 和核参数σ2是影响性能的2 个超参数[14-16]，因此这2 个参数设置显得至关重要。

2 排汽焓计算模型

基于进出汽轮机能量守恒的原理，本文着重分析影响汽轮机排汽焓的因素，经分析温度、压力、流量参数是影响汽轮机能量平衡的重要参数。LSSVM 模型的输入变量为：机组负荷，主蒸汽流量、压力和温度，调节级后以及中压缸进汽压力和温度，高压缸排汽以及低压缸排汽压力和温度，八级抽汽压力和温度，总计28 个参数[17]。LSSVM 模型的输出变量为：汽轮机低压缸排汽焓。采集到的历史数据经过预处理后再进行归一化，最后对LSSVM 模型进行训练，再用性能试验的数据来对模型进行验证，其计算流程如图1所示。

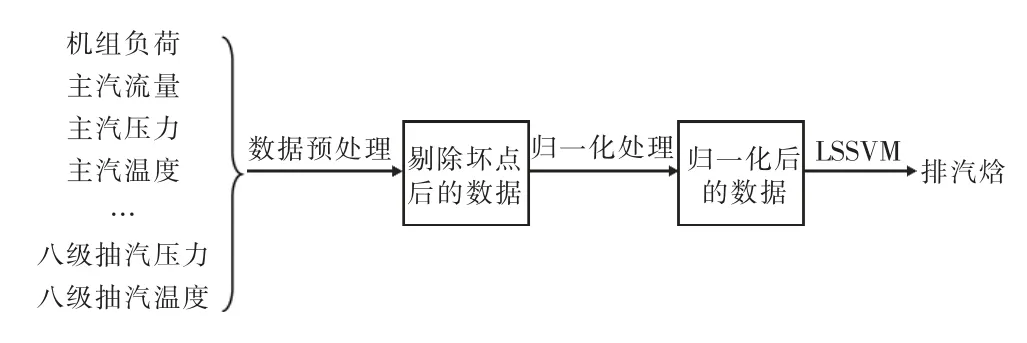
图1 基于LSSVM 模型的汽轮机低压缸排汽焓计算模型

2.1 数据预处理

机组热工参数测量偶尔存在坏点，必须要先剔除，才能用于训练LSSVM 模型。本文采用的数据预处理方法为证实法[17-18]，用五阶不加权计算模型，计算系数矩阵为B=（0.41，0.06，-0.37，0.37，0.53）。当测量值偏离计算值超过20%时，就用计算值代替测量值。

计算模型如下：

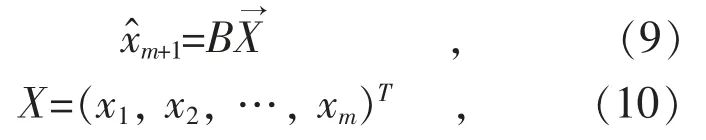
式中：xm+1为数据预处理计算值；xm为前m 个测量值；X 为原始测量值矩阵；B 为计算系数矩阵；T 为矩阵转置运算。

2.2 归一化原理

机组负荷、流量、压力、温度、排汽焓等参数的单位不一致，且数量级及量纲差异大，影响对LSSVM 模型训练。归一化处理可以消除这一影响[19-20]，归一化公式为：

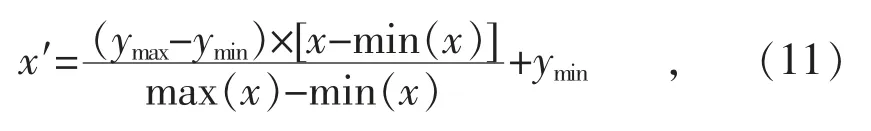
式中：x 为输入值；x′为输出值；ymax为统计范围内最大值；ymin为统计范围内最小值。归一化后的所有参数均是-1～1 的无量纲量[17]。

3 实例计算

对某在役的300 MW 亚临界双缸双排汽汽轮机组进行计算。该汽轮机组经过大修之后一直运行良好，采集一段时间内LSSVM 模型需要的所有负荷工况下的数据。由于数据组数多且量大，不便于逐一展示，此处仅展示部分主汽温度数据，如图2 所示[17，21]。

由图2 可知，历史数据中存在一些极大极小的坏点，不利于训练LSSVM 模型，需要剔除。由图3 可知，数据预处理后剔除了极大极小的坏值点。对LSSVM 模型的输入参数与输出参数均进行数据预处理，以利于训练LSSVM 模型[21]。

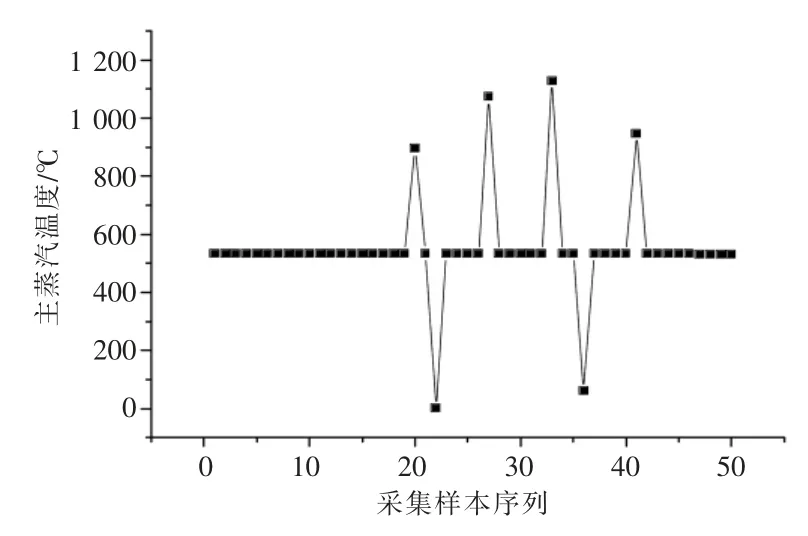
图2 数据预处理前部分主汽温度分布

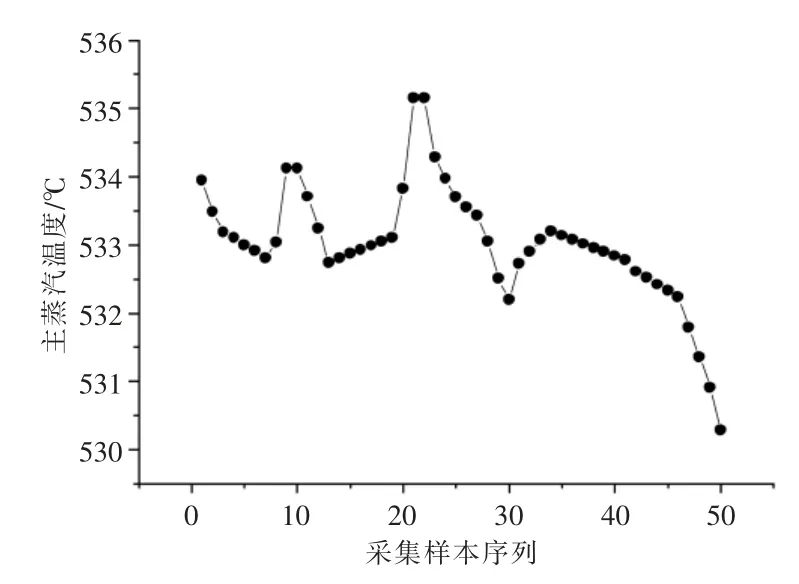
图3 数据预处理后部分主汽温度分布

3.1 模型训练

随机抽取2 000 组数据作为训练样本数据，用以训练LSSVM 模型，再用200 组性能试验数据作为验证样本数据，用以验证模型训练的效果，部分训练样本数据如表1 所示。

表1 部分训练样本数据

由于采集到的历史数据的量纲并不一致，数量级也不一致，为了消除量纲和数量级对模型训练的影响，首先对剔除坏点后的所有历史数据做归一化处理，由于数据组数太多，本文仅列出主汽流量、主汽温度与机组负荷归一化前后的数据来对比分析，如图4—7 所示。

图4 归一化前主汽流量与机组负荷关系

由图4 知，归一化前主汽流量在400～1 000 t/h变化，机组负荷在100～300 MW 变化，主汽流量与机组负荷数值相差较大，但其变化趋势相似，经过归一化处理后，主汽流量与机组负荷均变为无量纲量且在-1～1 的区间内变化，并保持着原来的变化趋势，因其变化趋势相似，归一化后又都在-1～1 的区间内，主汽流量与机组负荷归一化后变化曲线几乎重合，如图5 所示。

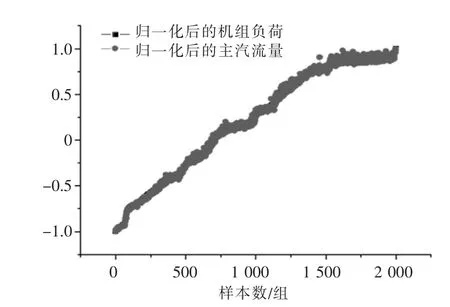
图5 归一化后主汽流量与机组负荷关系

由图6 知，归一化前主汽温度在500～550 ℃变化，机组负荷在100～300 MW 变化，主汽温度与机组负荷数值相差较大，主汽温度几乎保持平稳波动，机组负荷在逐步变大，主汽温度和机组负荷的变化趋势并不一致。经过归一化处理后，主汽流量与机组负荷均变为无量纲量并且在-1～1 的区间内变化，仍保持原来的变化趋势，如图7 所示。

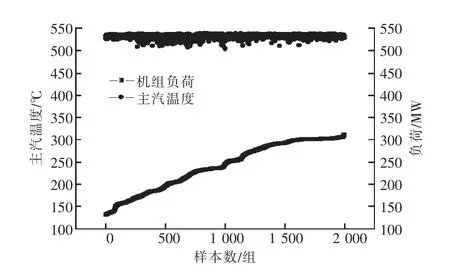
图6 归一化前主汽温度与机组负荷关系

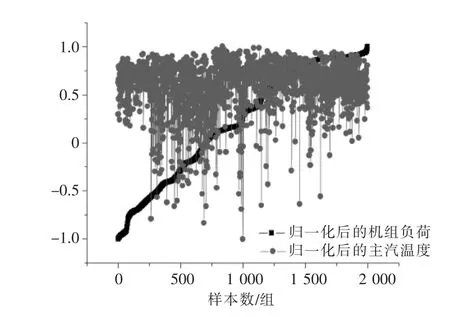
图7 归一化后主汽温度与机组负荷关系

经过归一化后的数据用于LSSVM 模型的训练，LSSVM 模型的核函数选用RBF 径向核函数，初步设定调节因子c 为136、核参数σ2为8，LSSVM 模型经过训练后，最终得到优化的调节因子c 为389.57、核参数σ2为13.85。

3.2 模型验证

验证样本数据代入训练好LSSVM 的模型后得到排汽焓的预测值，部分预测值如表2 所示。

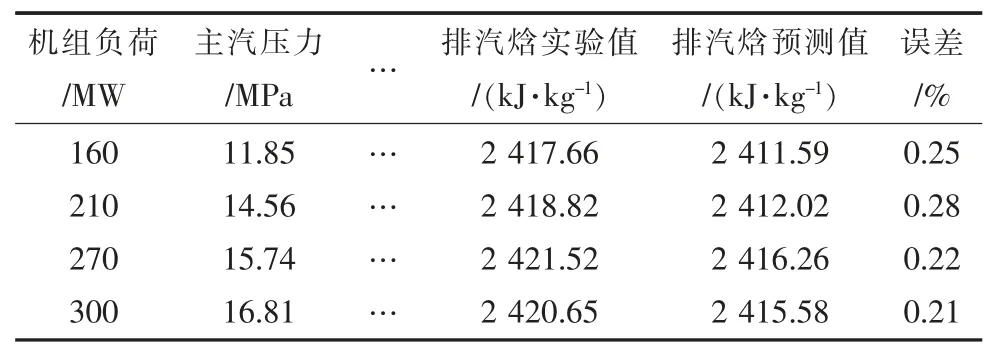
表2 部分验证样本数据

由表2 可知，基于LSSVM 模型的排汽焓预测值精度高，在各种工况以及变工况下，相对误差绝对值都在1%以内，满足工程应用。本文着重分析排汽焓的试验值与机组负荷之间的关系、排汽焓的预测值与机组负荷之间的关系、排汽焓的预测值与试验值之间的关系，分别如图8—10所示。

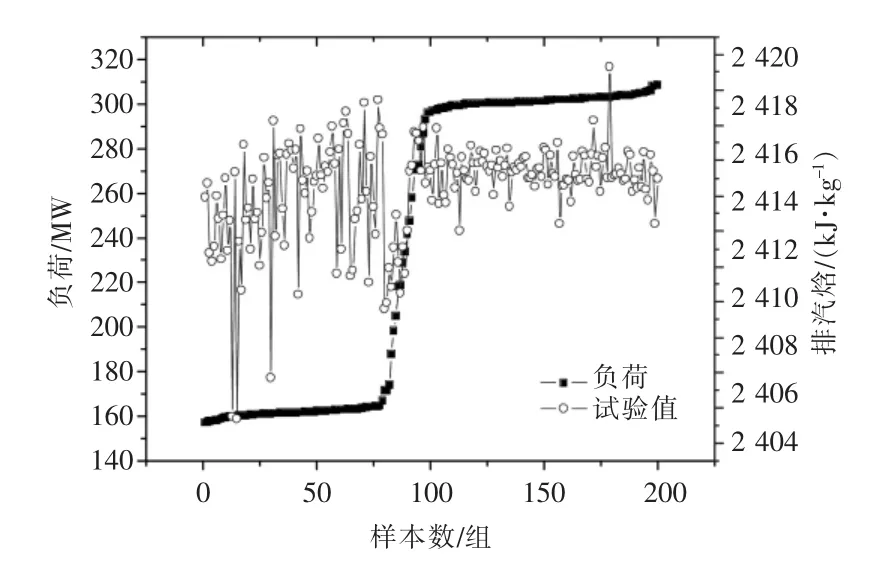
图8 低压缸排汽焓试验值与机组负荷关系

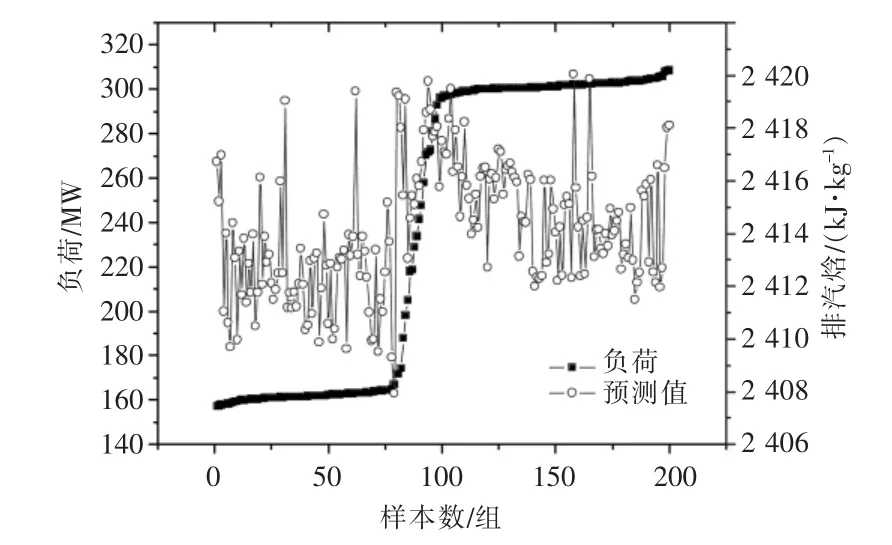
图9 低压缸排汽焓预测值与机组负荷关系

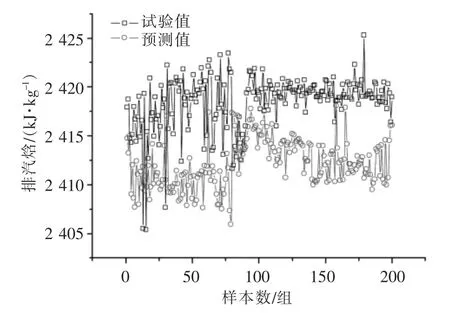
图10 低压缸排汽焓试验值与预测值关系

由图8 可知，汽轮机机组在50%负荷工况左右时，排汽焓的试验值波动较大，这是由于负荷较低时机组参数不稳定造成的。汽轮机机组在90%负荷工况左右时，排汽焓的试验值相对较稳定，汽轮机机组负荷由低到高上升时，排汽焓整体保持上升，但幅度不大。在50%～100%负荷工况下，低压缸的排汽焓都在2 404～2 426 kJ/kg 波动，波动幅度在22 kJ/kg 范围内[22-23]。

由图9 可知，排汽焓的预测值和试验值随着负荷的变化规律相似。负荷低时，排汽焓波动较大，负荷高时排汽焓波动相对较小，排汽焓随负荷升高而整体略上升。在50%～100%负荷工况范围内，排汽焓的预测值在2 404～2 420 kJ/kg 波动，波动幅度在16 kJ/kg 范围内。

进一步分析图10 可以看出，排汽焓的预测值整体上都比试验值小约5 kJ/kg，相对误差小于1%，在工程上可以对预测值进行适当修正，可见基于LSSVM 的汽轮机低压缸排汽焓的预测值可以进行工程应用。

4 结论

本文利用机器学习算法LSSVM，建立了基于LSSVM 的汽轮机低压缸排汽焓计算模型，将进出汽轮机的流量、温度、压力以及机组负荷等参数作为输入变量，低压缸排汽焓作为输出变量，建立LSSVM 模型，用大量样本数据对模型进行训练后，储存于计算机中，在线计算汽轮机经济性时可以实时调用该模型。该模型具有以下优点：

（1）实现了机器学习算法LSSVM 对汽轮机低压缸排汽焓的在线计算，而且不用考虑门杆及轴封漏汽带来的计算误差，计算量小。

（2）LSSVM 避免了神经网络的“过拟合”现象，克服了普通支持向量机对大样本数据训练的局限性。

（3）机组变工况下，汽轮机低压缸排汽焓的计算误差均在1%以内，符合工程要求。

本文排汽焓计算模型是基于LSSVM 的在线计算，如何对LSSVM 模型进行优化还需进一步研究。