变电站二次直流失电保护系统的可靠性分析

王幸主，戚宣威，王 松，宣晓华，陆承宇，文明浩

（1.华中科技大学，武汉 430072；2.国网浙江省电力有限公司电力科学研究院，杭州 310014）

0 引言

继电保护作为保障电力系统安全稳定运行的第一道防线，其正常工作的前提条件是变电站二次直流电源可靠地为其供电[1-2]。一旦变电站发生二次直流电源消失的情况，且此时系统又发生了故障，则该变电站的所有保护装置均无法正常工作，只能依靠相邻变电站的远后备保护来切除故障。这样不仅大大延长故障切除时间，而且对于远后备保护整定困难的相邻站来说，其保护动作的灵敏性和可靠性也大大降低[3-5]。

随着计算机技术和光纤通信技术的发展，以及IEC 61850 标准的实施[6-7]，相关学者提出了针对变电站二次直流失电的保护系统[8-9]。但是目前并没有研究对提出的失电保护系统进行定量的可靠性分析，因此其可靠性无法验证。针对传统继电保护系统的可靠性评估，相关文献已经进行了大量的研究，提出了一系列可靠性评估方法[10-14]。文献[10]提出了一种基于GO 法的继电保护系统可靠性分析方法，但是GO 法操作符类型多且使用复杂，不仅要求对继电保护系统原理非常熟悉，而且对GO 法也要有足够的理解，使用起来有一定的难度。文献[11]提出了一种基于Markov 状态空间法的继电保护系统可靠性分析方法，但是存在状态空间“组合爆炸”的问题，不适用于大型复杂系统的可靠性分析。文献[12]对传统Markov 状态空间法进行了改进，对依据保护逻辑建立的Markov 状态空间进行了模糊化处理，但是仍存在状态空间组合复杂的问题。文献[13]提出了基于蒙特卡罗模拟法的电力系统可靠性评估方法，随机模拟的次数与系统规模无关，适合对复杂系统进行可靠性的定量计算，但是计算精度有待进一步提高。文献[14]基于可靠性框图法对数字化继电保护系统进行了可靠性评估并分析了薄弱环节，但是可靠性框图法是一种静态的建模和分析方法，难以描述系统部件之间存在的动态关系。

本文以失电保护系统为研究对象，建立了变电站二次直流失电保护系统各个环节的可靠性分析模型。采用基于故障树的序贯蒙特卡罗算法分析其可靠性，并给出可靠性指标，为失电保护系统的评价和改进提供一种定量的分析方法。

1 失电保护系统的拓扑结构

假设系统结构如图1 所示，变电站C 发生二次直流失电。

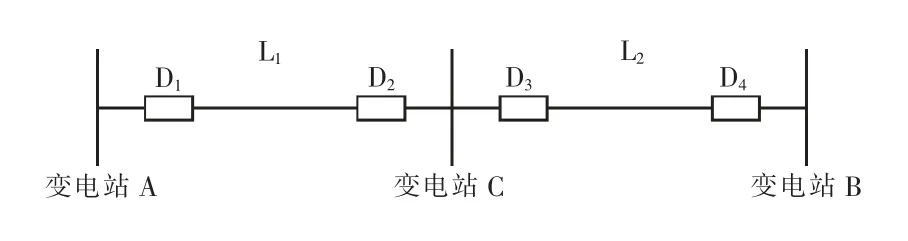
图1 系统结构

根据目前变电站二次回路的设计规范，保护装置的直流电源和通信电源相互独立。基于此，文献[3]提出了一种失电保护系统，其站内接线如图2 所示。

当变电站C 发生二次直流失电时，其站内的48 V 通信电源仍保持正常工作状态，以保障MCD（失电检测装置）检测到失电信息并发送失电信息给所有相邻的变电站，然后相邻变电站再结合本站检测到的电气量进行故障判断。综合考虑失电保护装置所需要的采样、跳闸、失电检测等环节，则变电站二次直流失电保护系统的结构如图3 所示。

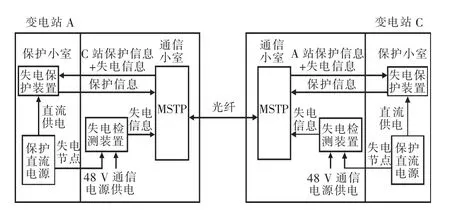
图2 变电站站内接线

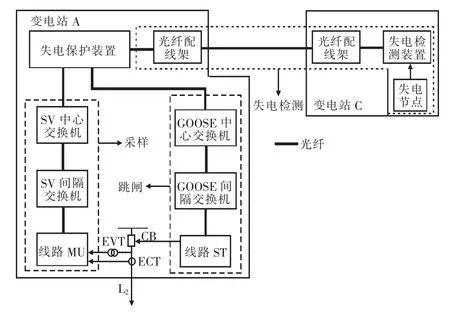
图3 失电保护系统拓扑结构

2 失电保护系统的可靠性模型

根据故障树分析法的符号规则[15]，下述可靠性模型中各个符号的分类和名称如表1 所示。此外，在传统的继电保护系统可靠性评估中，根据继电保护的动作特性，保护系统的失效类型分为拒动失效和误动失效，以下分析中也分为这两类。

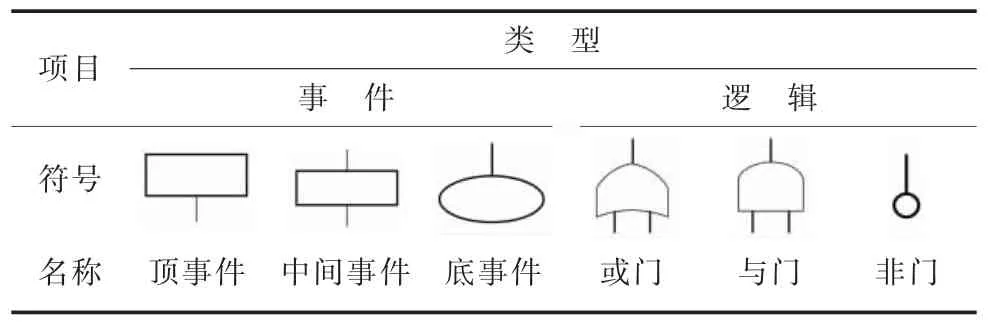
表1 故障树事件和逻辑符号

2.1 失电保护系统整体

根据故障树分析法，结合图3 所示的失电保护系统拓扑结构，建立失电保护系统的整体可靠性模型如图4 所示。其中，失电保护系统的误动失效主要包括2 种情况：跳闸回路发生误动失效；跳闸回路正常情况下失电保护装置发生误动失效。失电保护系统的拒动失效情况与误动失效类似，不再赘述。

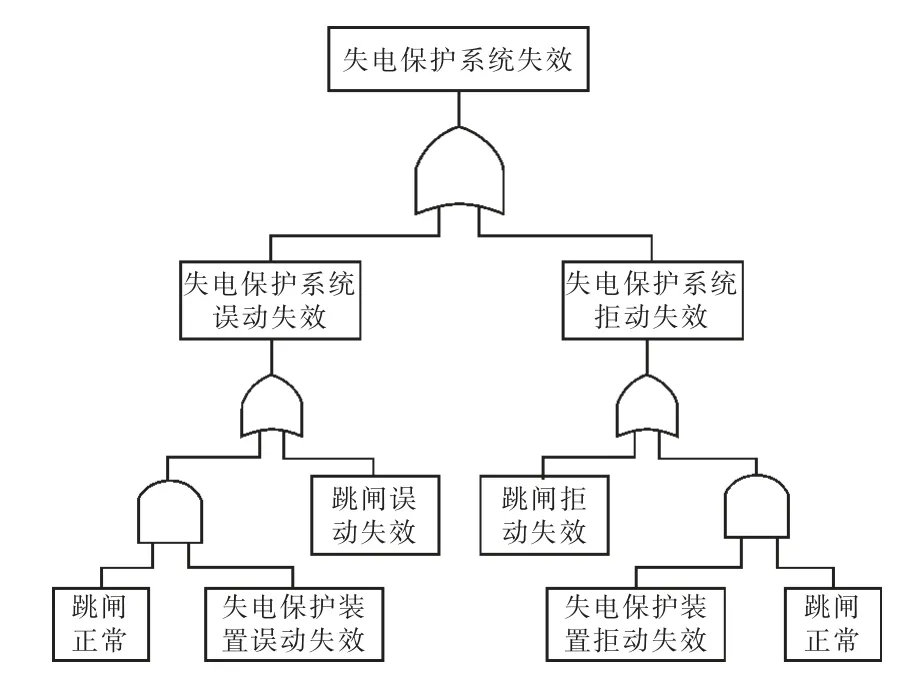
图4 失电保护系统整体可靠性模型

下面进一步分析图4 中的中间事件，直至各个底事件为止。

2.2 跳闸

从图3 所示的失电保护系统的拓扑结构可以看出，跳闸环节主要包括GOOSE 通信网络、CB和ST 等部分。因此，跳闸误动失效包括2 种情况：CB 本身发生误动失效；在CB 正常的情况下，ST 发生误动失效。跳闸拒动失效包括3 种情况：CB 本身发生拒动失效；ST 和CB 正常情况下GOOSE 网络失效，无法发送失电保护装置的跳令至ST；CB 正常情况下，ST 本身发生拒动失效。据此可得到跳闸环节的可靠性模型如图5 所示。

2.3 通信网络

从图3 可以看出，整个失电保护系统通信网络包括3 部分，分别是：SV 通信，把采样信息发送至失电保护装置；GOOSE 通信，发送失电保护装置的跳闸命令至ST；失电检测通信，把失电站的失电信息发送至与之相邻的变电站。其中SV和GOOSE 通信网络结构类似，都由OP（光纤）、SW（间隔交换机）、中心交换机等部件组成。当SV和GOOSE 通信网络中任一部件出现问题时，整个通信网络就发生了失效。因此，SV 和GOOSE通信网络的可靠性模型如图6 所示。

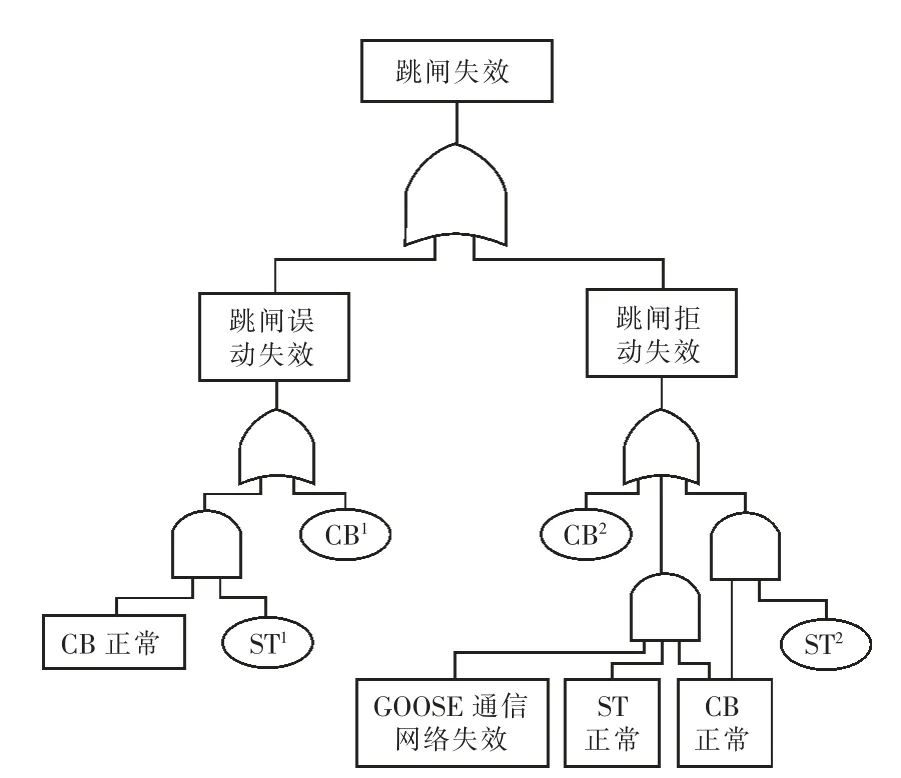
图5 跳闸环节的可靠性模型

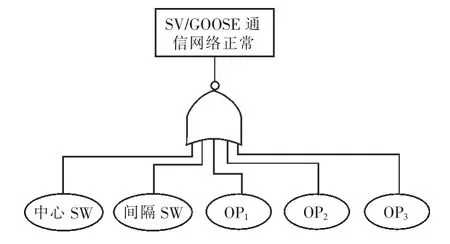
图6 SV/GOOSE 通信网络的可靠性模型

把图6 中SV 和GOOSE 通信网络结构中的SW 换成ODF（光纤配线架），即可得到失电检测通信网络的可靠性模型。

2.4 失电保护装置

参考传统继电保护装置本体的可靠性模型[16]，并结合失电保护装置自身的特点，建立失电保护装置误动失效和拒动失效的可靠性模型如图7 所示。图7 中MEM，CU，PSU，QD，ACT 分别为存储、通信、电源、启动、算法等部件。

2.4.1 失电检测

从图3 可以看出，失电检测环节包括通信电源、MCD 以及失电检测通信网络3 部分。对于失电检测误动失效来说，需要满足失电检测通信网络和通信电源正常，并且MCD 发生误发失电信息的故障。而对于失电检测拒动失效来说，失电检测环节任一部件发生拒动失效均会导致失电检测环节发生拒动失效。因此，失电检测环节的可靠性模型如图8 所示。

2.4.2 采样

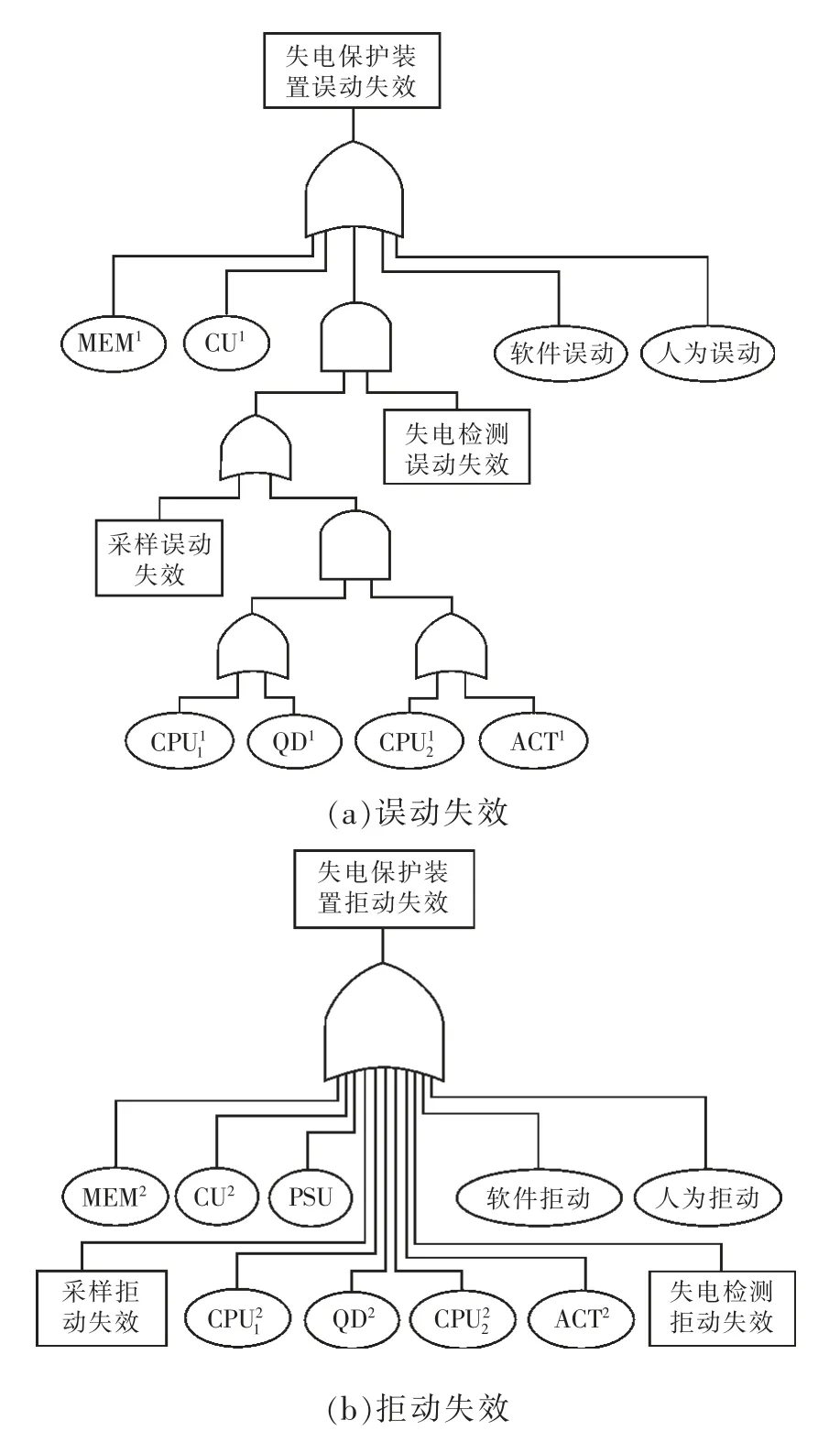
图7 失电保护装置可靠性模型

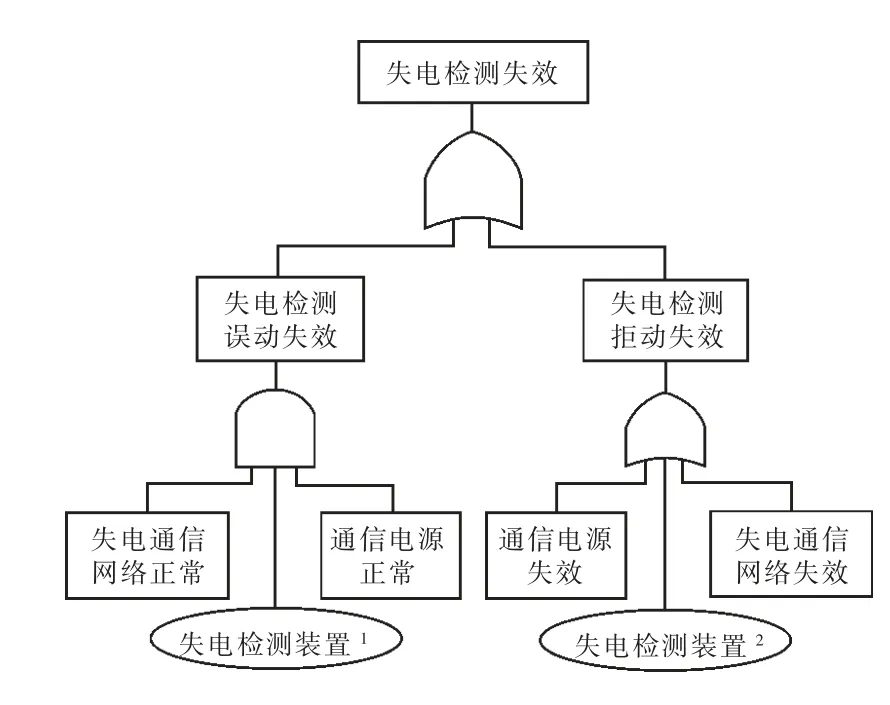
图8 失电检测环节可靠性模型

采样环节可靠性的分析与2.2 节中跳闸环节可靠性分析类似。需要注意的是，由于信息流向的不同，对于采样误动失效来说，需要满足SV通信网络正常，这样才能把MU，ECT 及EVT 的误动失效信息发送至失电保护装置。因此，采样环节的可靠性模型如图9 所示。

图9 采样环节可靠性模型

3 可靠性指标

3.1 平均无故障工作时间和平均修复时间

MTBF（平均无故障工作时间）和MTTR（平均修复时间）分别反映系统或者部件在整个生命周期过程中平均两次故障之间的时间间隔和平均修复每次故障所需要的时间。

3.2 可用度

可用度表示系统或者部件在起始时刻完好的条件下，在时间区间[0，t）内不发生失效的概率，用来评估系统或者部件长期运行的可靠性水平。定义为：

3.3 概率重要度

概率重要度用来定量地衡量各底事件发生概率的增减程度对顶事件发生概率的影响尺度，可用来确定每个底事件对系统整体的重要程度，发现系统的薄弱环节，为提高系统的可靠性提出合理建议。其定义为：

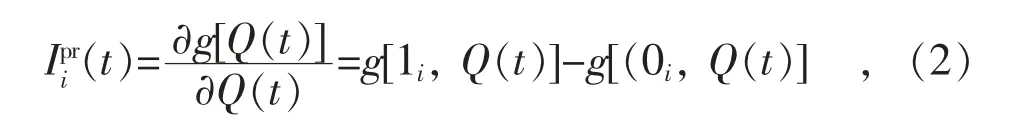
式中：Q（t）为系统的不可用度；g[Q（t）]为系统的失效率；i 表示对应部件的编号。

由式（2）可知，部件的概率重要度就是底事件状态取1 时（底事件发生）系统失效率和底事件状态取0 时（底事件未发生）系统失效率之差。

4 仿真结果

根据图4—图9 建立的变电站二次直流失电保护系统的可靠性分析模型，采用基于故障树的序贯蒙特卡罗算法进行可靠性评估。其中保护装置各部件的失效率参数分别为[16]：λMEM=λCPU=36.738×10-6，λCU=22.562×10-6，λPSU=11.4×10-6，λQD=7×10-6，λACT=λ软件=7.504×10-6，λ人为=4×10-6；除软件的修复率为1/48 外，其他部件修复率参数均为1/24。其他设备的失效率和修复率参数如表2所示。假设所有部件的MTBF 和MTTR 均服从单参数的指数分布，且误动失效率和拒动失效率各占部件失效率的1/2。

表2 部分设备失效率和修复率

取最大仿真时间为106h，经过多次仿真，当可靠性指标收敛后进行统计。

4.1 失电保护系统的可靠性指标

经过仿真计算，图3 所示变电站二次直流失电保护系统的MTBF，MTTR 及可用度等可靠性指标如表3 所示。

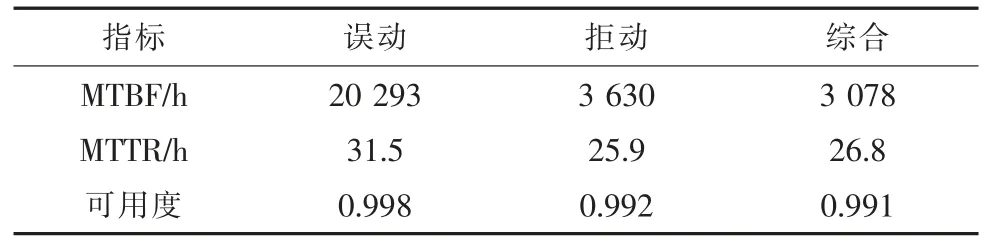
表3 失电保护系统的MTBF，MTTR，可用度

从表3 分析可得，失电保护系统的误动MTBF远大于拒动MTBF，这主要是由于失电检测部分任一部件拒动失效均会导致失电保护系统发生拒动失效。然而误动失效发生的条件则要苛刻得多，需要同时满足失电检测通信网络和通信电源正常，并且MCD 误发失电信息。下面的部件概率重要度分析也说明了这一点。此外，不论是误动失效还是拒动失效，失电保护系统的可用度都是比较高的。

对于失电保护系统来说，它与传统保护系统的主要区别在于失电检测，因此下面只分析了失电检测部件的概率重要度，结果如表4 所示。

表4 失电检测部件的概率重要度

从表4 分析可得，相比于失电检测部件的拒动概率重要度，其误动概率重要度要小得多。对于失电保护系统误动来说，提高失电检测保护装置的误动可靠性可有效降低失电保护系统发生误动失效的概率。而对于拒动来说，失电检测通信网络部件、通信电源以及失电保护检测装置对拒动可靠性的影响都比较大，据此可以提出针对性的改进措施。

4.2 改进措施

根据4.1 中的仿真结果，下面对图3 所示的失电保护系统结构提出改进措施，即分别双重化配置失电保护装置和失电检测通信网络，并进行仿真验证。改进以后失电保护系统的MTBF 如表5 所示。

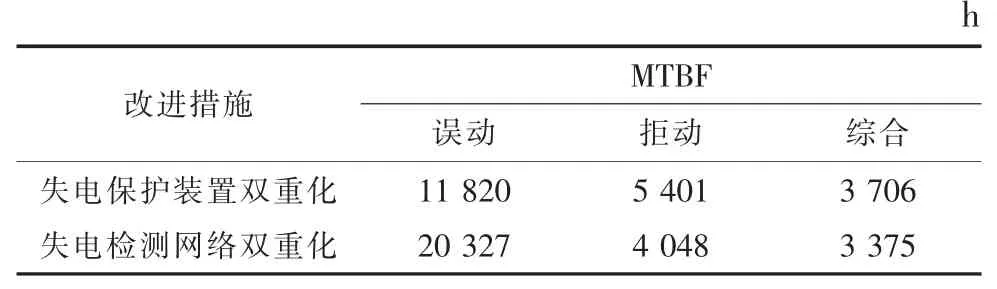
表5 改进后失电保护系统的MTBF

相比于表3，由于失电保护装置双重化配置后2 台保护装置任意1 台误动都会造成失电保护系统误动，而2 台保护装置同时拒动才会使失电保护系统拒动，因此，表5 中误动的MTBF 降低，但是拒动的MTBF 明显增加，而且整体的MTBF也是增加的。此外，由于失电检测部件误动的概率重要度很小，因此失电检测通信网络双重化配置以后对失电保护系统误动的MTBF 影响不大，但是明显提升拒动和整体的MTBF。

综上，为了进一步提高变电站二次直流失电保护系统的可靠性，可以考虑双重化配置失电保护装置和失电检测通信网络。

5 结语

为了定量评估变电站二次直流失电保护系统系统的可靠性，首先根据故障树分析理论和失电保护系统的工作机制，对失电保护系统的采样、跳闸、通信、失电检测以及失电保护装置等环节分别进行可靠性建模。然后利用序贯蒙特卡罗算法对失电保护系统进行仿真，得出MTBF、可用度以及部件概率重要度等可靠性指标。相关指标表明，失电保护系统的可用度是非常高的，但是失电检测通信网络是失电保护系统的薄弱环节。最后，根据仿真结果针对性地提出了失电保护装置和失电检测通信网络双重化等措施，经验证相关措施可以进一步提高失电保护系统的可靠性。