基于改良SEIR模型的微信谣言传播研究

刘本莹，罗 勇，黄忠乾

(温州大学数理与电子信息工程学院，浙江温州 325035)

微信作为移动社交网络的行业翘楚，其发展至今，已超越了传统意义上的社交工具属性，成为了兼具媒体特质的沟通平台与表达渠道，对人际交流及媒体变革产生了广泛而深远的影响.由于微信的功能、用户数量的庞大及信息传播封闭等特点，一些别有用心的人出于各种目的，利用微信平台，制造大量的伪科学甚至荒唐的谎言、谣言以及低俗无趣、蛊惑人心的言论、图片、视频进行传播，一时间难以发现并得以甄别，它利用朋友间建立起的信任，广泛、迅速地传播，速度惊人，不仅会影响大众正常视听，还会造成一定范围内的社会恐慌，使微信不可避免地成为了一个谣言传播的网络阵地.

微信谣言传播与传染病传播有诸多相似之处，因此国内外许多学者都借助生物数学中的传染病模型来研究网络谣言，其中较为典型的传染病模型有SI模型、SIS模型[1]、SIR模型[2]、SEIR模型[3].诸多学者在此基础上做了很多尝试.2001年，Zhao等人[4]首次将SIR模型应用于在线社交博客平台.2002年，Zanette[5]研究了小世界网络中的谣言传播模型，并得到传播阈值，为谣言传播模型的研究奠定了基础.2008年，Gu等人[6]在经典谣言传播模型中考虑了记忆和遗忘机制，并详细分析了这两种状态下对谣言传播过程的影响.随着移动社交网络的兴起，朱海涛等人[7-9]改进SEIR模型，通过传播阈值的机理分析提出相应的建议并对其进行仿真，验证了模型的准确性.

本文以经典的传染病模型为基础，考虑到微信用户数量持续增长，谣言传播速度较快，而由于微信的熟人社交属性，许多人爱面子或无视辟谣信息、正确信息传播闭塞的特点，应用由双线性发生率、饱和治愈函数及Logistic函数构造的SEIR模型对微信谣言传播过程进行分析与研究，掌握其传播机理，为今后微信社交网络的健康发展提供理论依据.

1 具有双线性发生率和饱和治愈率的微信谣言传播模型

在传统的SEIR传染病模型中，将t时刻系统中的用户分为4种状态，分别是易感态（S）、潜伏态（E）、感染态（I）和免疫态（R）.类似地，研究微信谣言传播时，系统中的用户也可分为4种状态：S态，无知者，指在系统中对谣言不知情的用户；E态，潜伏态，指在系统中接收到谣言但未决定是否传播的用户；I态，传播态，指在系统中知道谣言并且传播的用户；R态，免疫态，指在系统中不信谣不传谣的用户.

在改良的SEIR模型中，部分免疫者会识别微信谣言的虚假性并通过转发等方式将真相注入微信平台，告知好友谣言的虚假性并形成广播效应.基于此将4类结点间的传播过程定义如下：

1）无知者（S）以Logistic曲线的增长率输入微信平台，无知者（S）以双线性发生率βSI接触谣言成为潜伏者（E），即知道谣言但还未决定是否传谣；

2）潜伏者（E）以ε的概率成为传播者（I），由于某种原因失去传播的兴趣得知真相以γ的概率成为免疫者（R），以μ的概率遗忘谣言；

3）传播者（I）以饱和接触率成为免疫者（R），以μ的概率遗忘谣言；

4）免疫者（R）以μ的概率遗忘谣言.

基于上述描述，节点状态转换即微信谣言传播规律用图1来描述，系统中的参数定义及其意义如表1所示.在以下讨论中，S(t),E(t),I(t),R(t)分别代表t时刻4类微信用户占全体微信用户的数量的比例，模型中我们假设S(t),E(t),I(t),R(t)均为关于t的连续可微函数.

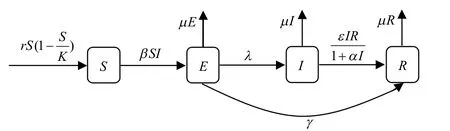
图1 无知者、潜伏者、传播者和免疫者的转换关系Fig 1 The Transformation Relationship between the Ignorant,the Lurker,the Disseminator and the Immune

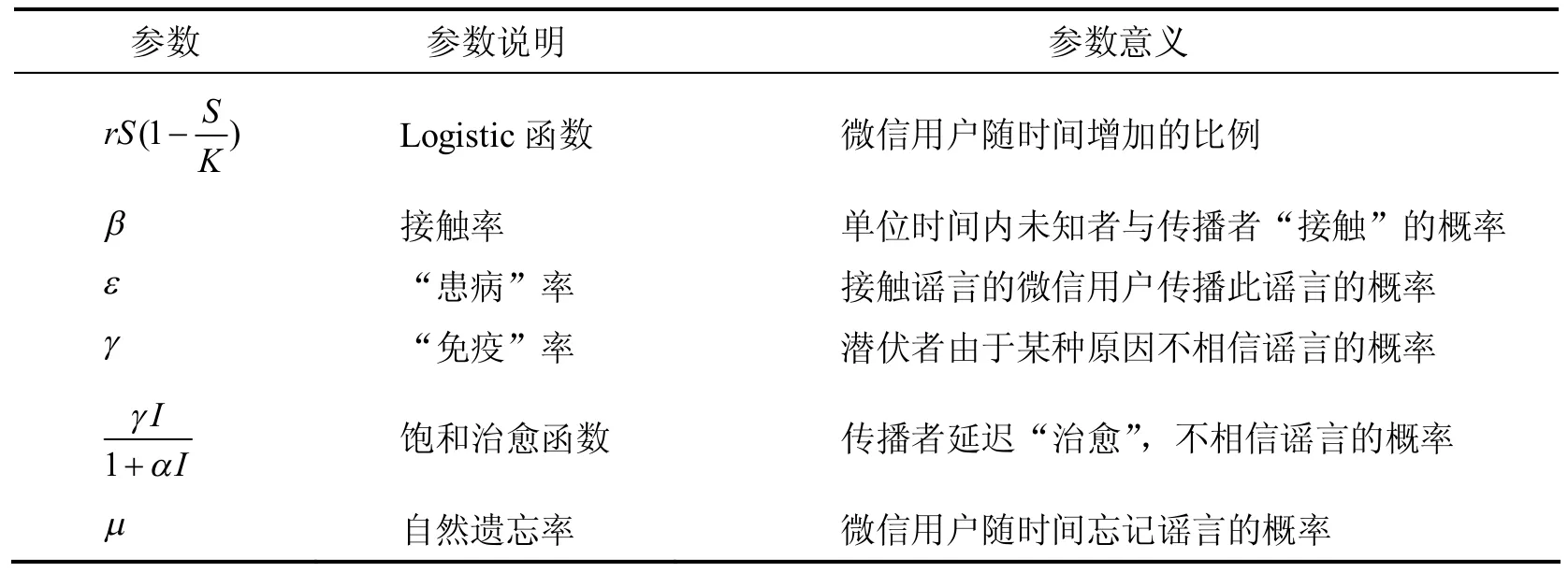
表1 参数定义及其意义Table 1 The Parameter Definition and Its Significance

根据系统动力学建模思想，可以建立如下的具有双线性发生率和饱和治愈函数的SEIR微信谣言传播模型：

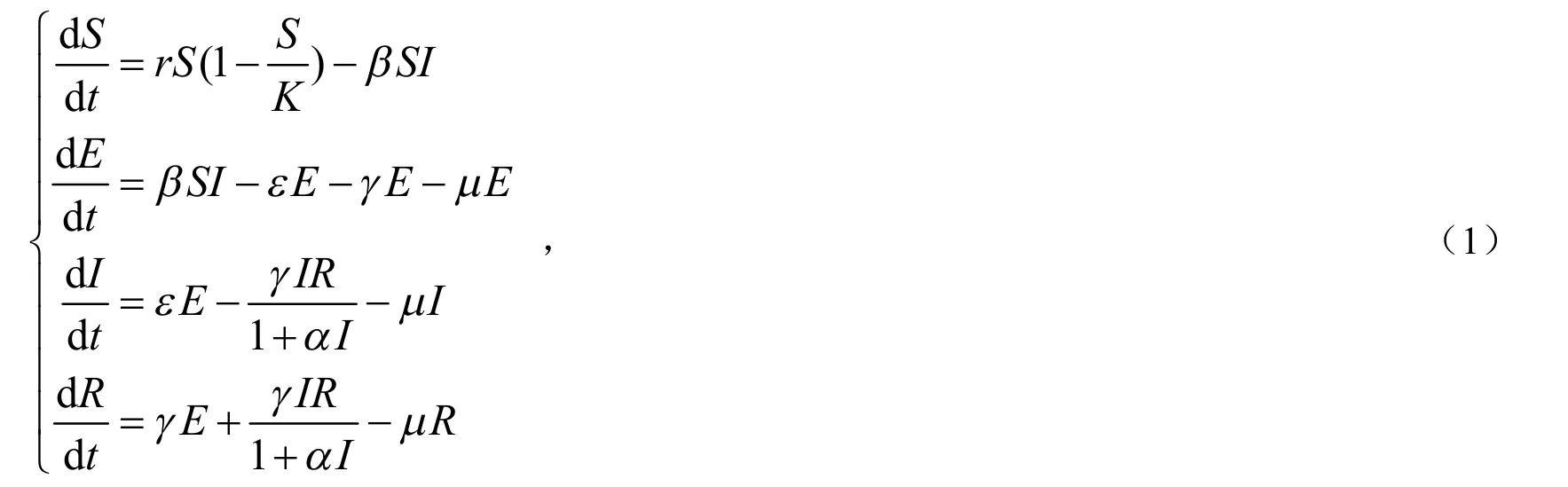
其中这些系数都是（0,1）之间的数.下面将研究模型的平衡点、传播阈值及平衡点的稳定性，从而揭示微信谣言的传播规律.

2 基本再生数与无谣言平衡点的稳定性

根据模型的实际背景，将在有界区域

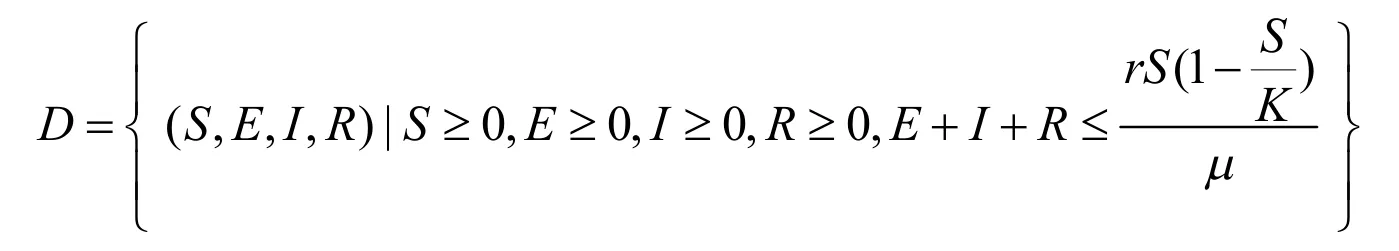
内考虑模型的平衡点.

据传染病模型的相关研究成果可知，传染病在传播过程中存在传播阈值R0（又称基本再生数）.当阈值R0≤1时，微信谣言会随着时间自然消亡；而当R0＞1时，微信谣言就会在一定范围内爆发.下面我们将寻求微信谣言的传播阈值R0.

定理1 模型（1）存在无谣言平衡点x0=(K,0,0,0)，模型的基本再生数

证明：当E=I=0时，x0易证.现证基本再生数R0.首先构造基本再生矩阵FV-1，其中

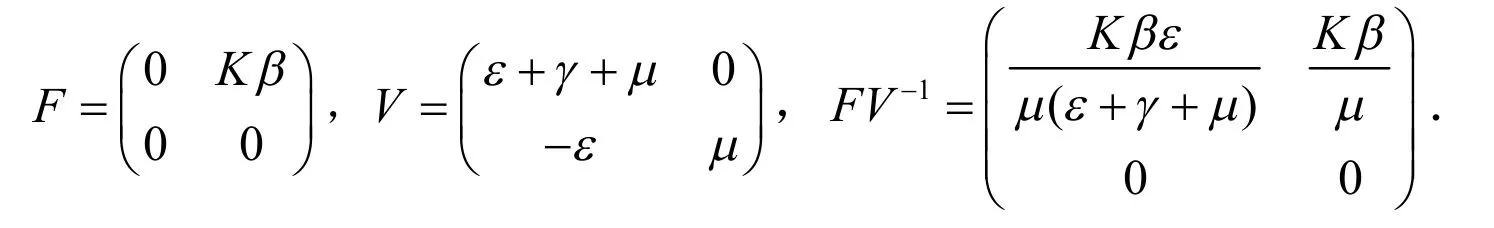
由基本再生数的计算方法可知FV-1的谱半径，即为基本再生数，故

定义1[10]考虑系统w=g(w)，g∈C[Rn,Rn]，g(wo)=0.令B是g(w)在平衡点w0处的Jacobian矩阵.若矩阵B的所有特征值都小于零，则系统在平衡点w0处局部渐近稳定；若矩阵B的所有特征值都大于零，则平衡点w0不稳定.

定理2 当R0≤1时，无谣言平衡点x0是局部渐近稳定的；而当R0＞1时，x0不稳定.

证明：模型（1）在x0处的Jacobian矩阵其特征方程|λE-J(x0)|=0.显然λ1=-r，λ2=-μ.其余两特征根由以下方程决定：

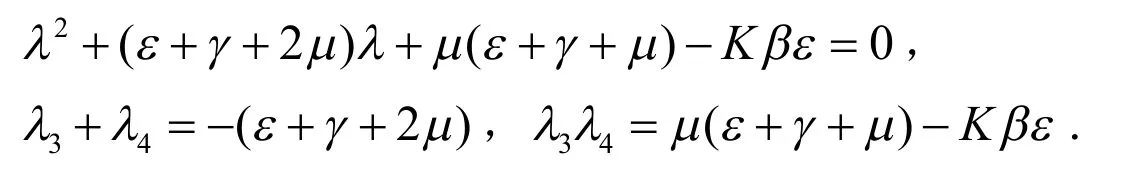
当R0＜1时，有Kβε＜μ(ε+γ+μ)，此时λ3λ4＞0，故λ3＜0，λ4＜0.

综上，模型（1）在无谣言平衡点x0处是局部渐近稳定的.由定理1与定理2可知，就是模型（1）的传播阈值.命题得证.

3 地方性谣言平衡点的存在性与稳定性

以上求出的无谣言平衡点是一种理想的状态，真实的微信信息传播过程中是不存在的.为了描述真实的微信谣言传播过程，我们在有界区域D内讨论地方性谣言平衡点.

首先讨论地方性谣言平衡点的存在性，有如下结论成立：

证明：令模型（1）的左端为零，可以得到：

其中d=ε+γ+μ.将（2）代入模型（1）的第三个方程得：

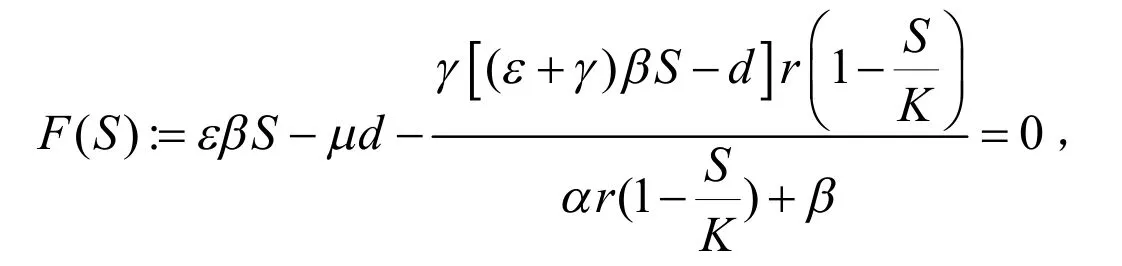
函数F(S)单调增加，注意到因此当且仅当时，方程F(S)=0有唯一根S*∈(0,K).进而由（2）可以得到：

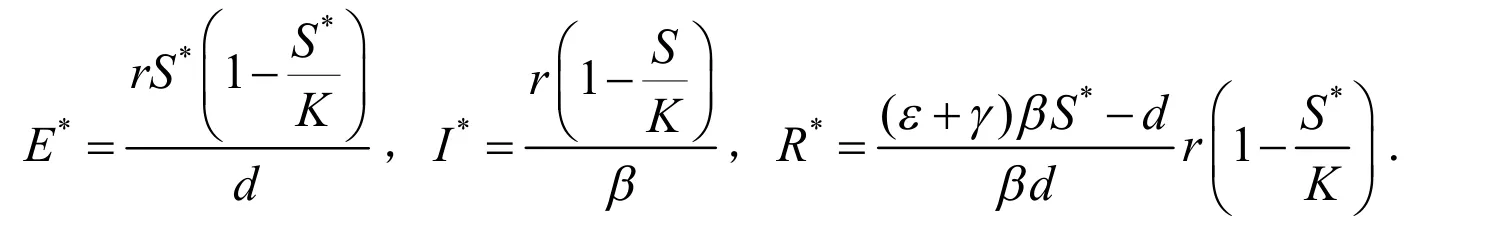
因而，关于地方性谣言平衡点（正平衡点）x*=(S*,E*,I*,R*)有以下定理.

证明：模型（1）在x*处的Jacobian矩阵为：

由Routh-Hurwitz判据可知J(x*)的所有特征根都具有负实部，则模型（1）在地方性谣言平衡点x*处是局部渐近稳定的[11].命题得证.

4 结 论

本文研究了用户数量增长符合Logistic曲线、具有双线性发生率和饱和治愈率的SEIR微信谣言传播模型，利用基本再生数定义得到利用Routh-Hurwitz判据得出结论：当R0＜1时，无谣言平衡点x0在D内局部渐近稳定，微信谣言会随着时间自然消亡；当R0＞1时，存在地方性谣言平衡点x*且局部渐进稳定，即若不对谣言加以管控，谣言将持续存在并传播下去.对于模型的全局动力学特性，还需继续研究（如对模型进行数值仿真），希望本文对其他学者就微信谣言方面的研究有所帮助.