基于自适应逐步混合检测多元Birnbaum-Saunders分布的相依竞争风险模型统计推断

杨 超

(温州大学数理与电子信息工程学院，浙江温州 325035)

在加速寿命试验中，通过可靠性分析考虑被测单元、产品和系统的各种失效原因的方法称为竞争风险模型[1].Wu等[2]通过使用I型渐进混合截尾方法，在竞争风险的寿命服从威布尔分布时，通过恒定应力加速寿命试验得到最大似然估计和贝叶斯估计[2].Mao等[3]给出了具有指数竞争失效模型的广义I型混合截尾数据的精确似然推理.基于未知参数的极大似然估计，利用条件矩母函数建立参数的精确条件分布，讨论了参数的矩性质和精确约束区间[3].Balakrishnan等[4]将竞争风险模型引入加速寿命试验环境下的单次器件测试分析中，并开发了EM算法来计算模型参数的估计量.Zhang等[5]分析了渐进式I型混合审查下具有竞争风险的部分加速寿命试验中的竞争风险模型，基于被篡改的失效率模型，得到了Weibull未知参数和加速度因子的最大似然估计、贝叶斯估计、渐近CI和最高后验密度可信区间.

但是，竞争风险的独立性假设在可靠性分析中具有较大的局限性.作为基本模型，二元竞争风险模型被广泛用于讨论多元竞争风险.在m（＞2）个元件的寿命测试中，m个元件竞争失效的原因可分为两个部分.一个是导致故障时间的失效原因，另一个原因是其他m-1个元件竞争失效.因此，考虑多元竞争风险之间的相关性对于统计推断是非常重要和必要的.

1 模型设定

1.1 多元Birnbaum-Saunders分布

若T的累积分布函数可以显示如（1）式，那么随机变量T就具有两个参数的Birnbaum-Saunders分布（Birnbaum-Saunders分布以下简称BS分布，多元Birnbaum-Saunders分布以下简称MBS分布）：

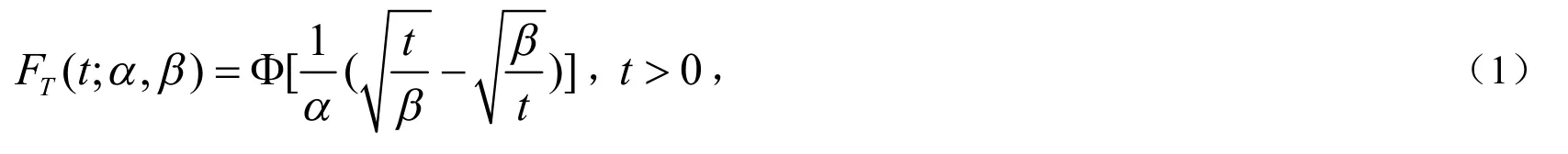
其中Φ(·)是标准正态累积分布函数，α＞0和β＞0是形状参数和尺度参数.也就是说，T～BS(α,β).

T的相应概率密度函数可以由（2）式给出：

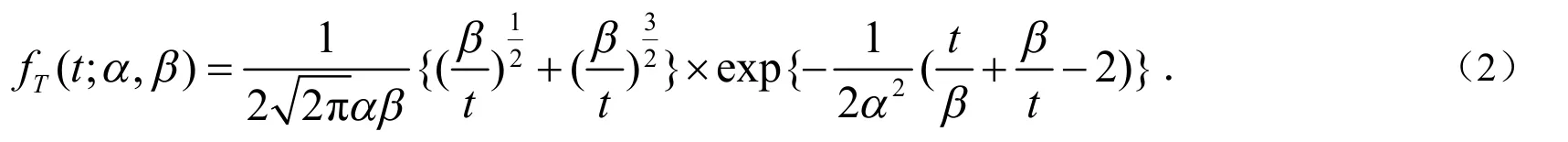
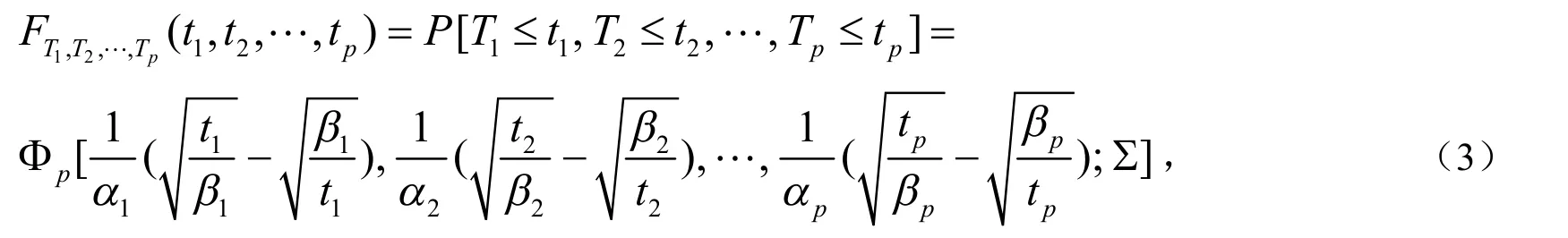
其中参数α1＞0,α2＞0,…,αp＞0，β1＞0,β2＞0,…,βp＞0，Σ是p×p正定扩散矩阵对于t1＞0,t2＞0,…,tp＞0.Φp(u,v;Σ)是一个标准的多元正常随机向量(u,v)的累积分布函数与正定扩散矩阵Σ.

T1,T2,…,Tp的联合概率密度函数由（4）式给出：

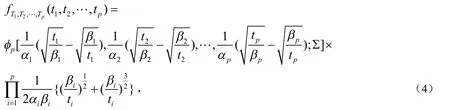
联合概率分布函数可以表示为

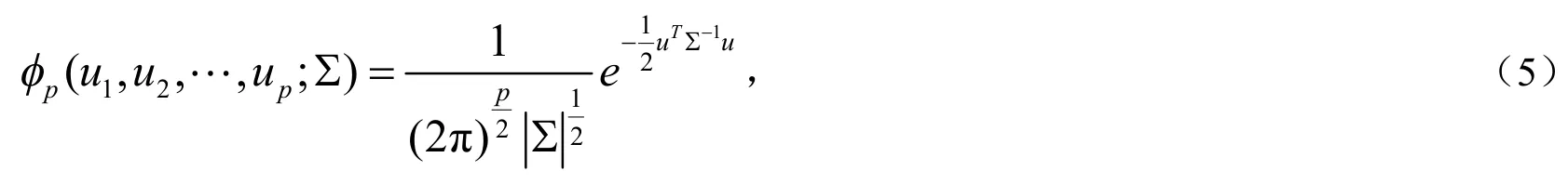
其中u=(u1,u2,…,up)T.

下面的定理中可以提供多元MBS分布的边际分布和条件分布.

定理1 若T～MBSp(α,β,Σ)，让T,α,β,Σ按如下方式划分

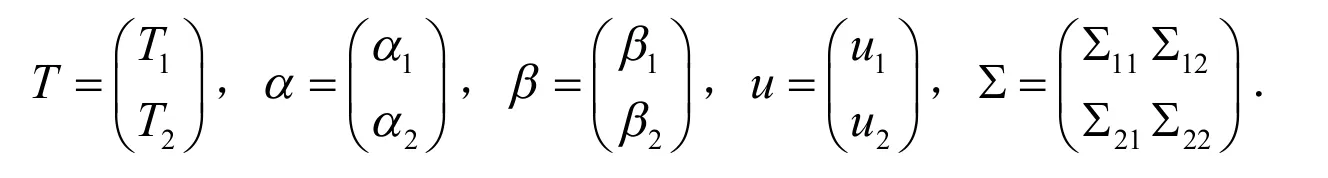
其中T1,α1,β1全是q×1维向量，Σ11是一个q×q维的矩阵，其余的元素与之相应匹配，可得出：

1）T1～MBSq(α1,β1,Σ11)以及T2～MBSp-q(α2,β2,Σ22)；

2）当T2=t2，T1的条件累积分布函数是

3）当T2=t2，T1的条件概率密度函数是

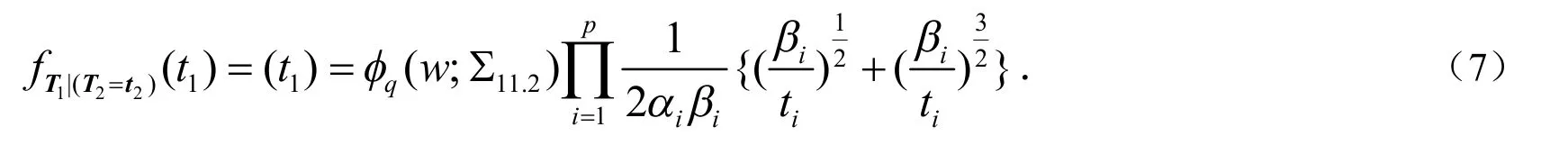
证明：

对于1）的证明，可通过令（3）式中tq+1→∞,…,tp→∞简单得出.

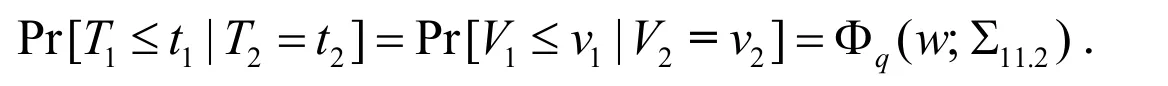
1.2 相依竞争风险模型

考虑p个相依竞争风险因素T1,T2,…,Tp和边际BS分布，也就是(T1,T2,…,Tp)～MBS(α,β;Σ)，且Tj～BS(αj,βj)，j=1,2.T1,T2,…,Tp之间的相依结构是由多变量随机向量的MBS分布(T1,T2,…,Tp)描述的，联合生存函数和累积分布函数(T1,T2,…,Tp)可以分别表示为：

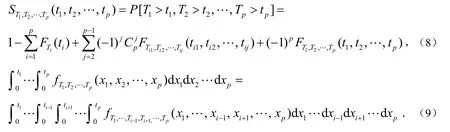
令T=min(T1,T2,…,Tp)作为一个系统的寿命，对于j=1,2,…,p的次密度函数fj(t)可以被计算为：

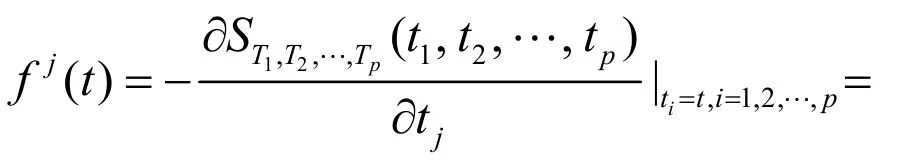
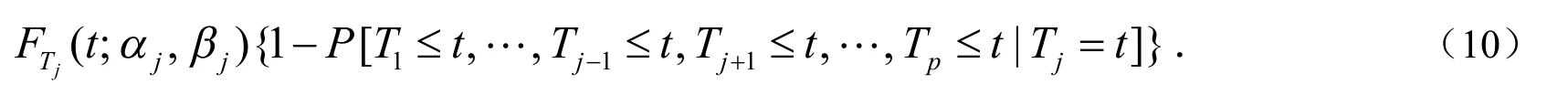
T的生存函数是S(t)=ST1,T2,…,Tp(t,t,…,t)，在相依竞争的风险模型中，潜在的失效时间T=min(T1,T2,…,Tp)和在一组{1,2,…,p}中有一个整数值的失效索引C，它们形成相依竞争的风险数据(T,C).

1.3 基于自适应逐步混合检测方法的加速寿命试验的数据描述

在k级恒定应力加速寿命试验中，有k个应力水平s1＜s2＜…＜sk和正常应力水平s0.在每个应力水平si，p依赖失效因子(Ti1,Ti2,…,Tip)，服从MBS(αi1,βi1,αi2,βi2,…,αip,βip;Σ)分布，其中i=1,2,…,k.将n个测试单元置于加速寿命试验中，并用ni个测试单元将它们分组成k组.在si处对ni个测试单元进行测试，并指定预定时间τi、预期ri故障并在故障时间Ril(l=1,2,…,ri)移除单元.

给定恒应力加速寿命试验中的预定时间τi，可以在具有相应终止时间min{Ti,ri:ri:ni,τi}和max{Ti,ri:ri:ni,τi}的type-I型渐进混合检测方法和type-II型PHCS中观察到应力水平si处的故障时间，其中Ti,ri:ri:ni是应力水平si下的第ri个故障时间.在type-I型PHCS中，当测试单元具有长寿命时，可能发生零失效时间.在type-II型PHC中，实验可以在足够长的时间之后结束.这些缺点会影响统计推断的效率.Gasbarra等[6]提出了自适应渐进混合检测方法，通过重新确定Ril值，自适应PHCS提供了克服PHCS缺陷的有效方法.

如果第ri个逐渐删失的失效时间发生在时间τi之前，则si下的实验在故障时间Ti,ri:ri:ni终止.也就是说则加速测试继续，为了尽快到达第ri个逐渐审查的故障时间，在时间τi之后，设定

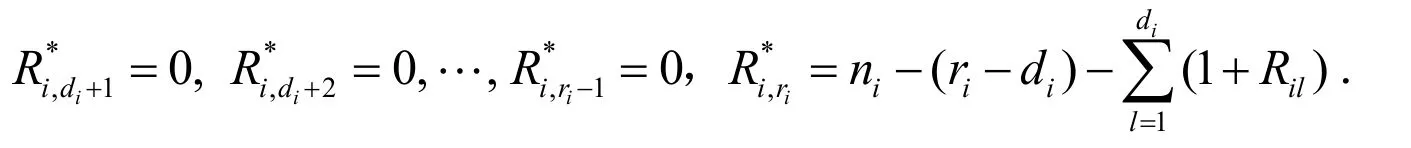
如Gasbarra等[6]中提出的这种设定使我们在时间iτ之后尽快结束实验，此时直到在应力水平si处观察到ri次失效，然后给出加速竞争风险数据.对于如果失败指数cil=1，其中δil=1；否则δil=0.

1）应力水平仅改变BS分布的尺度参数，因此α1j=α2j=…=αkj=αj,j=1,2,…,p.

2）尺度参数与应力水平之间的关系一般是对数线性的，即

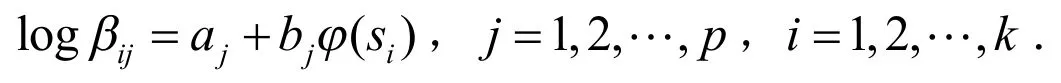
基于上述假设和数据描述，得到未知参数θ=(α1,α2,…,αp,βi1,βi2,…,βip;Σ)，i=1,2,…,k，其中αj＞0，Σ＞0，β1j＞β2j＞…＞βkj＞0当j=1,2…,p.

2 极大似然估计

在上述加速竞争风险模型的假设下，似然函数被表示为

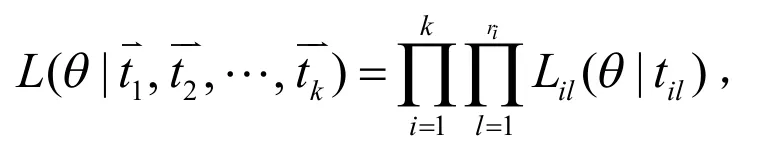
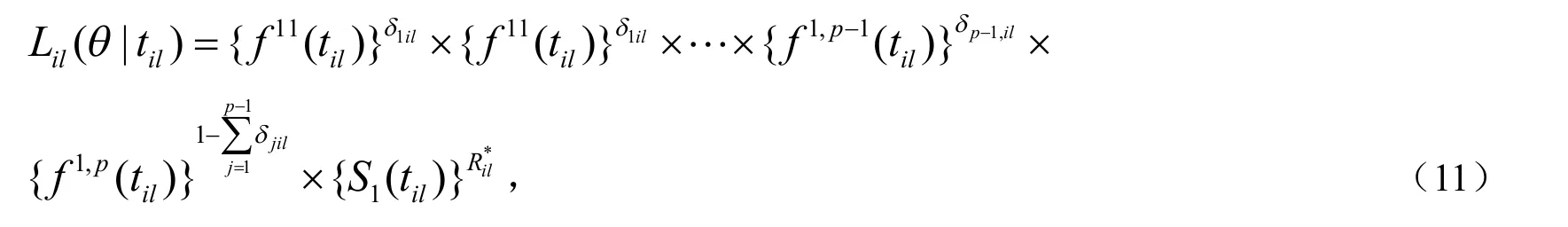
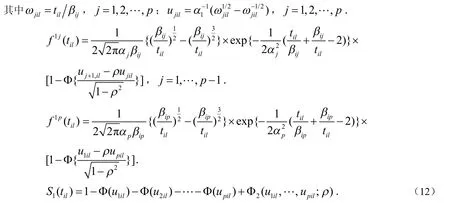
对于j=1,2,…,p在故障时间内，在应力水平S1下，f1j(til)是次密度函数，S1(til)是生存函数.Lil(θ|til)的对数似然函数表示为（13）式，因此有关于单个参数的似然方程

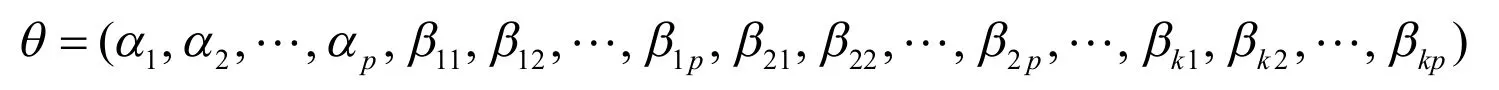
由（14）给出.

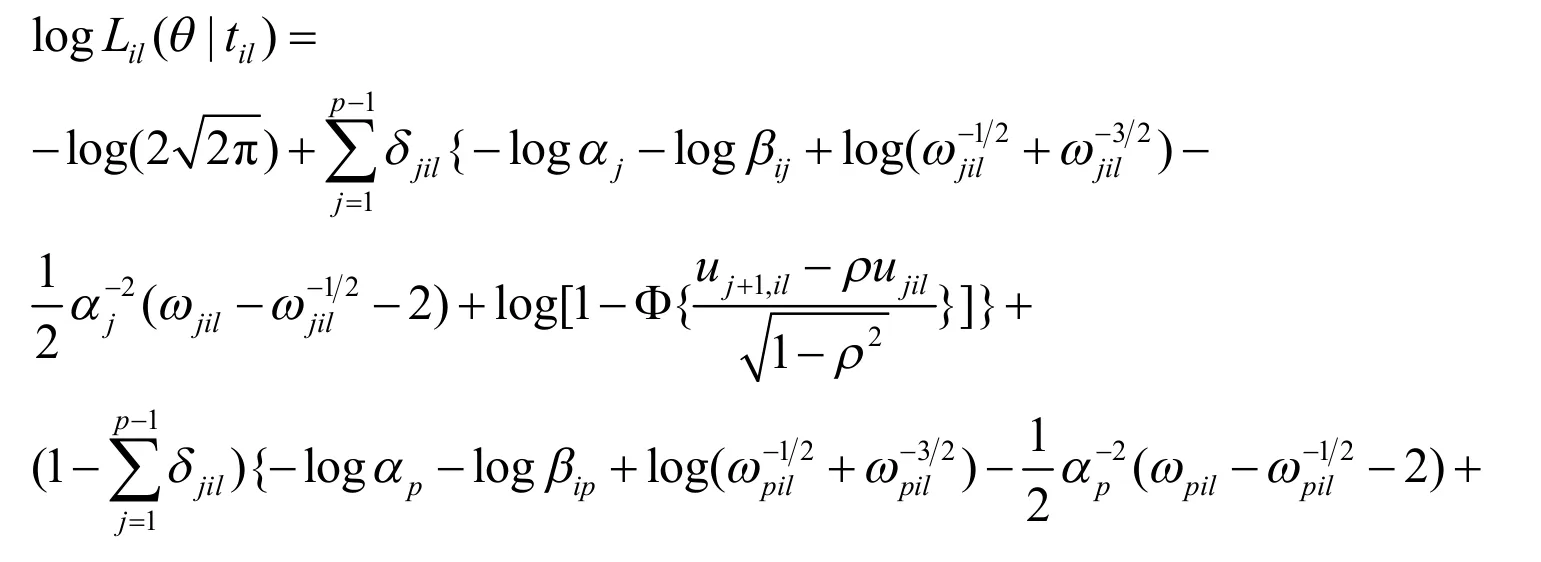
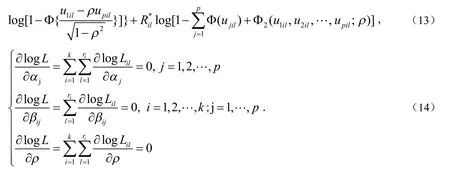
由于（14）式中方程的复杂形式可能在显式表达式中不能得到未知参数的显式极大似然估计量，可通过数值迭代算法，如Newton-Raphson算法得到极大似然估计的数值结果.

3 统计推断

3.1 初始值设定

在竞争风险模型中，失败的原因来自于不同参数的MBS分布.基于这种相依结构，竞争风险之间的独立性以及多个竞争风险的形状和规模参数的关系可能是值得关注的.讨论了下列假设的似然比检验：

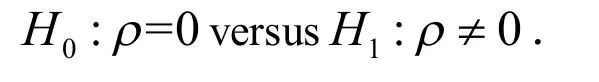
在试验中，H0情况下通过求解似然方程得到参数的极大似然估计：

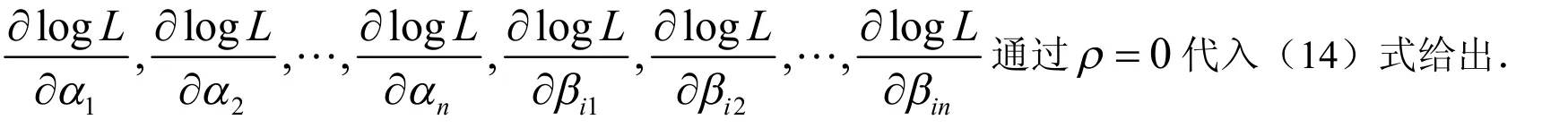
3.2 极大似然估计

实际应用中，在寿命试验中需要对试验者、制造商和客户提供单位或产品的界限.具有相关竞争风险，在故障时间til（l=1,2,…,ri，i=1,2,…,k）有幸存的单元被移除，因此测试单元的故障时间是未观测到的.在该条件下，用某个测试单位表示某个元件的第s个统计数据.

已知极大似然估计量

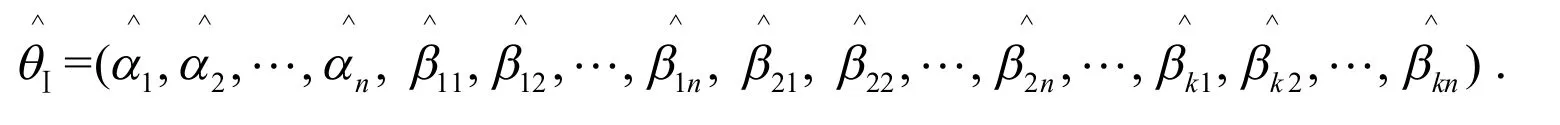
si下的的条件密度函数可表示为：

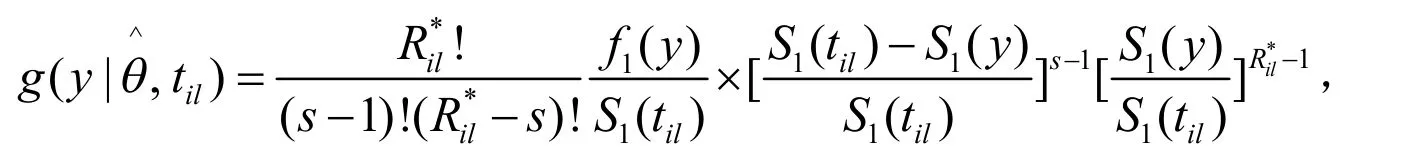
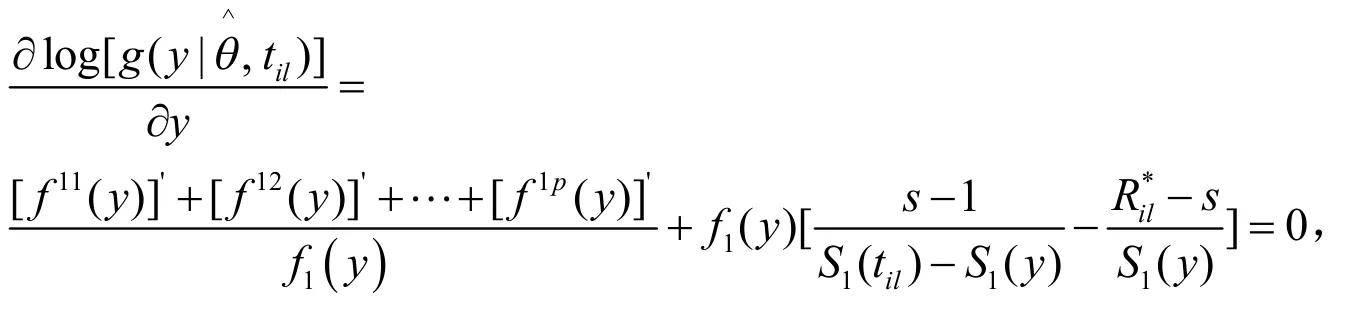
其中

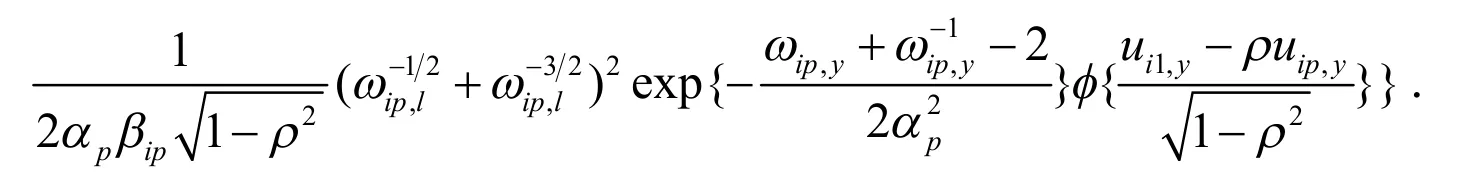
4 结论与讨论

考虑了多元MBS分布在三个部件系统的情形，设定初始值：

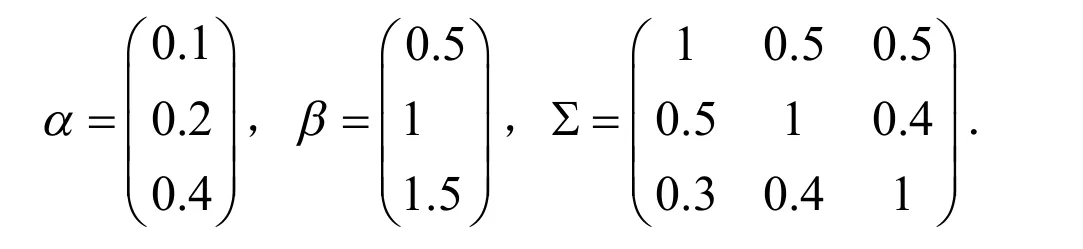
在常应力下，我们从MBS分布中分析具有相依竞争风险的自适应渐进混合截尾数据，在三个部件的情形下通过设定抽取样本数为5 000，得到相应的极大似然估计和矩估计.在兴趣假设的基础上，讨论了似然比检验.进行了仿真研究，得到了估计量和预测值的数值结果，见表1.

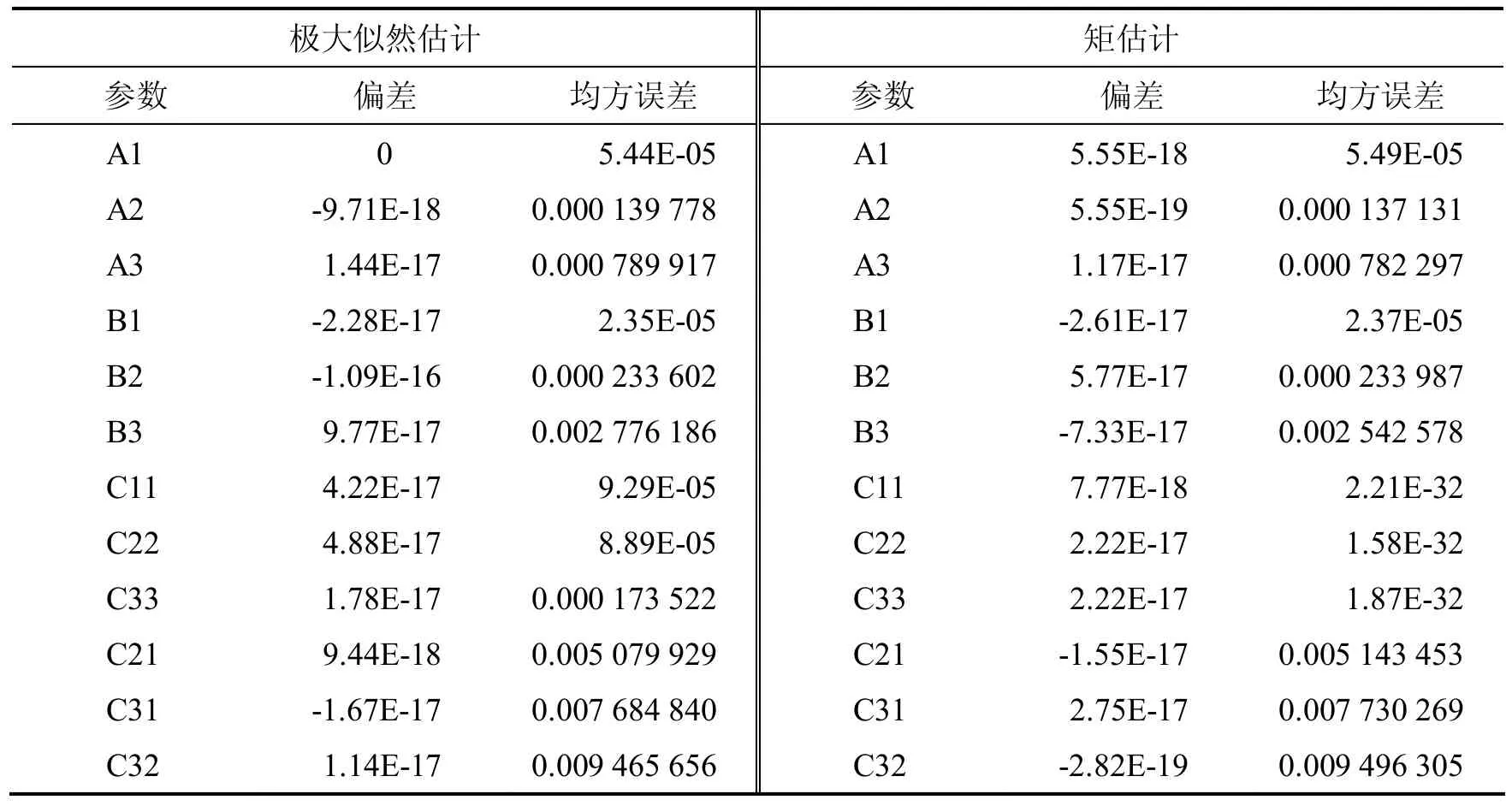
表1 极大似然估计和矩估计Fig 1 Maximum Likelihood Estimation (MLE) and Moment Estimation (ME)

我们比较了极大似然估计和矩估计下各个参数的偏差与均方误差，二者模拟结果比较接近，偏差与均方误差数值均比较小，模拟效果较好.仿真研究表明，所提出的模型和方法可用于基于竞争风险数据的统计推断.在以后的工作中，可以进一步研究加速寿命试验下自适应渐进混合截尾数据下基于相关竞争风险模型的贝叶斯推理.