基于加罚方法的向列型液晶流问题的一阶时间半离散格式

龚 欢

(温州大学数理与电子信息工程学院，浙江温州 325035)

在本文中，考虑以下的流体动力学模型：

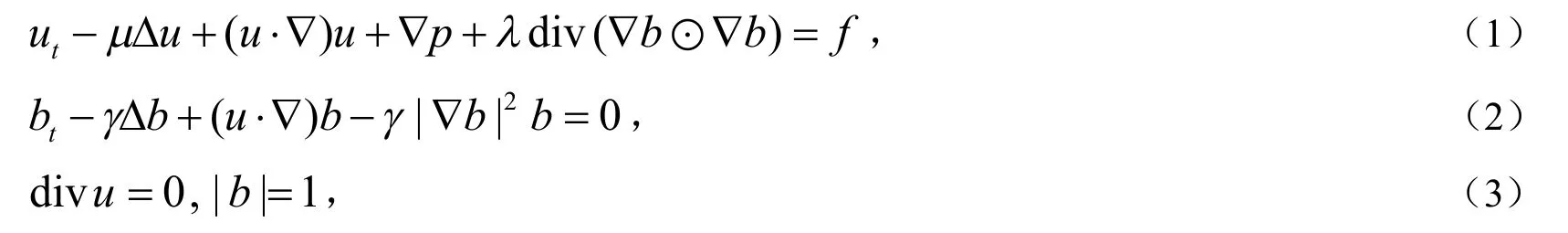
其中，t∈(0,T]，Ω⊂R2是一个有界凸区域，且边界光滑.u(x,t):Ω×[0,T]→ℝ2和p(x,t):Ω×[0,T]→ℝ分别代表速度和压力.b(x,t):Ω×[0,T]→S，其中S是ℝ2中的单位圆，代表着宏观分子取向.f:Ω×[0,T]→ℝ2为外力.常数μ,λ,γ为三个正常数分别表示着粘性系数、弹性系数和弛豫时间系数.∇b⊙∇b为2×2矩阵.如果b是一个常映射，则上述系统简化为不可压缩Navier-Stokes方程[1]，如果u=0，则上述系统简化为热调和映照[2].

为了研究方程（1）-（3），赋予如下的初始条件和边界条件：

其中n表示在∂Ω中单位外法向量，这里要求初始向量函数u0和b0满足条件divu0=0和|b0|=1.

方程（1）-（3）首先是由林芳华教授在文献[3]中作为Ericksen-Leslie模型的简化模型导出的，用于描述由Ericksen[4-5]和Leslie[6]所提出的向列型液晶流动模型，它是在流动速度u和类似于旋转液晶流的微观取向b的影响下对材料时间演化的宏观连续描述.但研究系统（1）-（5）的困难之一是非线性约束|b|=1，通常的方法是采用Ginzburg-Landau加罚函数去代替（2）式中的2|∇b|b，而不考虑非线性约束|b|=1.此时考虑如下的加罚问题：

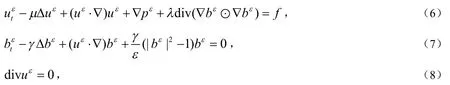
其中ε＞0为加罚参数.（6）-（8）式首先是由Lin和Liu在文[7]中引入的，文[7]证明了三维问题全局弱解和局部强解的存在性.然而由于解的估计很大程度上取决于ε，所以在（6）-（8）式中当ε趋于0时，加罚问题方程（6）-（8）的解是否趋于原问题方程（1）-（3）的解仍不清楚.

近几年许多学者对向列液晶流动问题的数值方法也进行了研究，Liu和Walkington在文献[8]中对加罚问题方程（6）-（8）的数值方法首先进行了研究，并采用3ℚHermite有限元来逼近bε.为了避免使用Hermite有限元，随后Liu和Walkington又在文[9]中研究了混合有限元方法，并构造了全隐格式，虽然该格式是无条件稳定的，但每个时间步必须求解非线性问题而需消耗大量的数值求解时间，正如文[10]中所指出的，在文[8-9]中导出的误差估计依赖于ε，这将导致非常小的时间步长为避免时间步长的强约束条件，Becker等在文[10]中通过引入研究了一种新的混合有限元方法，所提出的完全离散格式仅在求解wε时是非线性的，并且满足离散的能量不等式.在文[10]中，Becker等证明了当h,τ→0时数值解的适定性和收敛性，并没有给出误差估计.最近An和Su在文[11]中研究了求解（1）-（5）式的线性化半隐全离散有限元算法，在构造该算法时没有考虑非线性约束条件|b|=1，并证明了该全离散有限元算法具有最优阶的有限元时空误差估计.

本文将基于一种新的加罚方法，在不考虑非线性约束条件|b|=1的情况下，构造新的一阶线性化时间半离散格式.在时间步长和加罚参数满足τ=ο(ε)的条件下，我们证明了所构造的半离散算法具有一阶时间收敛精度.

1 预备知识

本文采用标准的Sobolev空间记号[12].用(.,.)表示L2(Ω)的内积，采用C,C0,C1,C2…表示正常数，它们可依赖于u,p,b,f,μ,λ,γ，但不依赖于加罚参数ε＞0和时间步长τ.

引入空间：

定义双线性形式：

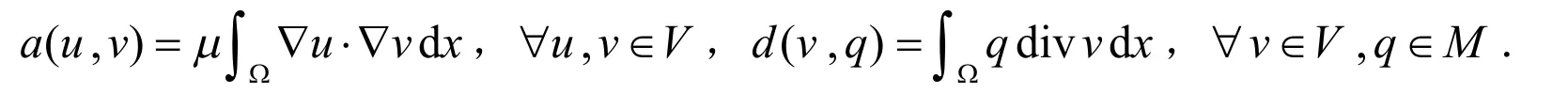
定义三线性形式：

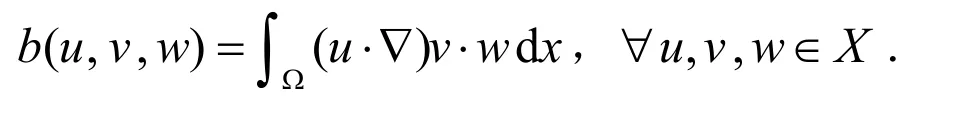
通过积分可得到：

记正交投影算子PH:L2(Ω)→H，那么Stokes算子A定义为[1]：

关于问题（1）-（5）的适定性，首先引入如下定理.

定理1 若u0∈D(A)，b0∈H3(Ω)2和|b0|=1在Ω内几乎处处成立，对于给定的f∈L∞(0,T;H)∩L2(0,T;L4(Ω)2)，则存在T*＜T使得（1）-（5）式存在唯一的局部强解(u,p,b)并满足[13]：

记0=t0＜t1＜…tN=T是时间间隔[0,T]的一个均匀化分割，时间步长，τ=T/N和tn=nτ.记un=u(x,tn)，pn=p(x,tn)，bn=b(x,tn)，fn=f(x,tn).对序列记取初始值B0=b0，U0=u0，构造如下的线性化加罚迭代格式：

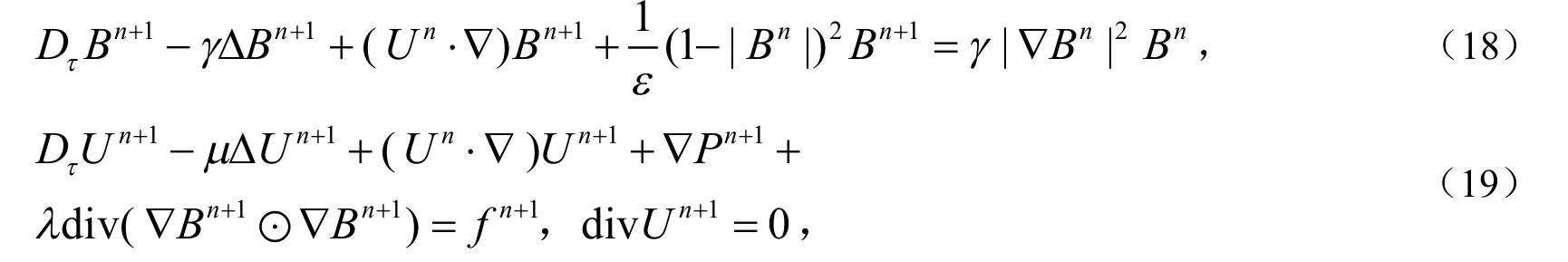
为了研究上述迭代格式的时间收敛阶，本文将应用如下的不等式：

2 主要结论

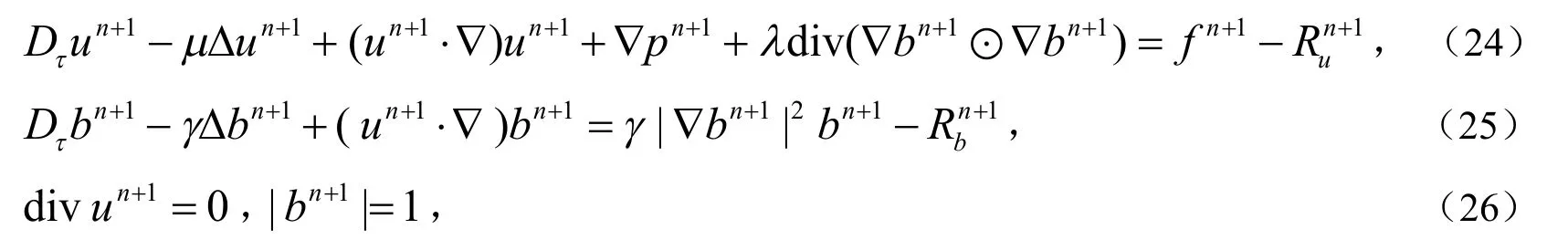
从（25）式中减去（18）式，并从（24）式、（26）式中减去（19）式得误差方程为：

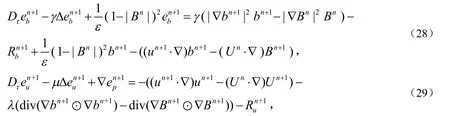
本文的主要结论如下.

定理2 在定理1的正则性条件下，对足够小的ε＞0，若时间步长τ满足τ=ο(ε)，则有：

证明：因为u0=U0=u0和b0=B0=b0，因此（30）式和（31）式对m=0成立.假设（30）式和（31）式对m≤n成立，根据数学归纳法，那么只需要证明（30）式和（31）式对m≤n+1也成立.（28）式乘以然后在Ω上积分可得到：

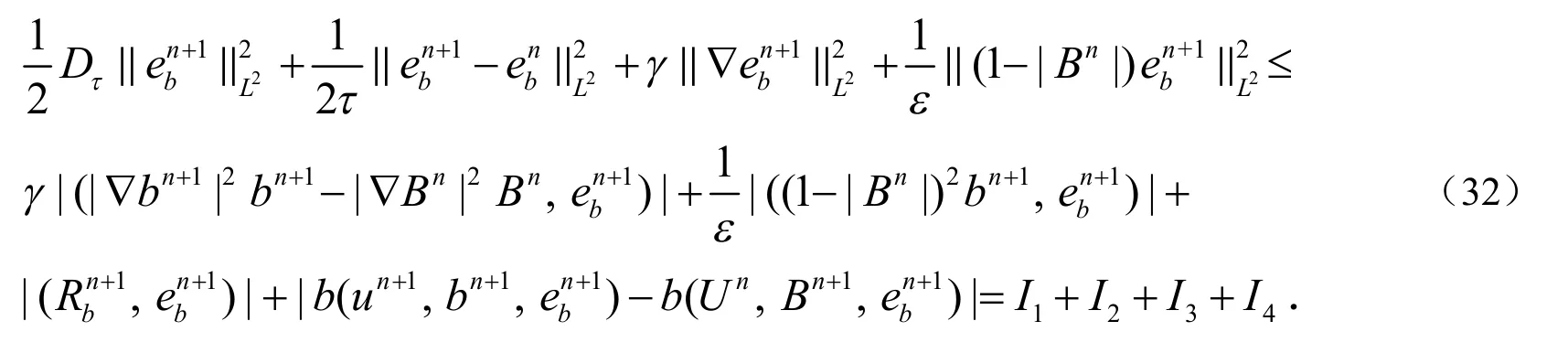
现在开始估计上式右端.根据

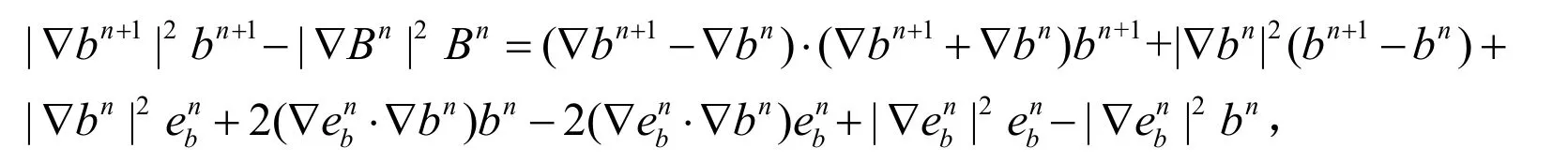
并使用（15）式，（16）式，（22）式，（30）式（对m≤n成立），Holder’s不等式和Young’s不等式，可估计I1如下：

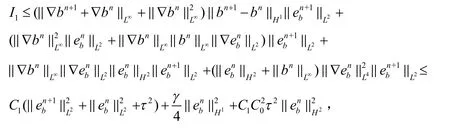
其中C1＞0与C0无关.这里使用

再由|bn|=1可得：

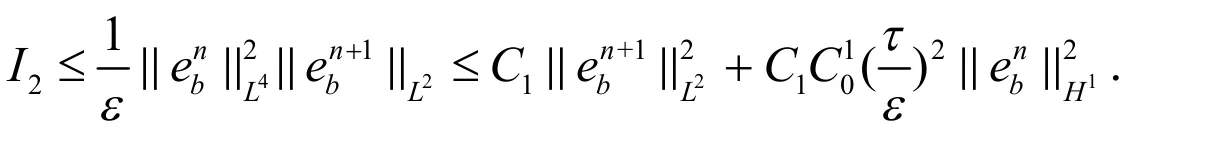
利用Holder’s不等式和Young’s不等式，可估计I3如下：

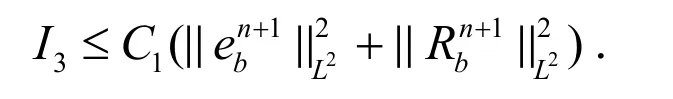
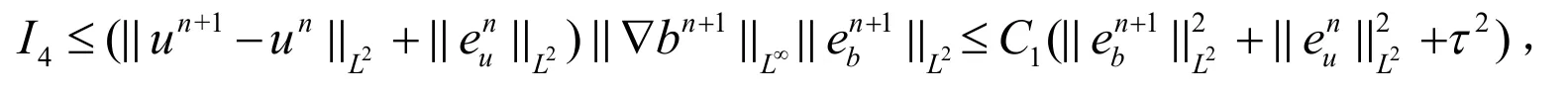
这里使用

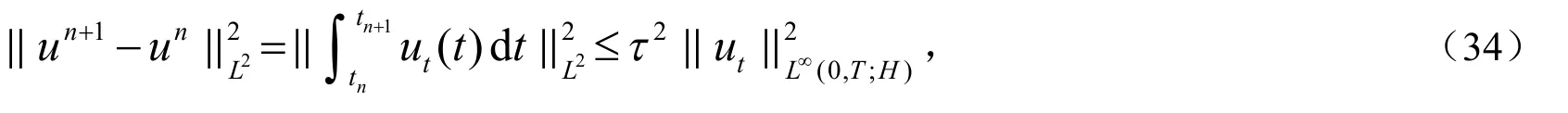
把I1,I2,I3和I4的估计带入（32）式得到：

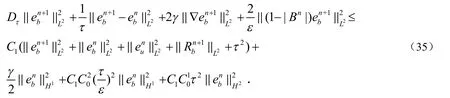
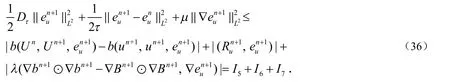
利用Holder’s不等式和Young’s不等式有：

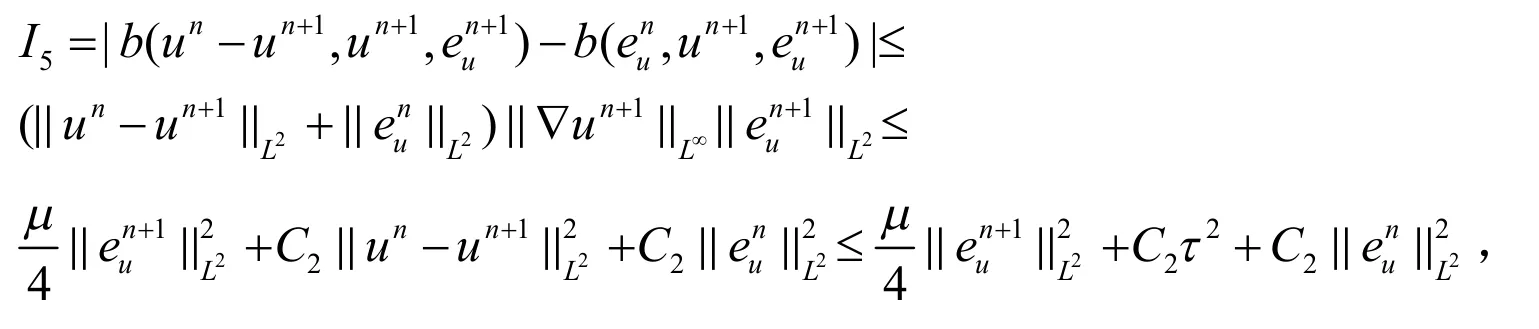
其中C2＞0与C0无关.

再根据

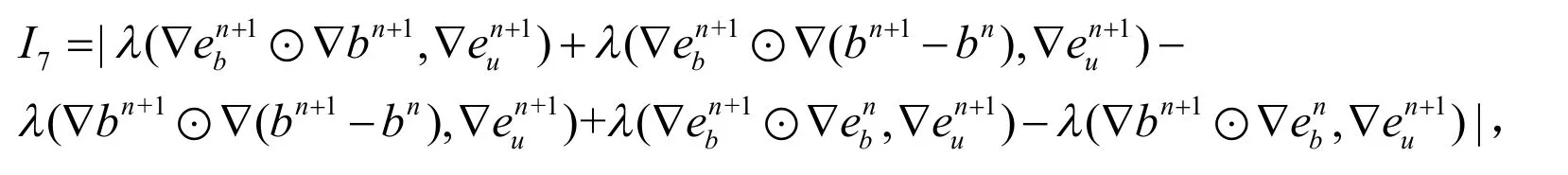
有：

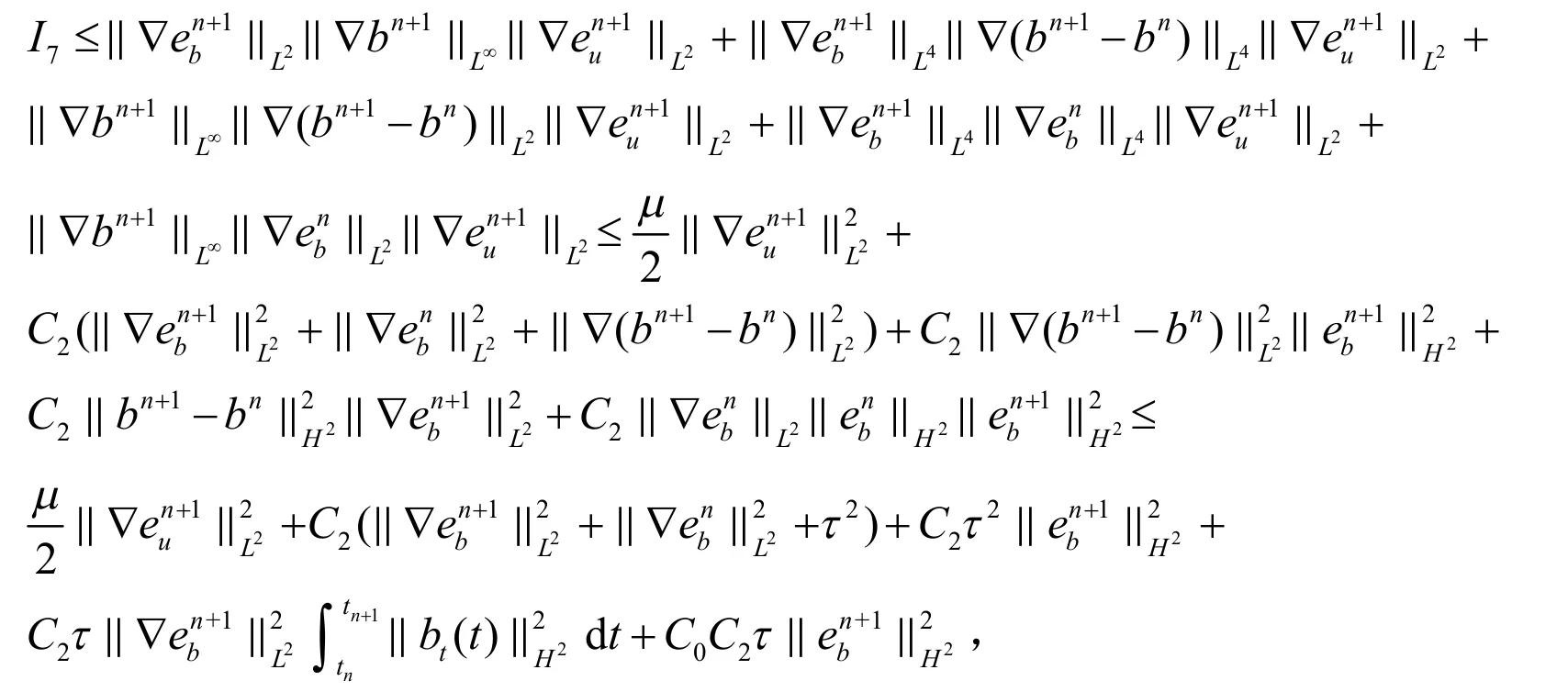
这里使用了（30）-（31）式（对m≤n成立）和

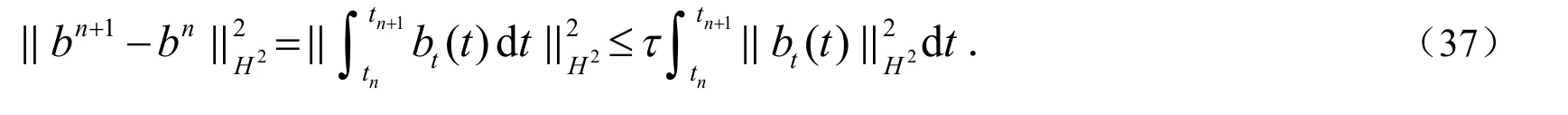
把I5,I6,I7带入（36）式中可得：

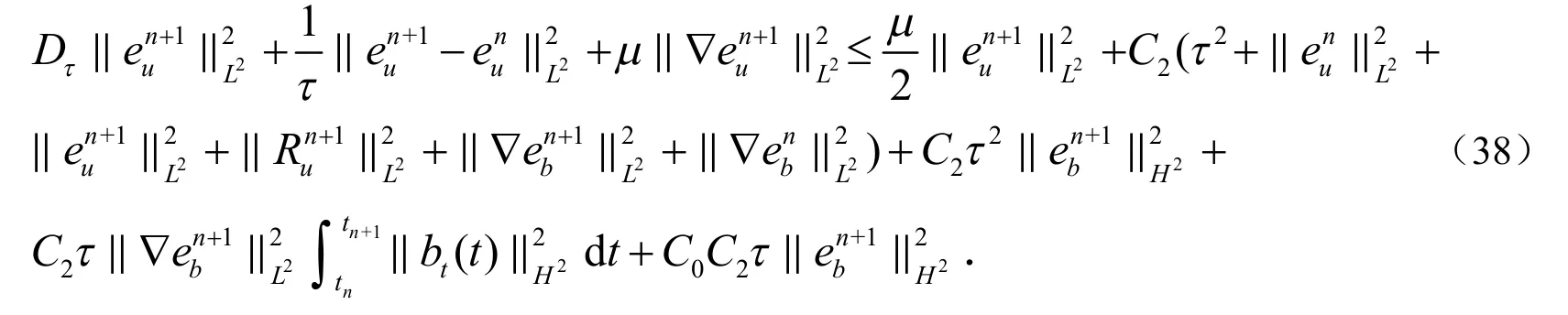
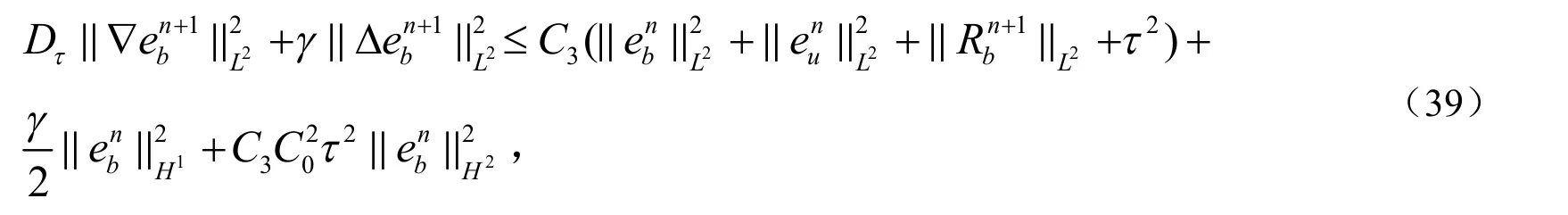
其中C3＞0与C0无关.

把（35）式，（38）式，（39）式加起来，得：

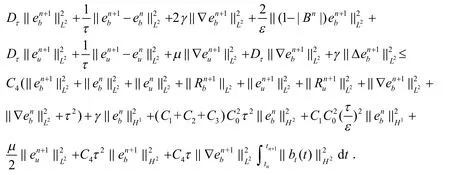
使用离散的Gronwall’s不等式[14]，并根据τ=ο(ε)，存在足够小的τ0＞0使得当τ＜τ0时有：

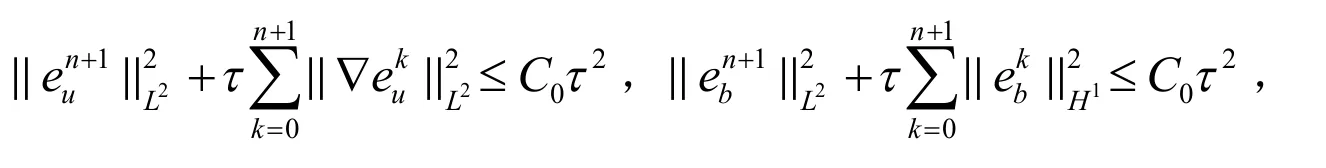
这样就证明了定理2的结论.