概率统计经典题突破

编者的话：“经典题突破方法”栏目里的例、习题选自名校模拟题或三年高考真题，推出本栏目的主要目的是让同学们更好地领悟数学解题思想方法，通过多解多变培养同学们多思多想的好习惯。学会解题反思，无疑是同学们学习的一条捷径，愿同学们不断地在反思中进步，在反思中收获！本期特约河南省项城市第一高级中学的张慧敏、韩维峥两位老师为同学们解读相关知识。愿同学们通过阅读，能从中感悟知识的结构与拓展，把握第19题、第20题的命题特点与趋势。

高中数学内容中的概率统计是大学统计学的基础，起着承上启下的作用。高考对概率统计内容的考查主要是古典概型、几何概型、统计的基础知识与方法。大题偏向于对统计知识、数据分析处理能力的考查。

一、经典题突破

例1 为了监控某种零件的一条生产线的生产过程，检验员每天从该生产线上随机抽取16个零件，并测量其尺寸（单位：cm）。根据长期生产经验，可以认为这条生产线正常状态下生产的零件的尺寸服从正态分布N（μ，σ2）。

（1）假设生产状态正常，记X表示一天内抽取的16个零件中其尺寸在（μ-3σ，μ+3σ）之外的零件数，求P（X≥1）及X的数学期望。

（2）-天内抽检的零件中.如果出现了尺寸在（μ- 3σ，μ+3σ）之外的零件，就认为这条生产线在这一天的生产过程可能出现了异常情况，需对当天的生产过程进行检查。

①试说明上述监控生产过程的方法的合理性。

②下面是检验员在一天内抽取的16个零件的尺寸：

9.95 10.1 9.96 9.96 10.0 9.92 9.98 10.010.2 9.91 10.13 10.0 9.22 10.0 10.0 9.95

2.考点定位与考查意图。

本题考查了统计学在生产实践中的应用，根据抽样统计，进行样本数据分析，反映了利用科学的方法搜集、整理、分析和提供关于社会经济现象、某些特定事物发展规律的数学思想，着重考查数据处理能力和运算求解能力，以及应用所学知识分析问题、解决问题的能力。考查正态分布、独立重复试验、对立事件、随机变量的概率与数学期望。概率统计重视实际应用是考查的重点，学生可以从解题过程中认识到统计与概率知识在生产与生活中所起的作用。通过对问题的解决，给学生展示了问题的提出、模型的建立、数据的整理与分析、统计与概率知识的应用，从而形成应用数学知识指导社会实践的意识，提高学生的综合实践能力。

3.错误原因。

概率统计中基本概念较多，理解不到位，文字阅读量偏大，数据的信息点多，计算量偏大，对于学生的运算能力要求较高，概率统计解答题的实际背景新颖，对阅读理解、推理分析、数据运算的要求较高，因此难度较大。

4.复习建议。

重视考纲考点的变化，高考全国卷中的概率统计解答题一直都比较重视数学应用，侧重于统计思想、数据分析与处理、结合生活实际的决策性问题，突出应用意识。

重视基本概念的梳理，概率与统计中的基本概念众多，在复习备考过程中引导学生回归教材，对教材中的基本概念进行梳理。

重视基本原理的研究，高考全国卷中的概率统计解答题重点考查统计与概率的基础知识、基本原理和基本方法，所以我们要加强对概率论与数理统计内容的学习与研究。

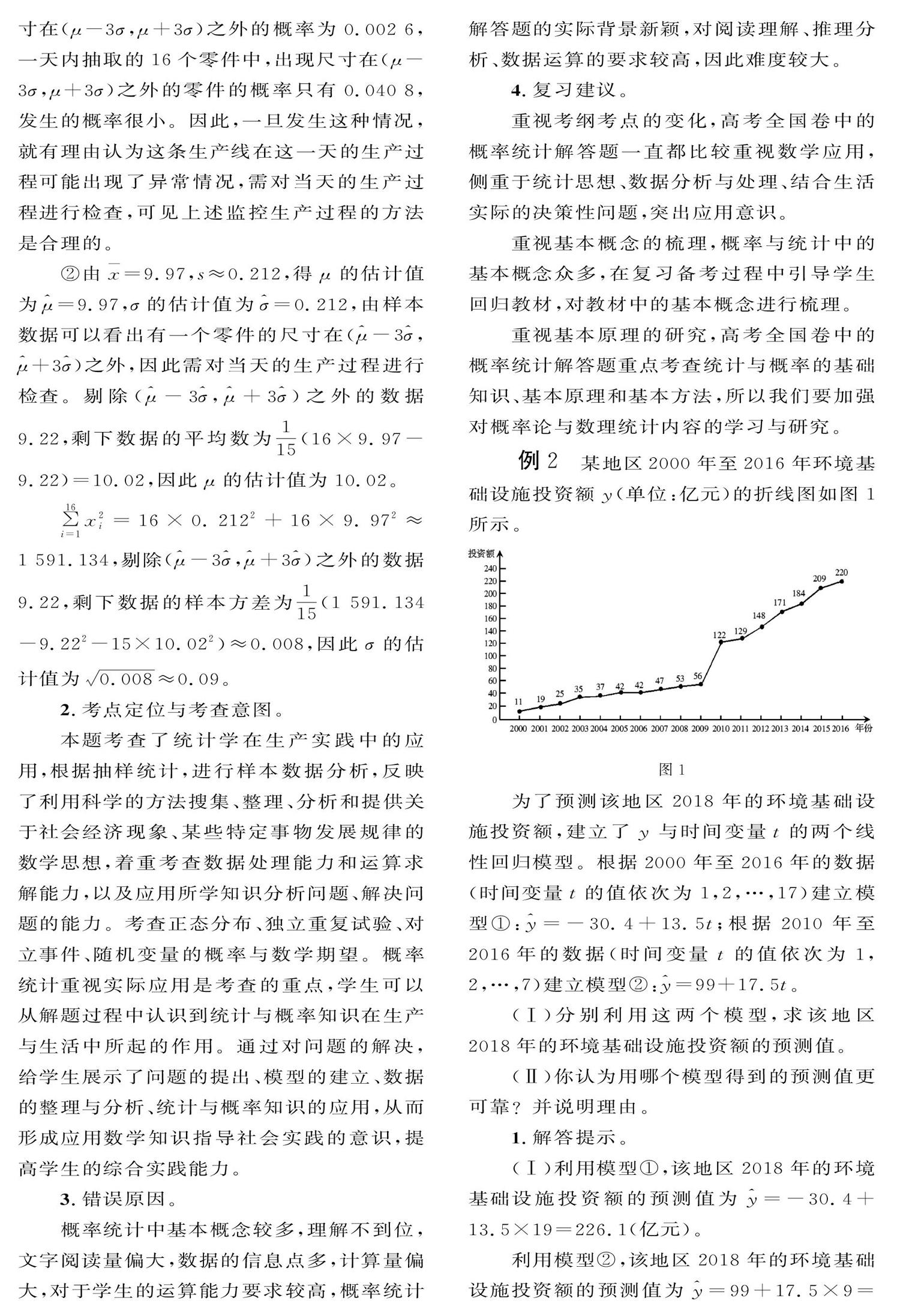
例2某地区2000年至2016年环境基础设施投资额y（单位：亿元）的折线图如图1所示。

为了预测该地区2018年的环境基础设施投资额，建立了y与时间变量t的两个线性回归模型。根据2000年至2016年的数据（时间变量t的值依次为1，2，…，17）建立模型①：y=-30.4+13. 5t;根据2010年至2016年的数据（时间变量t的值依次为1，2，…，7）建立模型②：y=99+17. 5t。

（I）分别利用这两个模型，求该地区2018年的环境基础设施投资额的预测值。

（Ⅱ）你认为用哪个模型得到的预测值更可靠？并说明理由。

1.解答提示。

（工）利用模型①，该地区2018年的环境基础设施投资额的预测值为y=一 30.4+13.5×19=226.1（亿元）。

利用模型②，该地区2018年的环境基础设施投资额的预测值为y=一99+17.5×9=256.5（亿元）。

（Ⅱ）利用模型②得到的预测值更可靠。

理由如下：

（1）从折线图可以看出，2000年至2016年的数据对应的点没有随机散布在直线v-- 30.4十13.5t的上方和下方。这说明利用2000年至2016年的数据建立的线性模型①不能很好地描述环境基础设施投资额的变化趋势。2010年相对2009年的环境基础设施投资额有明显增加，2010年至2016年的数据对应的点位于一条直線的附近，这说明从2010年开始环境基础设施投资额的变化规律呈线性增长趋势，利用2010年至2016年的数据建立的线性模型y=99+17.5t可以较好地描述2010年以后的环境基础设施投资额的变化趋势，因此，利用模型②得到的预测值更可靠。

（2）从计算结果看，相对于2016年的环境基础设施投资额220亿元，由模型①得到的预测值226.1亿元的增幅明显偏低，而利用模型②得到的预测值的增幅比较合理。说明利用模型②得到的预测值更可靠。

2.考点定位与考查意图。

通过建立数学模型，解决实际问题是高考考试要求的重要内容。特别是伴随着大数据时代的到来，人们常常需要对网络、文本、声音、图像等大量信息进行数字化处理，使数学模型的研究领域与应用领域得到极大拓展，特别是随着统计与概率知识在中学数学内容的增加，为学生的数学建模提供了知识储备和解题工具。在对其考查时，可以从模型建立、检验模型等方面设置问题。在对数学建模考查时，更为注重根据题干中的精确数据构建数学模型，强调用数学知识、思想方法解决数学问题的能力，淡化对数据的分析和处理，试题以环境投资为背景，首先给出了环境基础设施投资额的折线图，旨在考查学生通过折线图进行数据分析的能力。该题重点考查数学模型建立的选择，试题的设计有利于培养学生的数学应用意识，学生领会到统计与概率的思想方法在现实生活中有着广泛的应用，形成自觉应用数学知识指导社会实践的意识，提高学生的综合实践能力。数学模型是应用数学知识解决实际问题的一种有效的工具。

3.错误原因。

不重视数学原理和数学应用，数学应用意识比较淡漠，不注重与实际的结合，难以对现实问题中的有用数据进行处理与模型构建。没有计算的耐心和准确度。

4.复习建议。

教材是学习数学基础知识、形成基本技能的“蓝本”，是高考试题的重要知识载体。纵观新课程卷中的概率统计试题，大多数试题源于教材，特別是客观题都是从课本上的练习题或习题改编的，即使是综合题.也是由教材例、习题的组合、加工和拓展而成，充分表现出教材的基础作用。复习阶段必须按《教学大纲》和《考试说明》对本部分内容的要求，以课本的例、习题为素材，深入浅出、举一反三地加以类比、延伸和拓展，在“变式”上下功夫，力求对教材内容融会贯通。

重视数学思想方法的渗透，数学思想方法作为数学的精髓，历来是高考数学考查的重中之重。它蕴含在数学知识发生、发展和应用的过程中。在概率统计的内容中蕴含着丰富的数学思想方法，概率统计为人们处理现实数据信息，分析、把握随机事件，提供了强有力的工具（计算随机事件发生的概率、求随机变量的数学期望与方差），也更加丰富、完善了中学数学思想方法，进一步拓宽了知识的应用空间。

重视概率统计的应用功能，由于新课程强调数学教育的基础性、现实性、大众性，重视素质教育与高考的兼容性，概率统计在社会现实中具有很高的应用价值。在复习中要关注生活背景、社会现实、经济建设、科技发展等各个方面，并从中提炼出具有社会价值的数学应用背景。应注意培养学生善于从普通语言中捕捉信息，将普通语言转化为数学语言的能力，使学生能以数学语言为工具进行数学思维与数学交流。

二、跟踪练习

例3 某城市为了解游客人数的变化规律，提高旅游服务质量，收集并整理了2014年1月至2016年12月期间月接待游客量（单位：万人）的数据，绘制了图2所示的折线图。根据该折线图，下列结论错误的是（ ）。

A.月接待游客逐月增加

B.年接待游客量逐年增加

C.各年的月接待游客量高峰期大致在7、8月

D.各年1月至6月的月接待游客量相对于7月至12月，波动性更小，变化比较平稳

解析：由折线图可知，8月份以后的月接待游客量减少，A错误;年接待游客量逐年增加，B正确;各年的月接待游客量高峰期大致在7、8月份，C正确;各年1月至6月的月接待游客量波动性小，变化比较平稳，D正确。故选A。

例5某工厂的某种产品成箱包装，每箱200件，每一箱产品在交付用户之前要对产品进行检验，如检验出不合格品，则更换为合格品。检验时，先从这箱产品中任取20件进行检验，再根据检验结果决定是否对余下的所有产品进行检验。设每件产品为不合格品的概率都为p（O

（1）记20件产品中恰有2件不合格品的概率为f（p），求f（p）的最大值点P0。

（2）现对一箱产品检验了20件，结果恰有2件不合格品，以（1）中确定的p。作为p的值。已知每件产品的检验费用为2元，若有不合格品进入用户手中，则工厂要对每件不合格品支付25元的赔偿费用。

①若不对该箱余下的产品进行检验，这一箱产品的检验费用与赔偿费用的和记为X，求E（X）;

②以检验费用与赔偿费用和的期望值为决策依据，是否该对这箱余下的所有产品进行检验？

分析：本题以企业在销售过程中的成本控制问题为背景，着眼于“最小化成本”的决策问题，综合考查了概率统计知识。