旋转磁场三定律与时空矢量图
(华南理工大学电力学院,广东广州 510640)
0 引言
旋转磁场与时空矢量图是交流电机理论的重要内容。然而,流行电机学文献[1]~[11]对这一重要内容的阐述,普遍存在三个缺陷:(1)没有澄清“磁场”的概念。磁场到底是一种物理实体,还是一个物理量?磁场与磁势、磁密的关系怎样?不清楚。(2)没有明确旋转磁场的一些规律到底是什么角色,是定理、定律还是仅仅是一些特点?不明确。(3)缺乏“空间”的观点。譬如,用“相轴”概念来描述空间矢量的位置,须知,“相”是一个“时间”概念。以“相量”表示时间变化量,就是证据。而且,没有阐明“相轴”与“时轴”的区别,或曰,没有阐明“相轴”的作用。又如,没有阐明“相”和“位”的区别。须知,时间相量才有“相”的概念,空间矢量没有“相”的概念,而只有“位”的概念,或曰:“相”对应于“相量”,“位”对应于“空间矢量”,也可以说,“相位”等同于“相”,但不同于“位”。
本文旨在澄清旋转磁场概念,把旋转磁场的一些规律明确归纳为三个定律,引入“空轴”概念,以克服上述三个缺陷。
说明:(1)“时间变化量”乃“随时间变化的物理量”之简。同理,“空间变化量”乃“随空间变化的物理量”之简。(2)单用“相”字乃“相位”之简。单用“位”字乃“位置”之简。(3)“空轴”乃“相绕组空间对称轴线”之简。(4)本文只讨论“圆形旋转磁势”,并简称之为“旋转磁势”。而且,只讨论基波。
1 旋转磁场概念澄清
磁场的来源有两方面:永久磁铁、电流。本文仅讨论电流所产生的磁场。
磁势的本质是电流,这一点由磁势的定义(电流乘以匝数)可以看出,从磁势的单位“安匝”也可以看出。
磁势除以磁阻得到磁通。磁通的密度称为磁密,也叫磁感应强度。
磁力线是磁场的形象表达。磁通实际是“磁力线通量”之简称。因此,磁通是表征磁场的最直观概念。但,磁通是整体(宏观)量,不能描述局部(微观)情况。因此,引入“磁通量的点密度”亦即“磁密”概念,来描述磁场在某一点处的情况(强度)。所以,磁密是真正的描述磁场强度的物理量。由于其它的原因,“磁场强度”这顶帽子被张冠李戴,给了H,而B只好命名为“磁感应强度”。然而,“磁感应强度”这个名称,名不副实。因此,学者们一般都不用,而使用“磁密”这一名称,或者,就用B。电机学文献就极少使用“磁感应强度”这一名称,而是常用“磁密”这一名称,这一点是正确的。
磁场,是一个物理实体,是一种实实在在的、有点特殊的物质。它虽然不由分子、原子组成,但,不妨碍它成为一种物质。然而,它不是一个物理量。描述磁场的物理量有:磁势、磁阻、磁导率、磁通、磁密,等。
旋转磁场,是一个旋转的物理实体。它也不是一个物理量。电机学文献中所谓的“旋转磁场”实际上指的是“旋转磁密”。这样一来,就混淆了物理实体和物理量。
因此,必须严格区分“旋转磁场”、“旋转磁势”、“旋转磁密”三个概念:“旋转磁场”是物理实体,“旋转磁势”、“旋转磁密”是描述“旋转磁场”的两个物理量。
2 旋转磁场的三个定律
描述旋转磁场的物理量有两个:旋转磁势F、旋转磁密B。
电机学中关于旋转磁势的三个规律是:(1)位置定律;(2)转速定律;(3)转向定律。
为了聚焦最核心内容,在以下各定律的陈述中,省去“对称三相绕组通以对称三相电流产生圆形旋转磁势”这种公共性、前提性的语句。
旋转磁密和旋转磁势具有一样的转速和转向。而且,当忽略铁耗时,旋转磁密B具有同旋转磁势F一样的空间位置(简称“空位”,以区别于“相位”)。
因此, 当忽略铁耗时,关于旋转磁势的三个定律,完全适合于旋转磁密。
2.1 位置定律
哪相电流达到最大,旋转磁势的正波幅就位于哪相空轴。
旋转磁势的转速与电流的频率成正比,与绕组的极对数成反比。
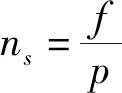
(1)
2.3 转向定律
旋转磁势的转向与三相电流的相序相同。
3 时空矢量图的一些概念
3.1 时轴与空轴
关于时轴,已有文献都已讲清楚,无须赘言。
新时代,昆楚大铁路开通运营,大理、楚雄与文山、红河4个民族自治州齐刷刷迈入高铁时代;随着广深港高铁开通,今年9月23日高铁牵手春城昆明与东方之珠香港……
关于空轴,前已说明,空轴并非“空心轴”,乃“相绕组空间对称轴线”之简。
由于每相绕组有一个空轴,因此,一共有三根空轴。
3.2 投影与定位
投影概念属于时间领域。相量之所以能够代表时间正弦变化量的瞬时值,正是通过相量向时轴投影来实现的。
因此,时轴存在的意义就是投影。
定位概念属于空间领域。由于磁势、磁密不是单纯的时间变化量,而是时、空变化量,因此,不能通过投影来确定其大小。或者说,空间矢量不需要投影,而需要定位。通过三根空轴根据前述“位置定律”来对空间矢量进行定位。一旦确定了旋转磁势正波幅的位置,那么,旋转磁势该瞬间在空间各点的大小也就确定了。因此,空轴存在的意义就是定位。
3.3 三时轴与三空轴
在画三相交流系统的相量图时,有两种选择,那就是:单相量三时轴法、单时轴三相量法。两种方法效果一样,但,单相量三时轴法明显优于单时轴三相量法。优点在于:可以少画很多相量,从而使图面简洁而直观。
因此,流行的电机学文献都采用单相量三时轴法。遗憾的是,几乎所有的电机学文献都没有对此给出说明,除了文献[1]。为何单相量三时轴法可以少画很多相量?这里稍微展开一下,具体阐述,请见文献[1]。
譬如,我们要画三相异步电动机的相量图。采用单相量三时轴法时,结果如图1所示。定子有三相,定子电流有三个,每相一个,为什么只画了一个电流相量?其它每一个相量都一样,都是本来三个,只画一个。为何可以这样?这就是单相量三时轴带来的好处。请注意:三根时轴统统地省略而未画出。但一定要记住:三根时轴是存在的,它们对称地分布于相平面上。当定子电流相量向定子某相时轴投影时,就得到该相电流的瞬时值。其他相量也是这样。如果采用单时轴三相量法,那么,同一个相量需要画三遍:每相一遍,共三相。图1中的相量将会多出两倍!真要画出,估计很难看清了。同步电机的相量图可作类似理解。
与时轴一样,空轴也是三根。但由于空间矢量不是属于某一相,而是属于三相整体的,所以,画空间矢量图,不存在“单空轴三矢量法”,只存在“单矢量三空轴法”。这一点,也说明了相量与空间矢量的不同。
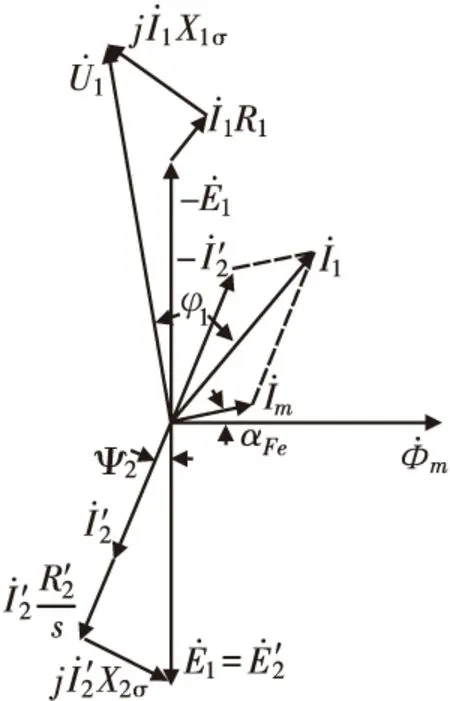
图1 三相异步电动机相量图
3.4 时间相量与空间矢量
时间相量,就是相量的意思。空间矢量则不能等同于一般的矢量。一般的矢量与正弦变化量无关。而空间矢量代表的是在空间按照正弦规律变化的物理量。它是仿照相量引入的,因为相量代表的也是按照正弦规律变化的物理量,只不过一个属于空间领域,一个属于时间领域。
但是从数学上讲,相量、空间矢量,都可以看做一般的矢量,因而平行四边形法则可以适用。
3.5 相与位
相指的是“相位”,是时间概念;位指的是“空位”,是空间概念。
当把相量、空间矢量数学化为图形时,相量和空间矢量都变为数学意义上的矢量,相和位都表现为数学上的几何位置。因为:数学是关于数与形的学问,一旦数学化,就抽去了物理内涵,再没有“时间”、“空间”等物理意义的差异了。
3.6 画时空矢量图的两个规则
为了便于研究,画时空矢量图时,一般遵循如下两个规则。
规则1:各相时轴、空轴同轴。
规则2:忽略铁耗。
据规则1和位置定律可知:电流相量与磁势空间矢量具有相同的位置(I、F同位)、磁通相量与磁密空间矢量具有相同的位置(φ、B同位)。
据规则2可知,电流相量、磁通相量具有相同的位置(φ、I同位)。
显然,由I、F同位和φ、B同位以及φ、I同位,可以推出F、B同位。
最终,属于同一主体(定子)的I、F、φ、B俱同位。如此,给画图和研究带来莫大方便。
当然,对同步机转子而言,只有F、φ、B具同位。因为转子励磁电流为直流,没有相量可言。还有,为了方便,这里的符号全部省去了表示相量、空间矢量的帽子标记。
4 结语
4.1 本文澄清了旋转磁场相关的一些概念。
4.2 归纳出旋转磁场的三个规律:位置定律、转速定律、转向定律。为后学带来方便。
4.3 澄清了时空矢量图相关的一些概念:时轴与空轴,投影与定位,相与位,等。引入“空轴”,以取代“相轴”。指出时轴和空轴的不同功能:时轴用于投影,空轴用于定位。空间矢量没有“相”的概念,只有“位”的概念。

