并联机构轻量化设计
汪满新 谌秋生 刘 方 祖 莉 安守和
(1.南京理工大学机械工程学院, 南京 210094; 2.宜昌测试技术研究所, 宜昌 443003)
0 引言
并联机构因具有刚度大、结构稳定、承载能力强、精度高、运动惯性小、实时控制性好等特点而得到广泛应用[1],特别是1T2R 3自由度并联机构,如Z3主轴头中3-PRS并联机构[2],Tricept、Exechon、以及TriVariant等混联机器人中的3自由度并联模块[3-5],已在飞机大部件加工与自动钻铆、机身与机翼对接面现场加工、汽车发动机缸体销孔过盈装配,以及大型钢构相贯线切割等方面得到应用。
静刚度可表征机构在外载荷作用下抵抗变形的能力,是并联机构最重要的性能之一,因而常常被作为评价机构性能以及机构结构参数优化设计的指标。早期刚度性能优化所用刚度指标大都参考运动学性能指标的研究思路提出,即使用刚度矩阵的代数特征值[6-11]。HUANG等[6]提出以机构末端刚度的全域均值为性能指标,考察了该指标随机构截面参数变化的规律。XU等[7]与WU等[8]以刚度矩阵最小特征值为评价依据,分别对一类以3自由度并联机构为主体的抛光机及一类3自由度非对称球面并联机器人结构参数开展优化。值得指出,以上述代数特征值为性能指标所代表的物理意义与使用场景不甚清晰,且大部分仅仅局限于以某个指标为依据考察刚度在工作空间内的分布规律,而未实施基于刚度的优化设计。
刚度矩阵同时包含线刚度与角刚度,存在量纲不一致的问题。为此,学者们主要采取了2种方法:①利用特征长度对刚度矩阵作归一化处理,在刚度矩阵前乘或后乘某一矩阵,该矩阵也称为权重矩阵[12-13]。如SUN等[13]对3自由度冗余驱动机构刚度分析时,提出以刚度矩阵的特征值对刚度矩阵作归一化处理。刚度矩阵作归一化处理后其数学特征值往往和特征长度关联密切,但特征长度的选择目前暂无统一标准。PORTMAN等[14]提出共线刚度作为优化设计的刚度性能指标,通过对刚度矩阵同时前乘和后乘无穷小位移旋量得到共线刚度,包括线刚度和角刚度。②利用无阻尼振动方程中质量与刚度的关系,以得到具有齐次量纲的矩阵[15],此方法会将得到的矩阵单位转变成固有频率的单位,故优化设计无法保证机构的刚度性能。
上述刚度评价指标大部分为了使机构具有良好的刚度性能,虽可使机构具备高刚度,但是质量与体积或变大,影响机构动态特性,故在刚度设计时应兼顾机构的动态性能。固有频率作为动态特性的重要评价指标之一,常常被用于机构的优化设计[16-18]。ZHAO等[16]以有限元分析与子结构综合技术构建8-PSS并联机构的弹性动力学模型,并通过灵敏度分析了影响低阶固有频率的要素,进而为该机构的动态性能改进奠定了理论基础。ZHANG等[18]以3-RPS并联机构为对象,通过旋量理论和能量法构建其刚体动力学模型,并据此考察了机构一阶固有频率随尺度参数的变化情况。为得到低阶固有频率,以上研究工作必须先通过复杂的流程构建机构的动力学模型。
轻量化设计是指在满足机构所需刚度约束前提下,减轻机构零部件的质量,或在保持质量不变的前提下,提升机构的刚度。因此轻量化设计为在兼顾刚度的前提下提升机构动态特性的有效途径。该思路已被用于机床零部件的优化设计中,如ZULAIKA等[19]提出一种可兼顾加工效率的铣床轻量化设计方法。
1 系统简介与刚度模型
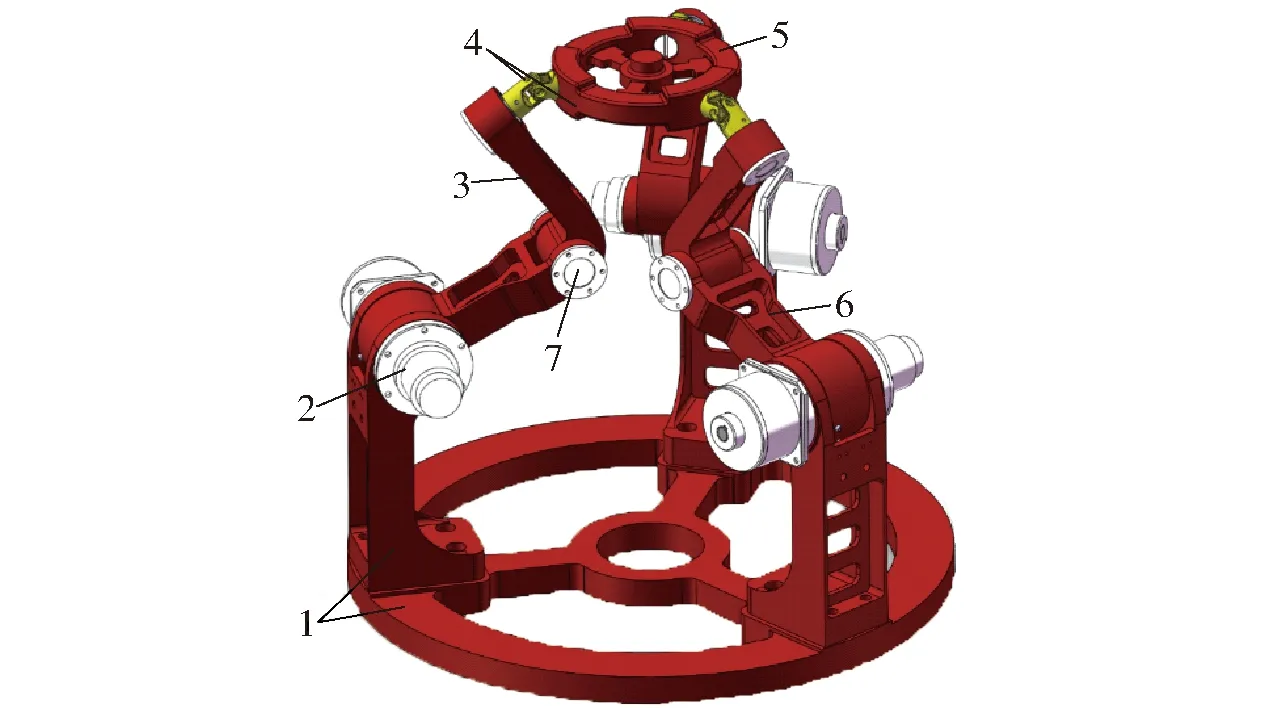
图三维模型Fig.1 3D model of parallel mechanism1.机架 2.转动副从动臂 4.球幅S 5.动平台 6.主动臂 7.转动副R
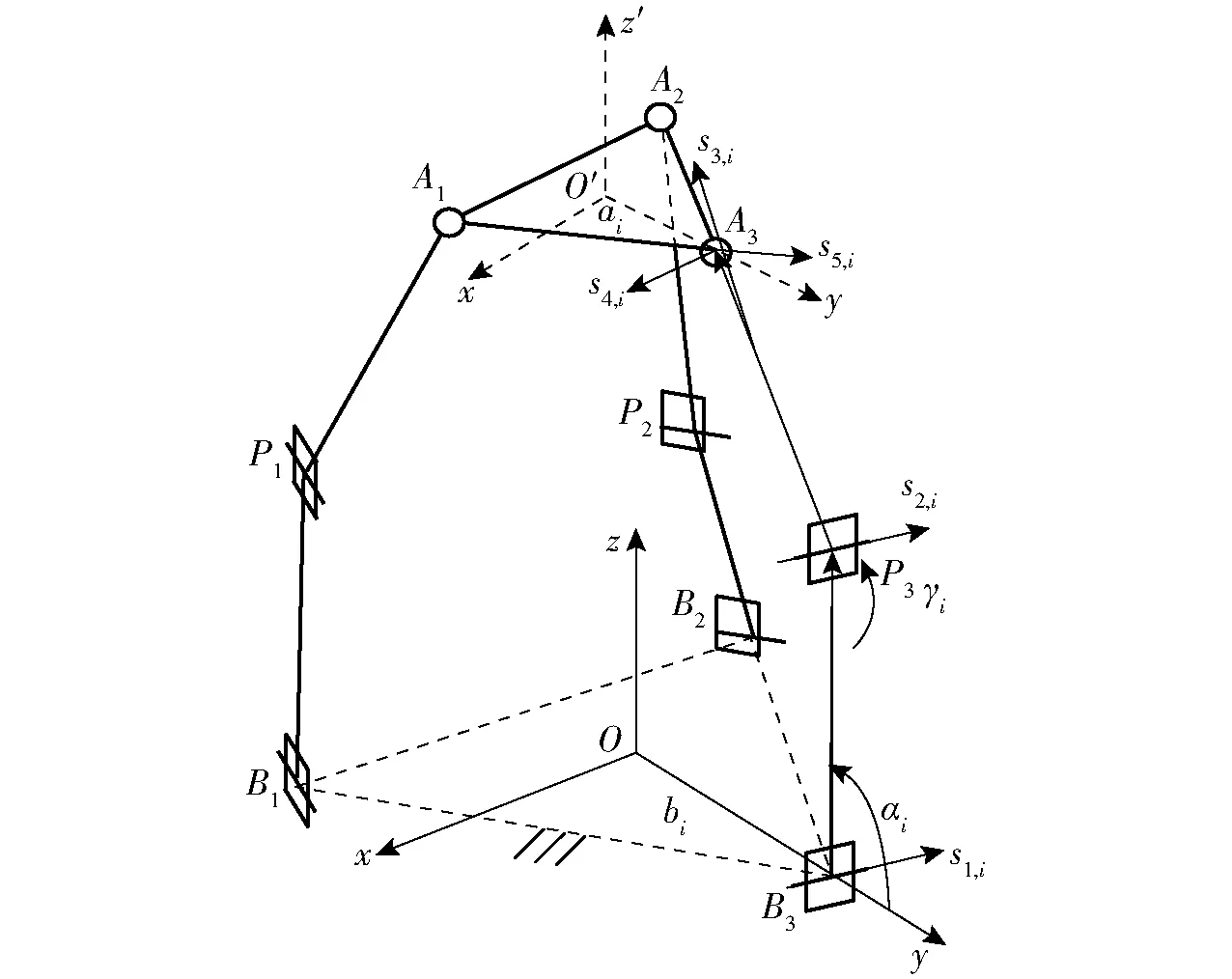
图并联机构结构简图Fig.2 Schematic of parallel manipulator
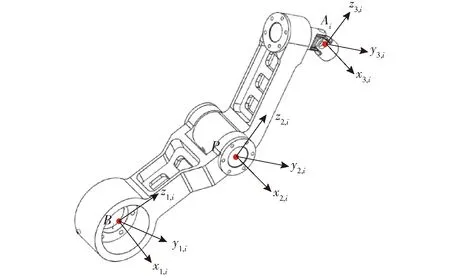
图3 支链体装配体连体坐标系Fig.3 Body fixed frames of limb body assembly
参照文献[20],在不考虑重力且假设静平台和动平台为刚体的前提下,点O′的刚度模型为
(1)
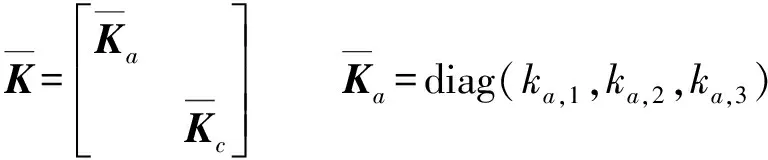
式中J——全雅可比矩阵[21]
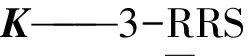
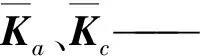
ka,i、kc,i——点Ai沿z3,i(驱动)和x3,i(约束)方向的界面刚度
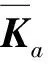
(2)
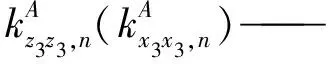
对于子装配体1,其刚度可表示为
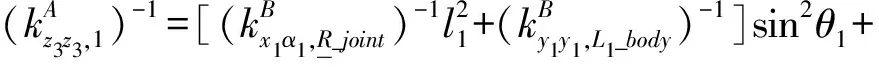
(3)
式中θ1——主动臂BiPi与从动臂PiAi间的夹角
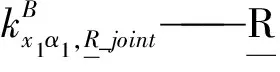
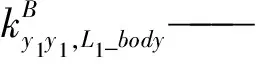

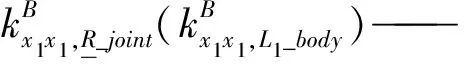
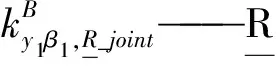
对于子装配体2,其刚度可表示为
(4)
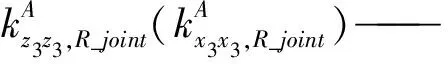
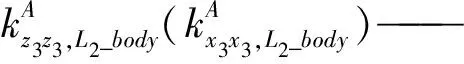
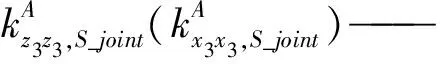
由于S副尺度参数比较小,变化幅度不大,故为简化计算,将其视为常数。

(5)
其中
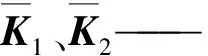
K1、K2——仅考虑子装配体1和子装配体2弹性时末端刚度矩阵
2 轻量化设计
2.1 设计变量
2.1.1子装配体1
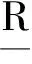
图4 主动臂L1关键结构参数Fig.4 Critical structural parameters of active link
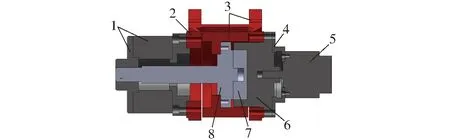
图5 转动副结构示意图1.制动器 2.机架 3.主动臂 4.减速机法兰 5.电机 6.减速机1 7.减速机2 8.旋转轴
2.1.2子装配体2
子装配体2包括球副S、从动臂L2及转动副R。现分别对他们的结构进行剖析如下:
(1)如图6所示,球副S一端由虎克铰连接于动平台,一端由自转销轴旋转连接于从动臂L2。当虎克铰的尺寸确定后,自转销轴的直径也随之确定,故球副的设计关键在于虎克铰的选型,由文献[20]可知,球副在驱动与约束方向的刚性贡献率均小于其他构件,故将在考虑构件间的尺度关联关系和整机尺寸之后,尽可能增大球副尺寸以提高其刚性。
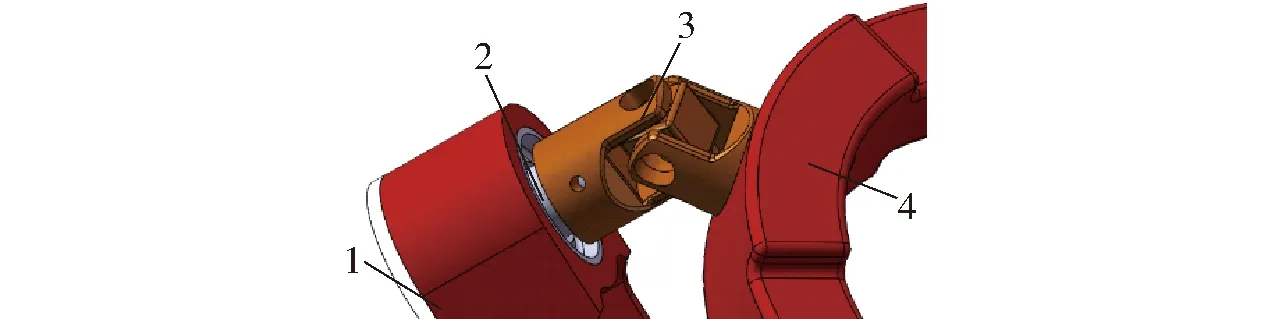
图6 球副S示意图Fig.6 Diagrams of S joint1.从动臂 2.自转销轴 3.虎克铰 4.动平台
(2)如图7所示,从动臂轴向长度较大,故影响其刚度和质量的主要因素为从动臂自身的结构参数,包括从动臂长度l2、宽度lb、高度lh以及筋板厚度lt4、lt5与lt6。其中,l2为机构尺度参数,可由运动学设计提前确定。当球副尺寸确定后,从动臂宽度lb也随之确定。此外,为保证从动臂在驱动方向的刚度分布均匀,令lt4=lt6。综上可知,从动臂的独立设计变量为lt4、lt5、lh。
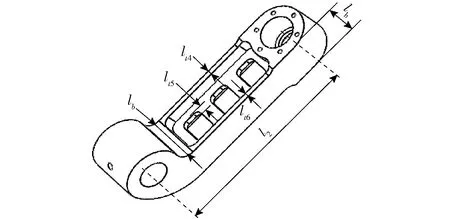
图7 从动臂L2关键结构参数Fig.7 Critical structural parameters of driven link
(3)转动副R包含旋转轴及轴承,一般轴承的刚性小于相同直径轴的刚性,故转动副R的刚性主要由其内轴承决定。由文献[20]可知,转动副R的刚性远大于其他运动部件,故设计时在考虑标准件的安装和关联部件的尺度关联关系的前提下,尽量减小设计尺寸以减小质量。
2.2 目标函数与设计流程
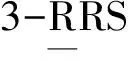
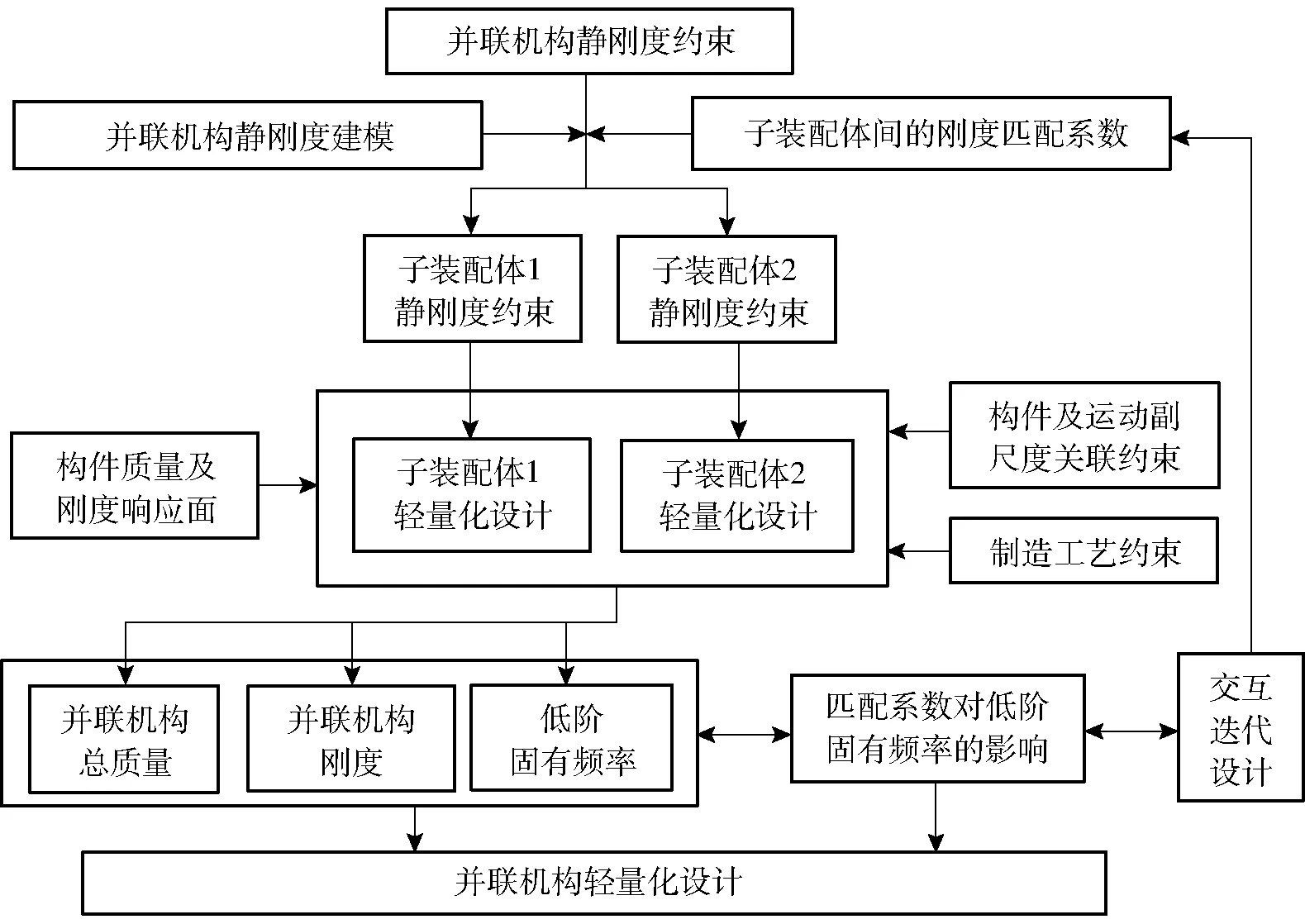
图并联机构轻量化设计流程图Fig.8 Process of lightweight design for parallel mechanism
据此,可得轻量化设计目标为
(6)
式中mk——支链的第k个子装配体的质量
f——机构低阶固有频率
2.3 刚度约束
2.3.1机构末端静刚度约束
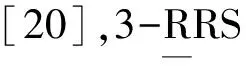
(7)
考虑机构常用的工作范围,令60%工作空间(θ=0~18°,ψ=0°~360°)内上述各向线刚度和角刚度满足
(8)
式中 [ku]、[kv]、[kw]——各线刚度在60%工作空间内的下限值
[kru]、[krv]、[krw]——各角刚度在60%工作空间内的下限值
2.3.2刚度匹配准则
由力学原理可知,对于串联弹簧系统,其刚度由系统内刚度最薄弱的子系统决定。故在总质量一定的前提下,合理分配各子系统的质量和刚度,有利于在保持质量不增加的前提下大幅提升整机的刚度。为此,需制定各子系统间的刚度匹配准则。

式中ku,L1、kv,L1、kw,L1——子装配体1弹性时机构末端点沿x′、y′、z′轴的线刚度
kru,L1、krv,L1、krw,L1——子装配体1弹性时机构末端点绕x′、y′、z′轴的角刚度
ku,L2、kv,L2、kw,L2——子装配体2弹性时机构末端点沿x′、y′、z′轴的线刚度
kru,L2、krv,L2、krw,L2——子装配体2弹性时机构末点绕x′、y′、z′轴的角刚度
ηu,L、ηv,L、ηw,L——子装配体1与子装配体2之间的线刚度匹配系数
ηru,L、ηrv,L、ηrw,L——子装配体1与子装配体2之间的角刚度匹配系数
其中,[]表示对应参数的下限值。ηL,min和ηL,max为系数上、下限。
因此,为使机构静刚度能满足式(9)所给出的约束条件,可确定支链体子装配体1与子装配体2的静刚度约束为
(10)
(11)
式(10)、(11)分别给出了由刚度匹配系数确立子装配体1与子装配体2需满足的静刚度约束。刚度匹配系数的不同将导致各子装配体的刚度约束不同,从而将得出不同的设计结果,并影响机构的固有频率,因此本文将采用以使机构低阶固有频率最高为依据确定刚度匹配系数。
2.3 几何干涉分析
如图9所示,为保证3条支链的转动副R之间不发生干涉,当机构的3条主动臂均位于水平面时,转动副R的宽度hR应满足
(12)
式中lR——转动副R的半径
δ——防止干涉而预留的余量
其中,lR即其内所含轴承的外径,取决于轴承的选型;注意到R副对于从动臂而言相当于悬臂梁的固定端,故其宽度应尽可能大,为此,可取其上限值,该约束主要应用于转动副的设计。
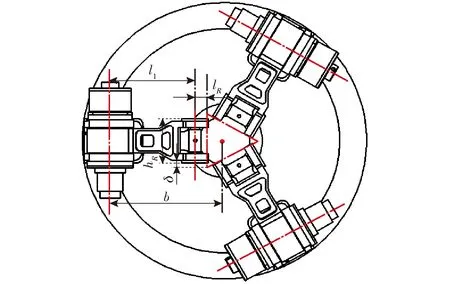
图9 干涉位形示意图Fig.9 Diagram of interference of mechanism
2.4 制造工艺约束
主动臂设计变量lt1、lt2及从动臂设计变量lt4、lt5均为壁厚尺寸,故考虑到制造工艺需满足一定要求,设置各壁厚的约束为
δmin≤lt1、lt2、lt4、lt5≤δmax
(13)
式中δmin——壁厚的最小许用值
δmax——防止壁厚过大而设置的上限值
2.5 优化设计问题构造
若支链体部件间的刚度匹配系数可以确定,则子装配体1与子装配体2之间的刚度约束即可确定。在此基础上,可根据子装配体1及子装配体2的刚度约束分别优化得出主动臂及从动臂的结构参数。然而,对于实际的工程应用,子装配体1与子装配体2的刚度并不能保证同时达到最小,因此,为保证支链体的总质量最小,在以子装配体1的刚度约束优化得到子装配体1的优化结构参数之后,以整机末端刚度为约束优化子装配体2的结构参数。故可分别构造子装配体1和子装配体2结构参数优化函数为
(14)
其中
xL1=(lt1,lt2,lm)
(15)
其中
xL2=(lt4,lt5,lh)
3 算例
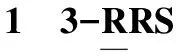
表并联机构尺度参数与60%工作空间Tab.1 Dimensions and 60% workspace of parallel mechanism
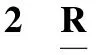
表副各项刚度Tab.2 Stiffness coefficients of joint

表3 球副中标准件选型及其刚度与质量Tab.3 Standard component, stiffness coefficients and masses of S joint

表4 R副轴承选型方案及其刚度与质量Tab.4 Standard component, stiffness coefficients and masses of R joint
在此,假设机构末端点各项刚度下限值分别为[ku]=[kv]=2 N/μm,[kw]=11 N/μm,[kru]=[krv]=2.6×104N·m/rad,[krw]=2.9×104N·m/rad。
若子装配体间的刚度匹配系数ηL可以确定,则子装配体1与子装配体2之间的刚度约束亦可确定,各子装配体轻量化设计即可完成。由式(10)、(11)可知,刚度匹配系数有6个。为简化计算,可令ηL=ηu,L=ηv,L=ηw,L=ηru,L=ηrv,L=ηrw,L。关于刚度匹配系数ηL的优选,现通过给定3种备选方案论述优选流程。
令ηL=1、ηL=0.85、ηL=0.7。则可根据式(10)和式(11)确定上述3种方案下子装配体1与子装配体2的各项刚度的下限值如表5所示。
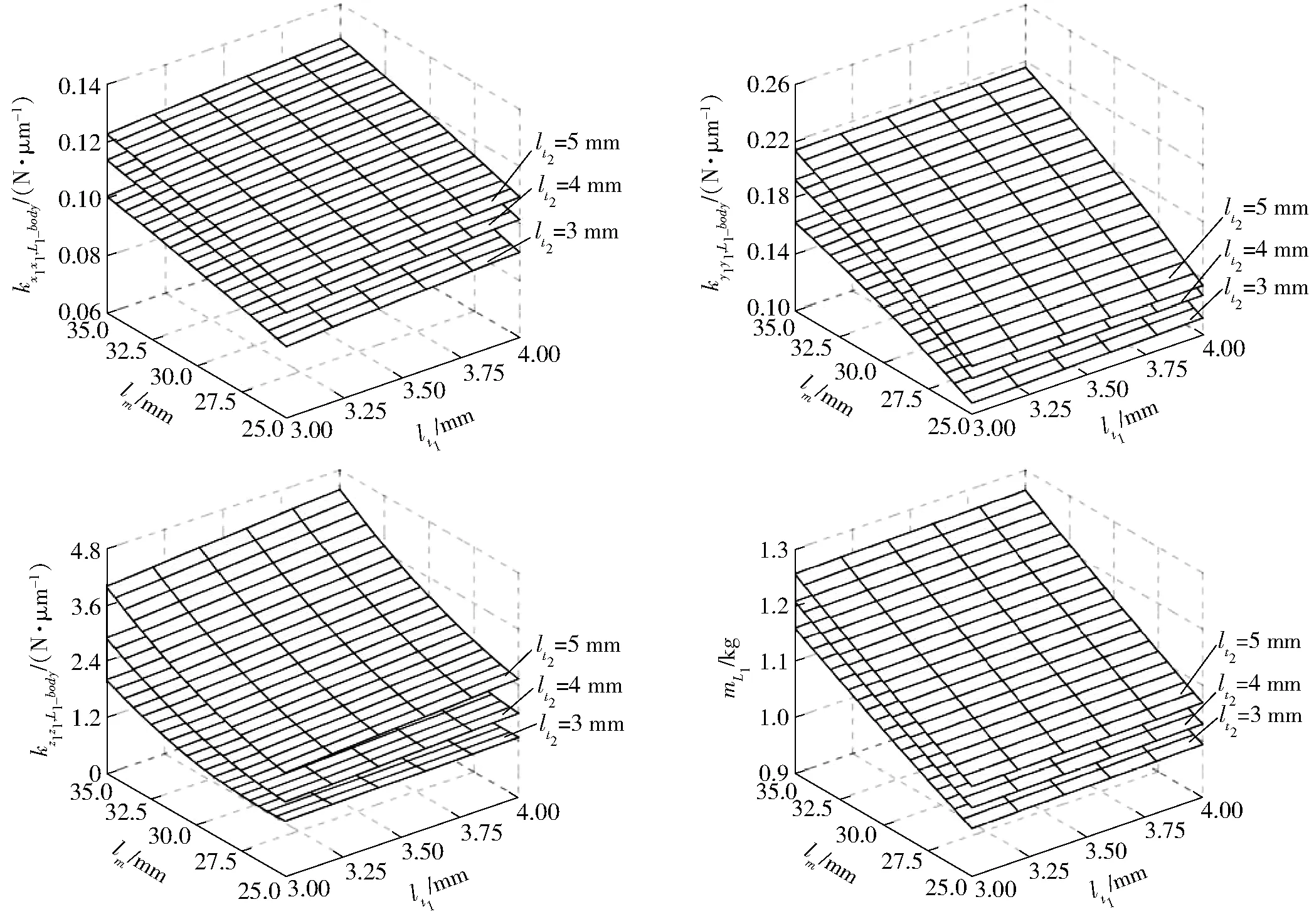
图10 主动臂L1质量与刚度响应面模型Fig.10 RSM of mass and stiffness of active link

图11 从动臂L2质量与刚度响应面模型Fig.11 RSM of mass and stiffness of driven link

ηL[kO′u,L1]/(N·μm-1)[kO′w,L1]/(N·μm-1)[kO′ru,L1]/(N·m·rad-1)[kO′rw,L1]/(N·m·rad-1)[kO′u,L2]/(N·μm-1)[kO′w,L2]/(N·μm-1)[kO′ru,L2]/(N·m·rad-1)[kO′rw,L2]/(N·m·rad-1)14.022.005.20×1045.800×1044.00022.005.200×1045.800×1040.853.720.354.81×1045.365×1044.35323.945.659×1046.312×1040.703.418.704.42×1044.930×1044.85726.716.314×1047.043×104
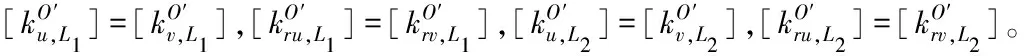
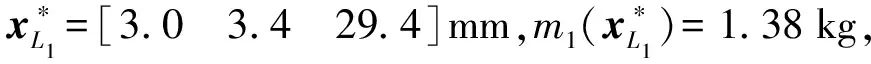
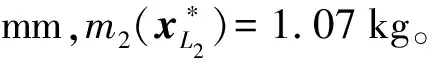
同理,使用上述相同的步骤,当ηL=0.85、0.7时对应主动臂及从动臂的结构参数如表6所示。
图12为机构末端点位于平面且在60%工作空间内的前4阶固有频率分布情况,由图可见,机构的前4阶固有频率由大至小排序依次为:f4、f3、f2、f1因此,不同方案下固有频率不同表明刚度匹配系数是影响机构动态特性的重要因素。图13为优化后仅考虑支链体装配体弹性时机构的末端点刚度的分布规律。显见,机构的全域刚度满足约束条件。

表6 3种方案下主动臂、从动臂的结构参数及其质量Tab.6 Structural parameters of active link, driven link and mass of limb-body in three cases

图并联机构60%工作空间内固有频率分布规律 (z=100 mm)Fig.12 Distributions of natural frequencies in 60% of workspace (z=100 mm)
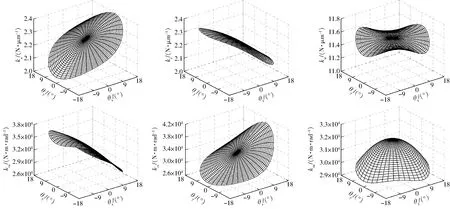
图13 支链弹性末端刚度在60%工作空间内的分布规律 (z=100 mm)Fig.13 Distributions of stiffness in 60% of workspace (z=100 mm)
4 结论
(1)提出了一种基于静刚度约束的3-RRS并联机构轻量化设计方法。该方法基于刚度匹配设计准则将末端静刚度约束分配给两个子装配体,在此基础上,考虑工艺制造及几何干涉等约束,以各子装配体的质量最小和整机低阶固有频率最高为目标完成各子装配体的轻量化设计,进而实现了整机的轻量化设计。
(2)所提出的轻量化设计方法可在满足静刚度约束条件下,使整机质量最小,且具有优良的动态特性。
(3)子装配体间刚度匹配系数的不同,对应的固有频率也不同,表明刚度匹配系数是影响机构固有频率的重要因素,为得到轻质高刚的机构,应选取合理的刚度匹配系数。

