浅谈在教学中如何培养小学生的数感
蔡丽妙
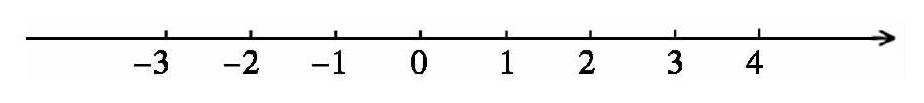
笔者所在的学校围绕《义务教育数学课程标准(2011年版)》中阐述的数感问题对全校24个教学班进行了问卷调查。调查结果发现:学生对数的认识更多源于数学计算题,而对生活中的数了解较少,习得的表示数的方法也比较单一;对100以内数的大小关系和表达把握得比较准确,而对千、万、亿级的数基本未形成数感;缺乏估算意识和估算能力。可见,学生的数感不容乐观。鉴于此,笔者就如何培养学生的数感谈谈几点看法。
一、勤用计算,培养数感
在小学阶段,计算能力是学习数学的基础,让学生在计算中感知数与数的关系,体验不同的计算方法以及根据不同的情况灵活选择策略,通过计算不断积累并发展数感,是培养学生数感的先决条件。
1. 在口算过程中培养数感。如口算下面各题,引导学生发现规律。
6.8÷0.5= 4.2÷0.25= 2.1÷0.2= 1.9÷0.1=
6.8×2= 4.2×4= 2.1×5= 1.9×10=
學生口算完,笔者让学生先进行观察,学生发现各列上下两题的计算结果相同后,引导学生从得数相同的角度去分析,让学生发现第一行各个除数乘以一个能转化为1的数,就演化为第一行被除数乘以相同的数,这样除法和乘法的结果才会相同。经常这样的训练,学生对数就有了敏锐的感觉,提高了计算速度,数感也得到增强。
2. 在估算中培养数感。教师要善于利用生活情境,让学生利用自己的生活经验,结合数据特点选择策略,强化学生的数据认知,渗透数感的培养。
如这样一道题,学校食堂准备购买水果,一箱苹果38.2元,一箱梨子9.6元,两箱香蕉每箱是22.8元,带100元够吗?不同的学生对这道题的解决策略不同,有的详细列算式:38.2+9.6+22.8×2=93.4(元)。有的用四舍五入法:38+10+46=94(元)。有的用估大法:40+10+50=100(元)。还有的用估小法:38+9+22×2=91(元)。这些用估算方法得到的答案都正确,笔者随后引导学生对自己的方法进行反思,让他们充分感受估算方法的灵活性与实用性,培养学生的估算意识。
3. 在简便计算中培养数感。简便计算是一种具有高级思维属性的特殊运算,它需要学生能掌握数字间的基本规律,变复杂的计算为简单计算,教师要善于借助这个特殊性来培养学生的数感。
如在计算11×66+22×17时,这道题的简便计算方法比较隐晦,数感较差的学生一般是没法立即发现的。这时笔者引导学生思考可以通过什么办法找到前后数字相同的因数,利用积的变化规律将题目转变成11×66+11×34,简便的计算方法就呈现出来了。这种富有挑战性的思考活动,不仅培养了学生灵活解决实际问题的能力,也升华了学生的数感。
二、善用对比,培养数感
对比是通过把两种对应的数量或者数量关系进行比较,进而发现数的规律,在教学中运用此方法可以丰富学生对数的认识,让学生形成认知能力,从而促进数感的形成。
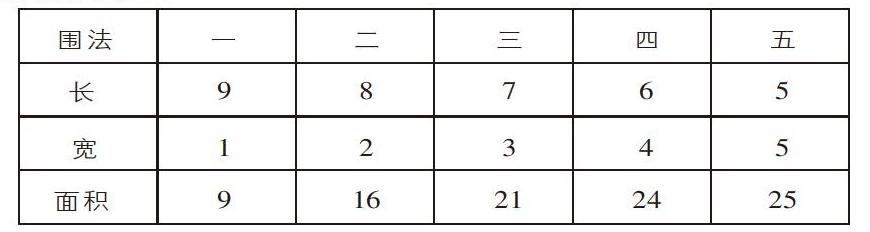
例如,用一根长20分米的铁丝围成长方形,怎样围面积最大?
这样的对比练习与表格展示,不仅增强了学生的空间想象能力,还沟通了长方形的周长和面积的关系(周长相同的长方形,形状越接近正方形,面积越大)。笔者进而引导学生通过对比表格数据,发现这样的一条规律:当两组数的和相等时,其中一组的两个数越接近,它们的积就越大。这样的题目,可以将学生静态的学习变为动态的探索,学会多角度地观察问题,不仅内化了新知,而且促进学生的数感发展。
三、巧用假设,培养数感
小学生的认知思维广度与深度还存在一定的局限性,遇到题目中的条件较为模糊、问题较为复杂等情况时,用常规的方法往往很难解决。这时教师可以有意识地引导学生通过假设数据来找到解决问题的突破口,达到问题解决和训练学生数感的目的。
例如,已知A的 等于B的 ,那么请比较A和B哪个大?教师就可以引导学生用假设法进行解答。
解法一:假设它们相等且都等于1,可以求出A等于 ,B等于 。所以A大于B。解法二:假设A等于1,利用它们的相等关系,就可以求出B等于 。所以A比较大。
除此之外,可以让学生进行自主举例假设,引导他们发现只要把A或者B假设为非0的某个具体数,再通过推理和计算都可以解决问题,也培养了数感。
四、智用数轴,培养数感
数轴是数的集合,具有方向性、区间性、直观性的特点,是学生理解数的有效而必要的学习素材。它能够帮助学生深入地认识数,准确地理解数与数之间的关系,为学生数感的建立起到积极的作用。
例如,在教学“负数的认识”时,部分学生受正数的迁移影响,对于负数的理解不清晰,这时可以充分利用数轴进行认知引导。
笔者在数轴上先标示出一些数,然后让学生观察数轴,讨论该数轴有什么特点。生1:以“0”为分界点,右边是正数,越往右,数越大;左边是负数,越往左,数越小。生2:数轴从左往右,数越来越大,没有最大的数,也没有最小的数。生3:以“0”为分界点,左右两边对称的两个数互为相反数。
在这一教学环节中,笔者把数轴作为认识数的最直观工具,充分利用数轴的直观性、区间性、方向性,让学生经历观察、交流、发现的过程,最后达到“脑中有图、心中有数”,大大促进学生数感的提升。
五、活用生活,培养数感
教师要善于搭建运用知识的平台,让学生在解决问题的过程中,学会用数学的眼光去看待具体问题,学会用数学的观点和方法来处理和解释问题。
例如,食品公司原有三种包装的价格,1升装为16元,2.5升装为36元,5升装为68元,公司计划推出“2升装”的食用油,请为“2升装”食用油定一个合理的价格,并说出理由。
学生通过计算得出:1升的单价是16元,2.5升的单价是14.4元,5升的单价是13.6元,发现随着质量的增加,单价越便宜;因此得出2升的单价应在1升的单价和2.5升的单价之间,也就是14.4元至16元,所以2升的价格差不多在28.8~32元之间。
这类既有现实意义,又具有挑战性的题目,让学生在解决实际问题的过程中,学会用数学的方法思考问题,感受数学的作用,又优化了学生的数感。
总之,数感的培养需要教师创造性使用教学素材,灵活选用教学方法,让学生学会用数学的思维想问题,用数学的方法去分析和解决实际问题。
(作者单位:福建省厦门市同安区第二实验小学)

