极不平衡桥梁转体球铰设计方法
肖宇松,陈银伟
(中铁武汉勘察设计研究院有限公司,湖北武汉 430074)
常规转体中球铰受力大致平衡,处于较均匀受压状态[1-2],而极不平衡转体球铰顶部梁体存在转角,球铰处于偏压状态且有一定偏移,若球铰间隙设置不当,可能会造成挤压,使得施工中无法转动球铰,因而极不平衡转体球铰的设计尤为关键[3-5]。
武汉市常青路主线高架桥工程为城市快速路,需跨越京广铁路汉口联络线、沪蓉线、汉丹铁路。由于铁路的红线控制范围在70 m 左右,中间9 股道铁路线间距为5 m 左右,股道中间不满足设立桥梁的条件。因此为保证施工期内铁路的运营安全,尽量减少桥梁维修对铁路的运输干扰,主桥采用(95+105)m 连续钢箱梁方案,桥面总宽51 m,使用转体施工方法跨越铁路。该桥位于市中心,若采用常规的对称转体施工方法,在转体过程中会造成巨大的拆迁成本。综合考虑场地控制因素,采用极不平衡转体施工方案,其中短侧梁体的转体长度为43.8 m,长侧梁体的转体长度为91.4 m。
由于转体两侧梁体长度相差过大,采用短臂侧配重方法难以解决转体平衡问题。因此,中铁武汉勘察设计研究院提出了一种极不平衡自控转体技术。根据现场条件,在转体的长臂侧设置临时支撑系统并配合短臂侧配重来共同实现平衡转体的目的。该项新技术开拓了桥梁转体设计、施工的新思路,能极大地突破狭窄场地条件对转体施工的制约,具有很高的经济效益和社会效益。
1 极不平衡桥梁转体施工方法
极不平衡桥梁转体施工如图1所示。在长臂侧设置圆形的轨道梁,在梁体与轨道梁间增加可以沿轨道梁行走的小车,为梁体提供可移动的竖向支撑。同时在短臂侧根据场地、轨道梁基础的承载力合理施加配重,然后进行转体作业,见图2。

图1 极不平衡转体施工示意

图2 转体完成时桥梁立面
极不平衡桥梁转体施工方法计算简图见图3。其中:L1和L2分别为转盘两侧长臂、短臂的长度;L3为轨道梁与转盘球铰中心间的距离;G为短臂侧的压重。L3值的大小取决于场地条件。转体过程中,C点的竖向位移过大会影响桥下列车的正常运行。压重G直接影响球铰处梁底的转角和B点梁体作用于轨道梁的竖向荷载。

图3 极不平衡桥梁转体施工方法计算简图
2 球铰处梁体转角的计算
采用MIDAS/Civil 2013 建立常青路主线高架桥转体施工模型,见图4。全桥共119 个单元,116 个节点,L1=91.4 m,L2=43.8 m,L3=23.6 m。球铰处的桥塔和拉索为防止横向应力过大设置了临时结构。

图4 常青路主线高架桥转体施工模型
主要控制参数与配重的关系见表1。可知,随着压重的增加,轨道梁处的反力急剧减小,球铰处的支座反力急剧增大,球铰顶部梁体的转角线性增大。压重对C点竖向位移影响不大。当压重为3 186 t 时,临时支撑B点反力为0。综合考虑临时支撑系统的承载能力,短臂侧的压重采用2 268 t。
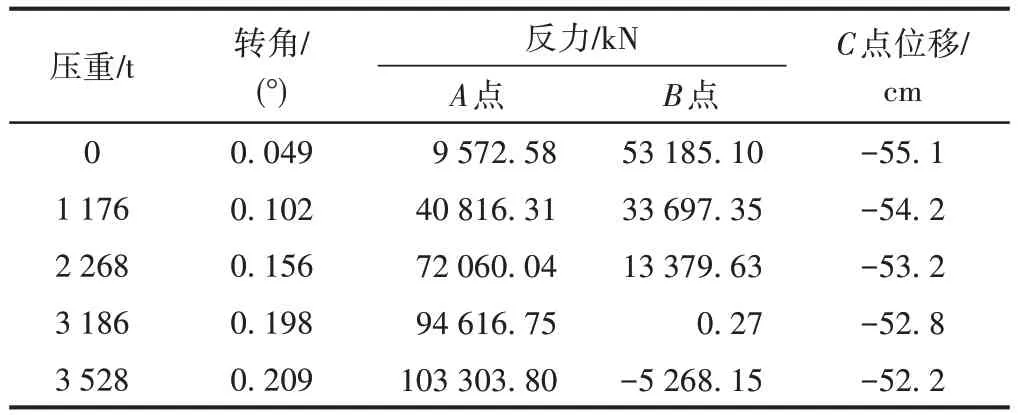
表1 主要控制参数与配重的关系
3 球铰的设计
3.1 球铰设计转角的确定
对平衡转体施工球铰设计的相关研究较多[6-10],本文重点研究平衡转体施工中球铰的设计转角。常青路主线高架桥工程转体施工中所采用球铰结构如图5所示。
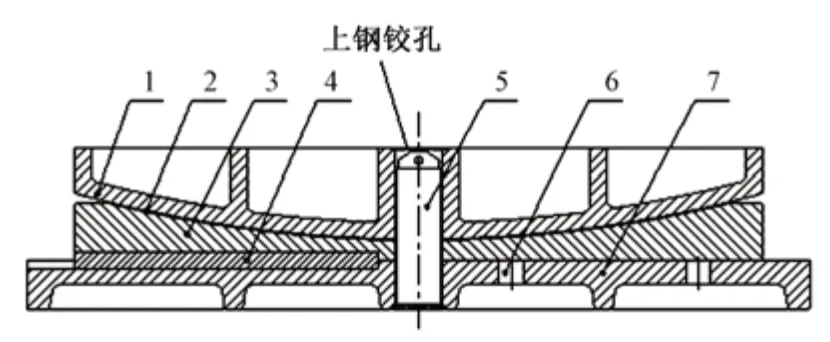
图5 球铰结构(中心线左右为不同剖面处的结构)
对于对称桥梁转体施工来说,由于球铰顶梁底的转角为0,因此,上钢铰在转体过程中仅发生绕销轴的转动,在其他方向不会发生位移。然而,对于非对称桥梁转体施工来说,由于球铰上方梁底转角的存在,上钢铰转体时除绕销轴的旋转外,还会发生绕下钢铰的面内转动。因此销轴与上钢铰间应预留足够的间距,防止因上钢铰的面内转动而使销轴与上钢铰孔的内壁接触卡住球铰,或导致销轴剪断。球铰顶部梁底的转角越大,销轴与上钢铰间预留的间距就越大。
不平衡桥梁转体施工中球铰的受力简图如图6所示。

图6 球铰受力简图
其平衡方程为
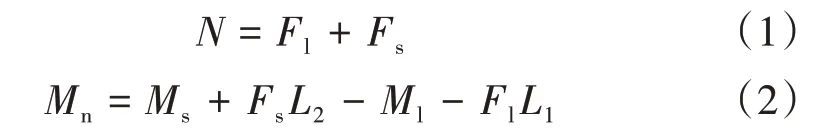
式中:Ml,Fl分别为长臂侧的弯矩、剪力;Ms,Fs分别为短臂侧的弯矩、剪力;Mn,N分别为球铰对梁体的摩擦矩和竖向反力;θ为球铰顶梁体的转角。
球铰对梁体的摩擦矩Mn与梁体发生转角的方向相反。Mn越大θ就越小。计算球铰处梁体转角时,模型中未约束球铰顶部梁底的面内转动位移(Ry),即认为Mn=0,因此计算得到球铰顶部梁体的转角会大于实际值。由于球铰的受力较为复杂,很难精确计算摩擦矩Mn,而上下钢球铰之间的摩擦板的摩擦因数很小(通过试验测试可知,应用于常青路主线高架桥转体施工的球铰摩擦板摩擦因数为0.016),可以忽略Mn的作用。因此,将模型计算的球铰顶部梁体转角作为球铰转角的设计值是合理的,且偏于安全。
3.2 非平衡转体中球铰参数确定
由于球铰上钢铰与梁体直接相连,当球铰顶梁体的转角为θ时,球铰的变形如图7所示。上钢铰以O为圆点旋转,梁体转动时球铰有A和B2个危险点。

图7 球铰转动变形示意
梁体转动时带动球铰的A点转动到A',B点转动到B'。A点到A'点需要消除上钢铰与销轴间的间距,B点到B'点则需要上下钢铰的摩擦板具有足够的弹性变形能力。因此,除常规的球铰设计参数外,不平衡桥梁转体施工中球铰还需增加2 个参数:上钢铰中心孔壁与销轴的间距D和摩擦板的最小弹性压缩量δ。由图7可知参数的简化表达式分别为

式中:γ为安全系数;r和d分别为上钢铰中心孔的半径和高度;R为上钢铰顶面的半径。
由于球铰顶部梁底的转角θ很小,在式(3)和式(4)的推导中认为弦长与弧长相等,BB'始终与OB垂直。
根据有限元分析可以发现短臂侧的压重直接影响轨道临时支撑和球铰处的支座反力,压重越大,轨道梁处的反力越小,球铰处的支座反力越大。此外,球铰顶梁底的转角也随压重的增加而增大。本文将简支模型计算的球铰顶部梁体转角作为球铰转角的设计值忽略了球铰作用于梁体的摩擦矩,是偏于安全的。
4 结论
本文以武汉市常青路主线高架桥工程极不平衡转体施工为例,介绍了通过在长臂侧增加临时支撑并结合短臂侧的压重来实现极不平衡桥梁转体的施工方法,并根据结构几何关系偏安全地推导了上球铰中心孔壁与销轴的间距和上下球铰间摩擦板的最小弹性压缩量的直接计算公式,可为类似工程设计提供参考。

