柔性中央扣对单跨悬索桥的影响分析

曾德礼

（1.中铁大桥科学研究院有限公司，湖北武汉 430034；2.桥梁结构健康与安全国家重点实验室，湖北武汉 430034）

为减小梁端纵向位移，提高桥梁的整体刚度，悬索桥通常在跨中设置中央扣。中央扣可分为刚性中央扣和柔性中央扣 2 种［1］。刚性中央扣［2］是将主缆与加劲梁联结，使跨中处的主缆和梁相对固定，如国内的润扬长江大桥和四渡河长江大桥即采用该类中央扣；柔性中央扣［3］是在跨中设置1 对或多对斜吊杆来建立缆、梁纵向约束，柔性中央扣在国内应用较多，如柳州红光大桥、贵州坝陵河长江大桥及宜昌庙嘴长江大桥等多座悬索桥均采用此类中央扣。本文以宜昌庙嘴长江大桥为背景，研究柔性中央扣对大跨度悬索桥静力及动力特性的影响。

1 工程概况

宜昌庙嘴长江大桥主桥为单跨838 m悬索桥，主梁采用钢-混结合梁，主缆桥跨布置为（250+838+215）m，中跨主缆矢跨比为1/10，矢度为83.8 m。为了改善桥梁的抗风性能，每根主缆中跨跨中处两侧附近设置2道柔性人字形中央短扣索来形成缆梁联结。扣索采用预制平行钢丝束，每根扣索由61 根钢丝组成，钢丝采用φ5.0 mm 镀锌铝合金高强钢丝，钢丝强度为1 770 MPa，全桥共8 根扣索。庙嘴长江大桥主桥立面布置如图1所示。

图1 庙嘴长江大桥主桥立面布置（单位：m）

2 计算模型

为研究柔性中央扣对悬索桥受力特性的影响，利用MIDAS有限元计算软件，分别建立该桥实际模型和不设中央扣的模型进行对比分析。主缆和斜拉索采用索单元模拟，主梁和主塔采用梁单元模拟，为了解梁体的扭转效应，主梁采用梁格法模拟。主塔、主缆根部采用固结，鞍座处采用弹性连接，塔梁之间依照设计图纸进行横向和竖向约束。全桥共计286个索单元、6 088 个梁单元。主桥有限元计算模型如图2所示。不设中央扣索的有限元模型中将跨中附近8根扣索的索单元去掉，其他单元保持不变。文中除特别标识，模型1 表示设置中央扣的计算结果，模型2 表示不设中央扣的计算结果。

图2 庙嘴长江大桥主桥有限元计算模型

悬索桥的结构刚度大，其结构受力特性分析必须考虑重力刚度的影响。在模拟施工阶段，获得各构件的初始应力，并进行应力刚化［4］，保证桥梁理论计算成桥状态与设计成桥状态基本一致后，在此阶段进行成桥阶段结构受力分析。

3 理论分析结果

3.1 静力特性

本桥设计荷载为公路-I 级，人群荷载总体计算取值为2.875 kN/m2，对设计荷载作用下结构的位移和内力极值进行分析。

表1为设计荷载作用下大桥设置中央扣和不设中央扣结构位移极值对比分析结果。可以看出：①不管是否设置中央扣，设计荷载作用下梁体最大挠度均出现在1/4 跨附近，设置中央扣后，加劲梁挠度仅降低了0.3%，主塔塔顶偏位未发生变化，说明柔性中央扣对提高加劲梁和主塔的竖向刚度影响很小；②中央扣对梁端纵向位移影响较大，相比不设中央扣，设置中央扣后加劲梁梁端纵向位移减小了16.0%。

表1 设计荷载作用下静力计算结果 mm

相比不设中央扣，设置中央扣后跨中处加劲梁最大弯矩增量由25 602 MPa降低到了24 254 MPa，降低了5.3%；最小弯矩增量由-14 568 MPa 降低到了-14 462 MPa，降低了0.7%；主塔根部最小弯矩增量基本未发生变化；跨中吊杆最大索力增量由536 kN 降低到了513 kN，降低了4.3%。

3.2 动力特性

结构动力特性的计算方法一般有子空间迭代法、多重Ritz向量法及Lanczos 算法［5］。3种算法的计算精度大致相当，只是Lanczos 算法在运算量和存储量上有所优化，计算速度更快。利用Lanczos 算法获得该桥前100 阶自振频率，并选取主梁侧弯、竖弯、纵飘及扭转等振型进行分析，分析结果见表2。表中：f1为设置中央扣的模型计算频率，f2为不设中央扣的模型计算频率，差值=（f1-f2）/f2。

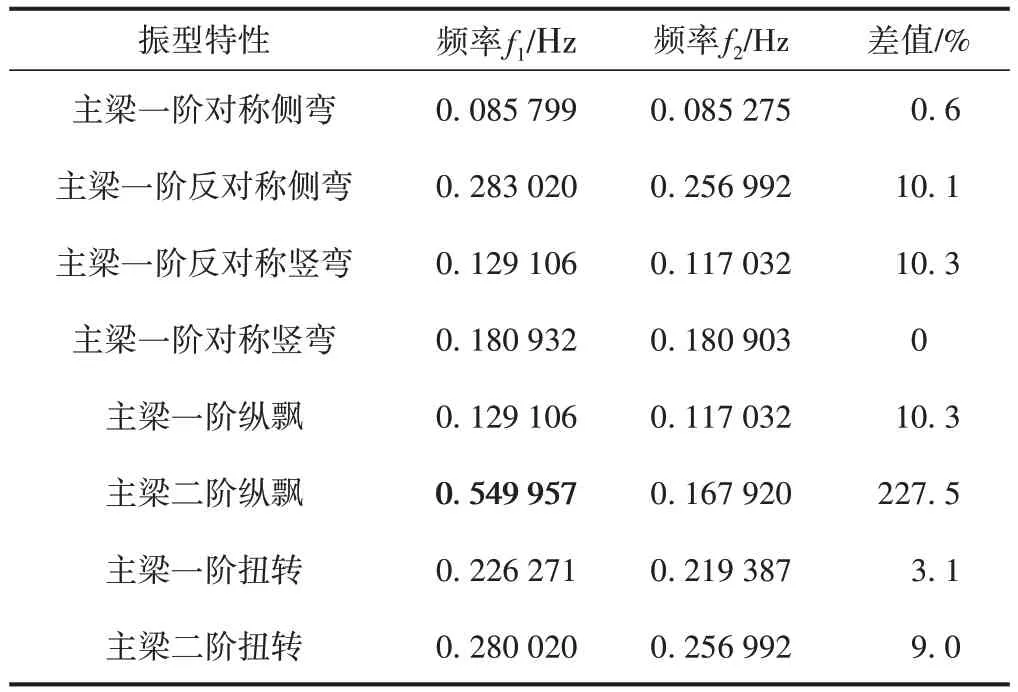
表2 桥梁自振频率计算结果

通过对比分析得出以下结论：

1）不管是否设置中央扣大桥前2 阶振型一致，其中基频为主梁一阶对称侧弯，2 阶振型为主梁一阶反对称竖弯（见图3）与纵飘同时出现，符合悬索桥柔性结构的一般规律［6］。设置中央扣时3 阶振型为主梁一阶对称竖弯，不设中央扣时3 阶振型仍为主梁反对称竖弯，主梁反对称竖弯出现了2 次，对称竖弯延迟到4阶出现，这主要是由于两侧主缆不对称造成的［7］。

图3 主梁一阶反对称竖弯（0.129 106 Hz）

2）设置中央扣后桥梁各阶自振频率均有所增大，但结构基频仅增大0.6%，说明中央扣对单跨悬索桥的整体刚度影响较小。

3）设置中央扣后主梁一阶纵飘对应的自振频率增大了10.3%，二阶纵飘出现的自振频率显著增强，且出现阶次由3 阶滞后至26 阶，说明中央扣能有效抑制加劲梁的纵飘。设置中央扣后主梁一阶对称竖弯未发生明显变化，而主梁一阶反对称竖弯增大了10.3%。这主要是因为主梁一阶反对称竖弯与主梁一阶纵飘的振型同时出现，主梁一阶纵飘振型受中央扣的抑制而增大后，主梁一阶反对称竖弯的自振频率随之增大，并不能说明中央扣能显著提高主梁竖向刚度。

4）设置中央扣后，主梁一阶扭转频率和二阶扭转频率分别增大了3.1%和9.0%，说明中央扣能提高桥梁的抗扭刚度，有利于提高梁体的抗风稳定性［8］。

4 成桥荷载试验结果

4.1 静载试验结果

静载试验主要依照JTG/T J21-01—2015《公路桥梁荷载试验规程》中关于悬索桥加载工况及测试内容的要求实施。考虑本桥的结构受力特点及加载时的结构安全，对各工况的加载效率适当予以降低。荷载试验实施时，加劲梁最大挠度、最大弯矩、梁端最大纵向位移、吊杆最大索力增量等主要加载工况的加载效率控制在0.80～1.00。主塔塔顶最大纵向偏位加载、主塔最大弯矩加载等工况的加载效率控制在0.50～0.80［9］。庙嘴长江大桥主桥静载试验的主要测试结果见表3。可知：

1）在试验荷载作用下，加劲梁挠度和塔顶偏位受中央扣影响较小，计算值相差不足0.1%。试验时加劲梁最大挠度校验系数在0.90～1.00，主塔塔顶偏位校验系数为0.90，实测值与计算值吻合较好。

2）在试验荷载作用下，设置中央扣后梁端最大位移和跨中吊杆索力分别减小了15.1%和4.8%。相比模型1 和模型2 的计算值，梁端位移实测值的校验系数分别为0.93和0.79，跨中吊杆索力增量实测值的校验系数分别为0.93 和0.89，实测值与模型1 的计算值更接近。

表3 静载试验主要测试结果

4.2 动载试验结果

庙嘴长江大桥主桥振型复杂，前10阶振型包含了主梁/主缆的侧弯（2阶）、竖弯（3阶）、扭转（3阶）、纵飘（1阶）及主塔的纵弯（1阶）等振型，测点布置时结合大桥自振频率及对应的振型进行布置。在主缆1/4 跨、跨中及3/4跨布置竖向、横向共计12个拾振器，在加劲梁的8 分点布置竖向、横向、顺桥向共计16 个拾振器，在主塔塔顶布置2 个顺桥向拾振器和2 个横桥向拾振器，全桥共计布置了32 个拾振器，如图4所示。拾振器采用991B 型超低频拾振器，实现超低频（低至0.072 Hz）大位移振动测量。

图4 主桥脉动试验测点布置示意

在全桥全封闭环境下进行脉动试验，对各测点的测试结果进行自谱、互谱分析［10］，得出大桥的前10 阶实测自振频率及振型，见表4。实测各阶振型与模型1的计算值一致，各阶自振频率实测值均大于理论计算值，说明实桥的动力刚度满足要求。

表4 脉动试验测试结果 Hz

5 结论

本文以宜昌庙嘴长江大桥为背景，对柔性中央扣对大跨度悬索桥受力的影响进行分析，得出如下结论：

1）柔性中央扣对单跨悬索桥的加劲梁挠度、主塔塔顶偏位影响较小，只能略微提高结构整体刚度，但对减小梁端纵向位移，降低跨中吊杆索力的作用明显。

2）柔性中央扣对提高主梁纵飘、加劲梁扭转频率，增大相应频率出现的阶次有一定的作用，有利于提高桥梁的抗风稳定性，同时也能减小主梁竖弯振型出现的频率。