基于改进遗传算法的区域水资源优化配置

杜丽娟

(中国地质大学(武汉) 机械与电子信息学院，武汉 430074)

1 概 述

水资源作为一种战略性经济资源，其重要性不言而喻[1]。随着城市化的快速发展，城市水资源供需矛盾日益加剧，水资源优化配置方面的相关研究显得尤为必要。水资源优化配置是指在特定区域内，对有限的、不同形式的水资源进行科学合理的分配，以满足各方用水基本需求[2]。我国水资源优化配置研究始于20世纪80年代初，从最初的宏观水资源优化配置模型研究，逐步深化到具有地区特性的多层次、多目标的水资源优化配置研究。由于区域水资源体量差异明显，同时存在多个供水单位和用水单位，使得区域水资源优化配置成为一个典型的多目标问题。孙志林[3]基于多目标非线性规划原理，提出了一种适用于多水源、多用户的水资源优化配置模型。高亮、张玲玲[4]以济宁市为例，建立了多水源多用户水资源优化配置模型，求解出不同保证率条件下优化配置结果并对其进行了水量平衡分析。通过查阅现有参考文献发现，对于多水源多用户水资源优化配置方面的研究较少涉及，多数集中在水资源相对承载力和水资源保护研究等方面。

在优化配置模型求解方面，传统水资源优化配置的优化方法每次计算只能得到一个非劣解，而采用遗传算法一次计算能得到更多的非劣解，在其中搜索确定出最优解，计算过程更为简便，结果更加精确。同时，针对传统二进制遗传算法存在的不成熟收敛、搜索效率低和参数选取困难等关键性技术难点[5]，提出了基于实数编码的多种群遗传算法。本文以都江堰灌区为例，建立多目标水资源优化配置模型，通过基于实数编码的多种群遗传算法进行求解，得到灌区水资源优化配置结果，为相关部门进行水资源调度提供科学的理论依据。

2 实数编码多种群遗传算法

实数编码多种群遗传算法是在传统遗传算法基础上进行的一系列改进补充。

首先，传统遗传算法中编码方式采用的是二进制编码，虽然易于遗传操作的实现，但其编码译码过程已经脱离问题本身，问题的自身结构特征不能得到很好的反映，存在过早收敛于局部最优并不能找到全局最优解，对于多维优化问题由于个体串位太大而造成计算量过大及过早收敛[6]。若采用实数编码，直接以原始变量数据组成个体，则可避免二进制编码译码的繁琐过程，以及过早收敛的问题。

其次，未成熟收敛作为遗传算法中不可忽视的现象，主要表现在群体中的所有个体趋于同一状态而停止进化，算法最终不能给出最优解。针对此类问题，多种群遗传算法被提出，通过引入不同控制参数对多个子种群同时进行优化搜索，通过移民算子对各个子种群进行联系，实现了多种群的协同进化[7]。在兼顾全局搜索和局部搜索的同时，其收敛速度更快，对克服未成熟收敛有显著效果。

因此，本文针对传统遗传算法存在的问题，提出了基于实数编码的多种群遗传算法，在精简遗传计算过程的同时，有效地避免过早未成熟收敛问题。

3 水资源优化配置模型的建立及求解思路

本文以都江堰灌区为例，讨论水资源优化配置模型的建立及求解思路。都江堰灌区位于四川盆地西部，由于岷江中上游地区原始森林乱砍滥伐，流域内的自然环境遭到严重破坏，水资源呈逐年减少趋势[8]。依据都江堰灌区闸首进口所处位置，将都江堰灌区划分为6个子灌区，分别为蒲阳河子灌区、柏条河子灌区、走马河子灌区、江安河子灌区、沙沟河子灌区和黑石河子灌区。以都江堰6个子灌区为研究对象，通过建立水资源优化配置模型，运用基于实数编码多种群遗传算法进行求解。

3.1 决策变量

设水资源合理配置的决策变量为：

X=(xijk)

(1)

式中：xijk为第i分区利用第j种水源向第k类用水部门分配的水量，104m3；i为分区编号，依次为蒲阳河子灌区、柏条河子灌区、走马河子灌区、江安河子灌区、沙沟河子灌区和黑石河子灌区；j为水源编号，依次为堰渠首引水、过境径流引水、当地水库蓄水和地下水；k为用水部门编号，依次为工业用水、农业用水、生活用水及生态用水。

3.2 目标函数

目标1：区域供水净效益最大

(2)

式中：aijk为i分区的j种水源向k用水部门的供水效益系数。

目标2：区域整体缺水量最小

(3)

式中：bik为i分区k用水部门的总需水量。

目标3：区域内地下水开采量最小

(4)

3.3 约束条件

1) 水资源约束。公式如下：

都江堰渠首供水量约束：

(5)

过境径流供水量约束：

(6)

当地水库全年可供水量约束：

(7)

地下水水量约束：

(8)

式中：Qqs，Qgj，Qsk，Qdx分别为第i分区的渠首、过境径流、当地水库、地下水可供水量。

2)生活需水量约束。公式如下：

i=1,2,3,4,5,6

(9)

式中：BLi为第i分区内生活需水量。

3)支渠设计流量约束。公式如下：

i=1,2,3,4,5,6

(10)

式中：Qfi为i号支渠的设计流量，m3/s；Ti为i号支渠一年的引水天数。

4)变量非负约束。

xijk≥0

i=1,2,3,4,5,6;j=1,2,3,4;k=1,2,3,4

(12)

3.4 模型求解

模型求解算法步骤如下：

1) 实数编码。本文采用实数编码，直接以原始变量构成个体。

2) 初始化种群。取种群规模为N，随机产生个体构成集合，同时保证其满足目标函数相对应的约束条件。

3) 构造适应度函数。在算法计算过程中，各子种群分别独立计算其适应度以确定优秀个体，适应度计算函数如下[9]：

Fi=a×fi+b

当fmin≥2×fp-fmax时，

当fmin≤2×fp-fmax时，

其中fp，fmax，fmin分别表示遗传当代的适应度值的均值、最大值及最小值。

4) 多种群遗传算法实现。多种群遗传算法实现步骤步骤详见文献[7]，遗传算法操作参数设定如下[5]：子群体规模取50；单点交叉概率0.9；高斯变异概率0.01；最大遗传代数50代；个体替换百分比25%；交换频率取3；移民数目为最好的5个个体。

5) 输出结果。通过判断群体是否满足收敛条件及遗传进化代数是否达到最大遗传代数，满足条件迭代终止，获得的最好个体即为具有最优解，即为优化后的各种水源为各分区在各部门的最优配水量。

4 实例计算

取都江堰灌区6个子灌区水平年2017的实际资料。以供水净效益最大、缺水量最小及地下水开采量最小为目标函数，本算例中的供水成本、可供水量和需水量等数据采用2017年水平年的实际数据。具体见表1-表3。

各子灌区工业用水净效益取28元/m3，农业用水净效益取7元/m3，生活用水净效益取3元/m3，生态用水净效益取2元/m3。优化算法成功运行10次，所得到的优化最佳配水方案见表4(第3-第6列)。相应各分区各部门水资源供需平衡分析见表4。

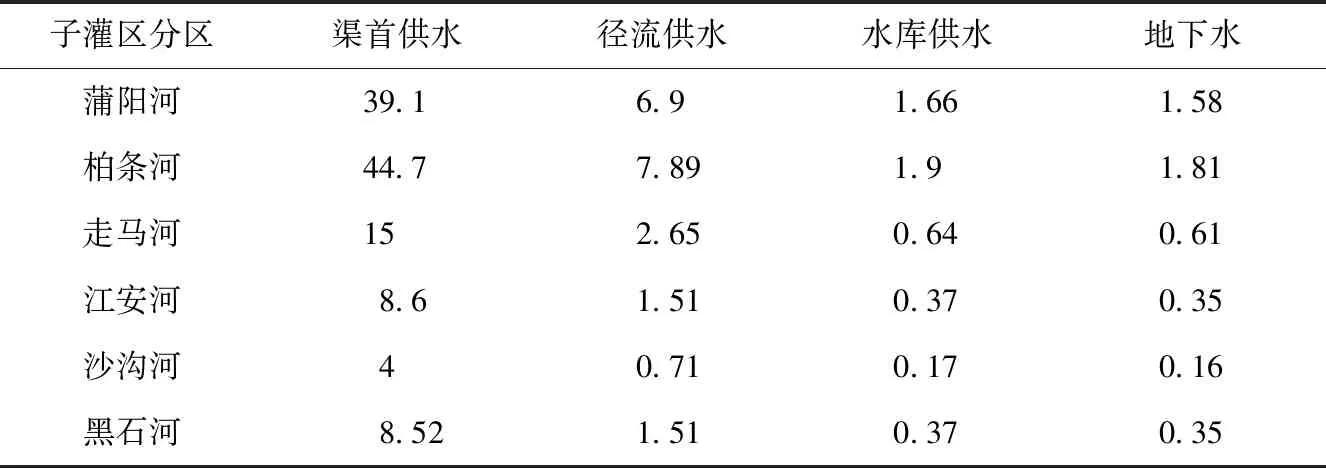
表1 各水源可供水量约束 /108 m3

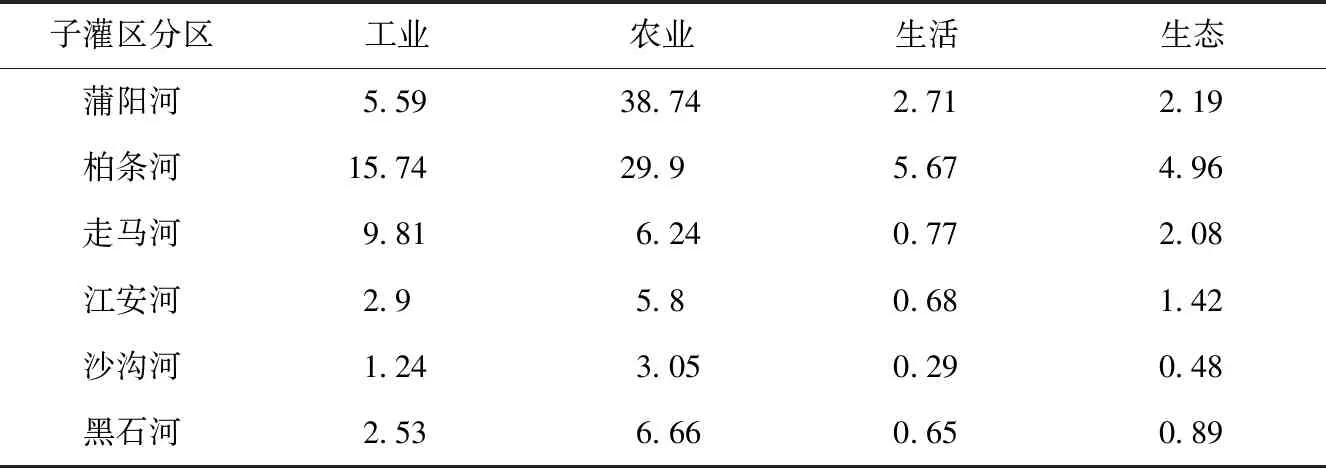
表2 各用水单位需水量约束 /108 m3

表3 支渠引水数据 /108 m3

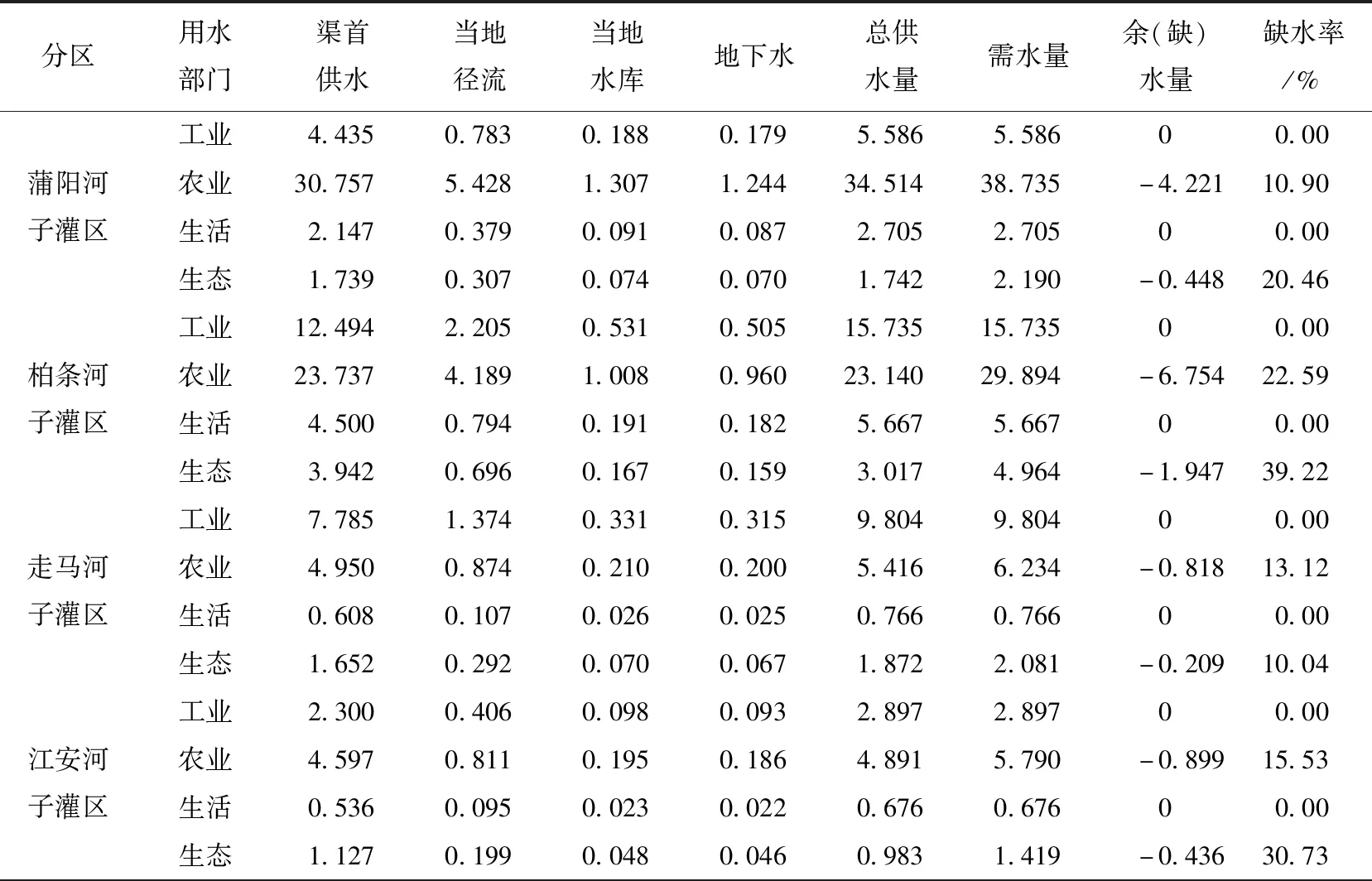
表4 各部门水资源供需平衡分析结果 108 m3

续表4

根据表4优化结果，6个子灌区中工业用水和生活用水均能得到保证，农业用水与生态用水均存在缺水情况。由于相应约束条件的限制，工业用水净效益最高，故各子灌区优化后的工业用水能够保证需要，同时也能够保证基本的生活用水满足要求。

依据优化结果显示，6个子灌区在农业用水和生态用水方面都有一定的缺口，在农业用水方面，柏条河、沙沟河和江安河子灌区缺水情况比较严重；在生态用水方面，黑石河、柏条河和江安河子灌区缺水情况严重，都在30%以上。针对各子灌区缺水情况，需要及时采取应对措施：

1) 对于农业用水有缺口的地区，需要大力发展节水农业，主要是4个方面：①农艺节水，即改进农作物结构和耕作技术；②生理节水，即培训抗旱的作物品种；③调控节水，即通过相应管理手段达到节水目的；④灌溉节水，即采用喷灌、滴灌等先进的灌溉方式。

2) 对于生态用水有缺口的地区，需要及时采取节水措施，特别是要加强工业用水的循环利用，减少水资源的占有量，工业废水也需要进行一系列污水处理措施方可排出。同时，在农业和生活方面也需要采取一定的节水措施。

5 结 论

1) 针对水资源优化配置的多目标性，综合考虑区域水资源的供水效益、缺水量以及地下水开采量等优化配置目标，同时构建需水量、供水量等约束条件，建立了一个多目标水资源优化配置模型。采用实数编码多种群遗传算法对其进行求解，解决了模型求解的问题，得到的优化配置结果验证了所建模型的合理性。

2) 针对传统遗传算法存在的早熟收敛问题，提出基于实数编码的多种群遗传算法。采用实数编码有效避免了编码译码繁琐过程，加快了计算速度。该算法中各子种群可同时进行搜寻最优解，使遗传算法全局搜索能力大大提高，避免了过早收敛现象。

3) 本文建立的水资源优化配置模型约束条件设置灵活，可根据实际情况对相关约束参数进行调整，其适用性强。