并网型多能互补系统优化规划方法

文 乐，张宝锋，张恩享，童 博，赵 勇

（西安热工研究院有限公司，陕西 西安 710054）

多能互补系统规划问题通常分为能源网架优化规划[1]、可再生能源类型选择和容量规划[2]、储能类型和容量的规划[3]3 个方面。

国内外多能互补系统研究多集中在孤网或微网领域，但国内由于能源市场化水平低、电网架设水平高等因素，并网型多能互补系统规划应受到重视[4]：一方面，电网给电力安全稳定供应提供保障，将电网作为可再生能源出力低谷时的备用电源，可减少设置、投用柴油发电机等高污染后备电源设备；另一方面，并网型多能互补的可再生能源出力可降低负荷的覆盖率要求，并根据电网峰谷电价差，从经济角度给予系统规划更宽泛的优化空间[5]。为确保并网型多能互补系统稳定、经济供能，面对已有能源网架的并网区域，可再生能源及储能类型选择和容量规划是研究重点，而类型选择与可再生能源资源禀赋、设备价格、政策补贴等各类因素有关[6]。本文从多能互补系统规划的约束条件和目标函数出发，结合粒子群算法，提出了一种经济效益最优化的多能互补系统优化规划方法。

1 多能互补系统优化规划模型

多能互补系统优化规划是以1 h 为步长、以1年8 760 h 的负荷数据进行计算分析，解决1 个满足多约束条件的单目标优化问题。

1.1 约束条件

1.1.1 装机约束

可再生能源设备容量受安装面积限制：

式中：a为可再生能源设备数量；Sa为考虑预留间隙、空间遮挡等因素的现场实勘可用于安装设备的面积；Su为单个设备安装面积。

1.1.2 功率约束

可再生能源、储能的输出功率PR、PS为

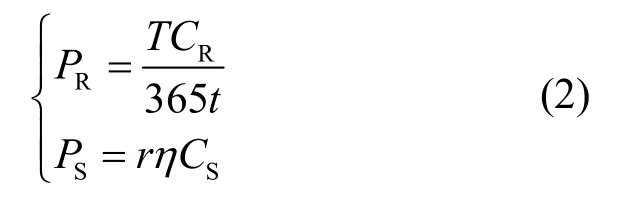
式中：T为可再生能源设备的等效利用小时数；CR、CS分别为可再生能源、储能装机容量；t为可再生能源平均日发电小时数；r为充放能倍率，表示储能设备在1 h 内可充或可放的能量最大值占储能总容量的百分比；η为储释能效率，表示储能设备的可输出能量与输入能量的比值。

可再生能源及储能功率约束为

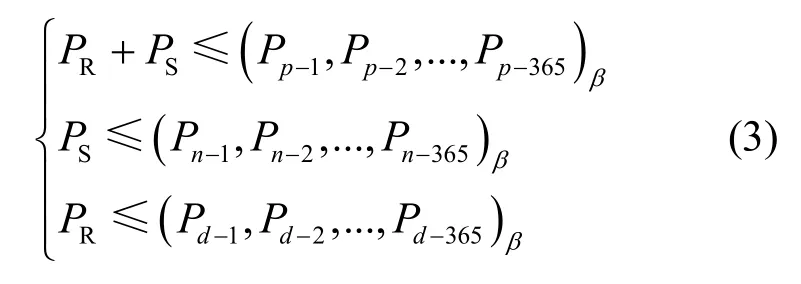
式中，(Pp–1,Pp–2,…,Pp–365)、(Pn–1,Pn–2,…,Pn–365)、(Pd–1,Pd–2,…,Pd–365)分别表示每天的第1 个电费高峰时期、第2 个电费高峰时期、非电费高峰时期的负荷每小时均值数列，β表示数列的第β百分位数。

1.1.3 可再生能源渗透率约束

可再生能源渗透率fR为可再生能源输出功率PR满足每小时负荷PL的比例，每小时的可再生能源渗透率数列为

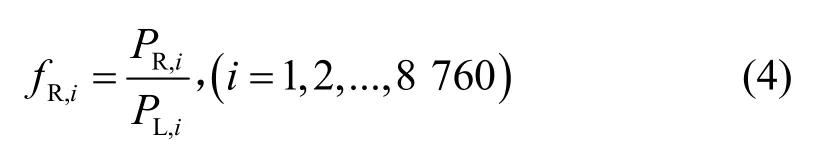
以式(4)数列的第百分位数为特征参量(fR,)，其应满足约束条件

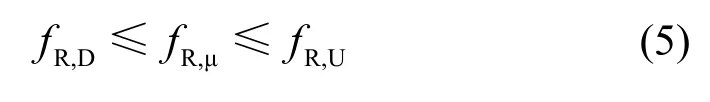
式中：fR,D为可再生能源渗透率下限，其表示在区域内可再生能源资源禀赋情况下的可再生能源渗透率期望；fR,U为可再生能源渗透率上限，其表示考虑电压、谐波等稳定因素以及电网或政策要求的可再生能源渗透率期望。

1.2 目标函数

多能互补优化规划的目标，是尽可能在高可再生能源渗透率下合理配置可再生能源及储能容量使得区域内能源消费成本最低。用年化成本cY来表示多能互补系统寿命周期内主要设备的平均每年花费成本，即

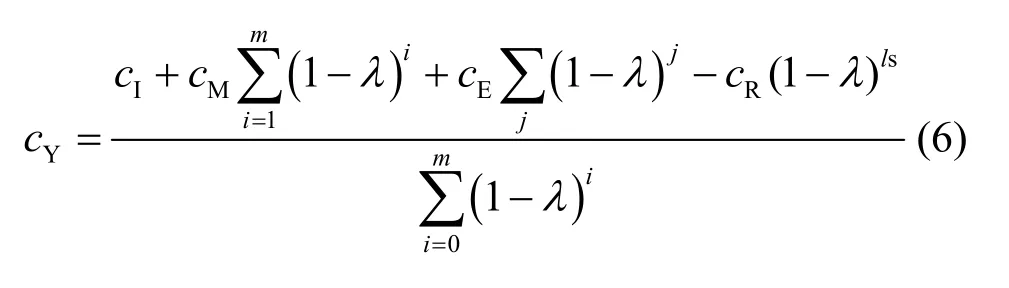
式中：cI为初投资，是可能与容量相关的线性或非线性函数；cM为每年耗费的运维成本；ls 为多能互补系统寿命；λ为折现率，表示预期收支折算成等值现值的比率；cE为第j年的子设备替换费用，cR为m年结束时的设备残值。

并网型多能互补系统的收益I体现在应用多能互补系统后减少的电网电费和可再生能源余电上网的补贴收益之和，即

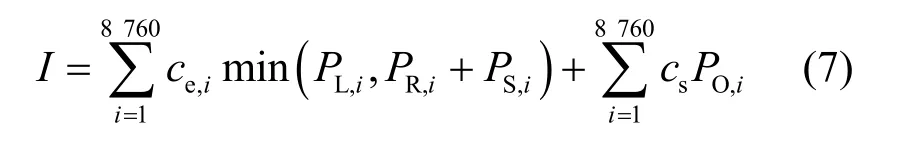
式中，ce为电网逐时电费，cs为可再生能源上网补贴价格，PO为可再生能源逐时上网功率。

当式(3)中的发生变化时，会影响光伏和储能的容量选取：当β值较大时，可再生能源和储能容量增大，其功率能够满足区域内多数逐时负荷且可再生能源余电上网获得补贴多，但也增加了多能互补系统投资成本；当β值较小时，可再生能源和储能容量减小，其功率仅能满足区域内少数逐时负荷且可再生能源余电上网获得补贴少，但也减少了多能互补系统投资成本。因此，应规划合适的可再生能源和储能容量，使得目标函数E最大化：

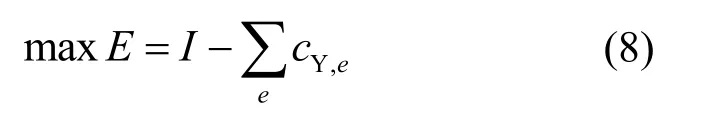
式中e表示多能互补系统中包含的各类主要设备。

2 模型求解算法

粒子群算法[7]是从随机赋值的初始粒子开始，按各粒子的移动速度和历史最佳位置计算适应度函数，使之达到最值的一种优化算法。假设维度为m的n个粒子计算适应度函数，获得使之达到最值的每个粒子的历史最优位置p和群体中所有粒子的历史最优位置g，并根据式(9)、式(10)迭代更新各粒子的速度v和位置x：

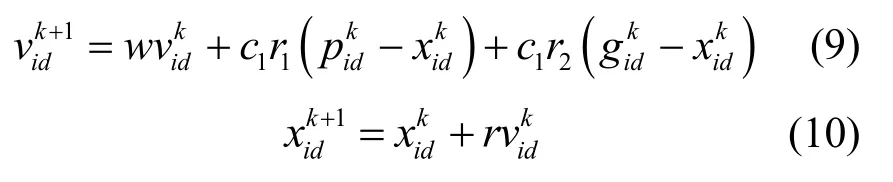
式中：角标i表示第i(≤n)个粒子；角标d表示第d(≤m)维空间；k为迭代次数，可设置阈值使迭代停止；w为惯性权重因子，表示粒子维持上一次迭代速度的程度；c1和c2为加速因子，分别表示粒子迭代倾向个体最优位置和群体最优位置的权重；r1和r2是[0,1]区间内均匀分布的随机数；r为收敛因子，表示对位置移动幅度的控制。

由于多能互补系统的可再生能源及储能类别组合多、待求解参数多，在确定设备类型选择和系统运行方式后，应用粒子群算法进行设备容量优化规划会使输出结果陷入局部最优，其原因是c1、c2及尤其是惯性权重因子w的取值影响算法的全局搜索能力和局部搜索能力[8]。一般来说，w取值越大，全局搜索能力越强而局部搜索能力越弱。

为使粒子群算法输出结果随迭代次数增长逐步逼近最优，各粒子的w值应跟随迭代次数增加而递减、并跟随其距最优粒子位置距离增加而递增，即粒子i的w值根据迭代次数和粒子位置动态变化：

式中：t为迭代次数，tmax为迭代次数阈值；wmax、wmin分别为预设的权重最大值、最小值；lg,i为第i个粒子到g的欧氏距离；lmax为预设的最大距离，当lg,i≥lmax时w(t)=wmax。

模型求解算法的具体流程如图1所示。

3 算例分析

北方某旅游度假园的负荷主要为空调、厨房、照明等。用能现状为：开采地热水满足生活热水和冬季供暖的基础负荷，利用电网电能驱动地源热泵满足夏季供冷和冬季补充供暖；消费能源主要是电能。2 台容量为1 000 kVA 的10/0.4 kV 变压器与电网连接。6月—8月为用冷负荷高峰，12月—2月为用热负荷高峰，全年负荷低谷出现在春秋两季。2018年，月均用电负荷为251 295 kW·h，极差为217 910 kW·h，全年电费为261.36 万元。典型日用电负荷如图2所示。

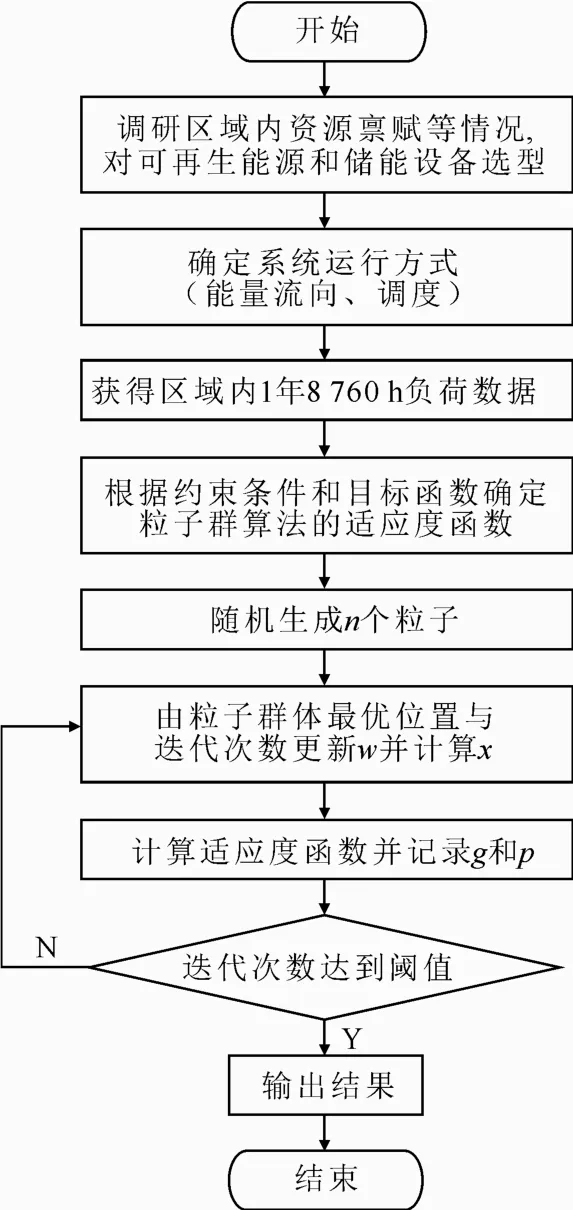
图1 模型求解算法流程Fig.1 The flow chart of model solution algorithm

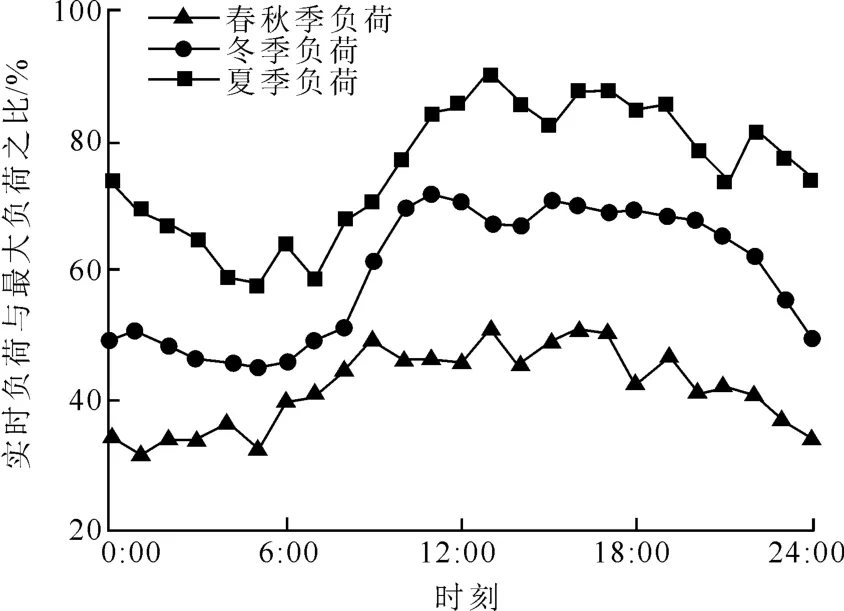
图2 典型日用电负荷Fig.2 The typical daily electricity load

多能互补系统优化规划总体思路：1）以经济用能为目标，使目标函数E最大化；2）尽可能利用可再生能源，提高可再生能源渗透率fR；3）紧跟补贴政策，把握新技术应用的机遇窗口；4）尽可能减少能源转化，宜电则电、宜热则热，实现能源梯级利用，提高综合用能效率；5）合理配置储能容量，增强多能互补的稳定性和经济性。

可再生能源及储能类型选择见表1，选择太阳能光伏发电、蓄电池储电、蓄水罐储冷热这3 类系统及设备，优化模型的主要参数见表2。

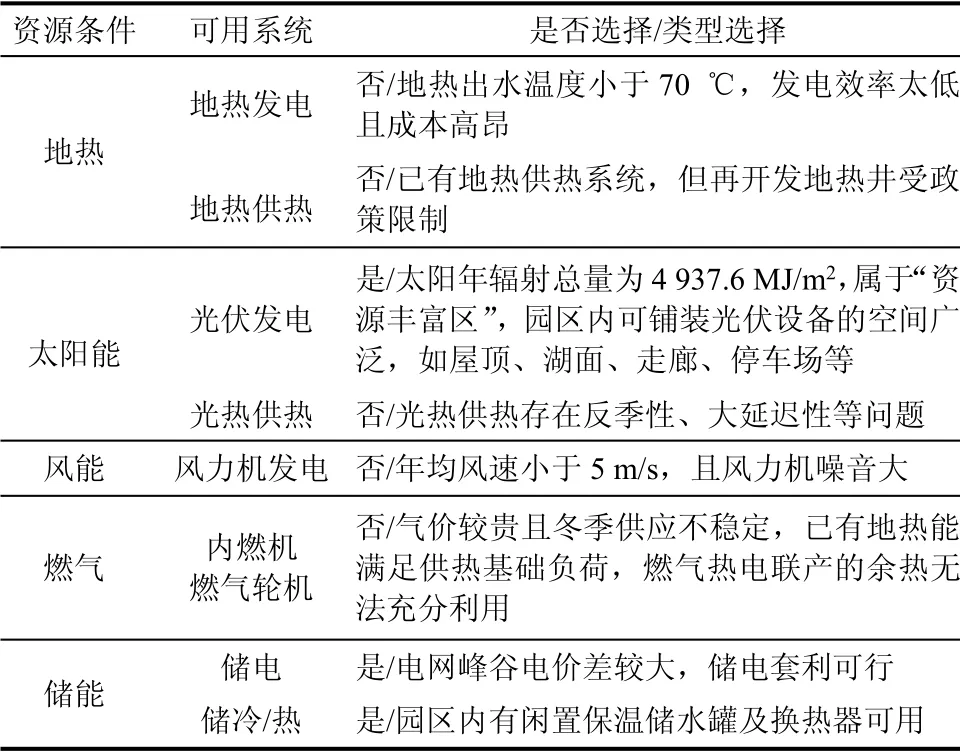
表1 可再生能源及储能类型选择Tab.1 The type selection for renewable energy and energy storage

表2 模型主要参数Tab.2 Main parameters of the model

多能互补系统运行方式如图3所示。其中，荷电（能）状态表示储能设备的剩余电（能）量与总容量之比。该区域对于光伏余电上网补贴政策不明朗，因此园区内光伏自发自用。由于每日有2 个电费高峰时段，为将峰谷电价差套利最大化，蓄电池每日2 次充电、2 次放电；在供暖和供冷季中，蓄水罐每日2 次储能、2 次释能。确定多能互补系统运行方式后，可根据2018年太阳能资源和园区实际负荷，逐时计算体现用能经济性的目标函数，并以2018年电费与目标函数之差作为粒子群算法的适应度函数。

图3 多能互补系统运行方式Fig.3 The operating mode of the multi-energy complementary system

应用粒子群算法优化参数有、光伏装机容量CPV(kW)、蓄电池储电容量CB(kW·h)、蓄水罐容量CW(kW·h)，因此粒子维度为4。将各个粒子带入计算适应度函数，而约束条件转化成为粒子更新位置的定义域限制。采用动态变化的惯性权重因子w更新粒子位置，取[wmin,wmax]=[0.3,1]，则采用动态变化和固定的w时适应度函数值（标幺后）进化曲线对比如图4所示。

图4 适应度函数值进化曲线Fig.4 The trend lines of fitness function

由图4可见，w动态变化的粒子群算法迭代8次后收敛至最优值，该最优值好于w取固定值时的计算结果。采用惯性权重因子动态变化的粒子群算法优化结果[β,CPV,CB,CW]=[0.13,0.25,405,650]时，多能互补系统经济性最佳，每年经济效益33.42 万元。

4 结 论

1）采用惯性权重因子动态变化的粒子群算法，将并网型多能互补系统规划的约束条件和目标函数分别转化为粒子群运动域范围和寻优的适应度函数，对多能互补系统的各类设备容量进行优化，使之满足系统经济效益最大化要求。

2）以某旅游度假园的多能互补系统规划为例，优化规划结果可使系统每年获益33.42 万元。

3）尽管本文提出的惯性权重因子动态变化的粒子群算法优化结果好于标准粒子群算法优化结果，但是算法仍存在陷入局部最优的风险，因此需要从理论上进一步证明优化结果的全局有效性。