基于灰色GM(1,1)改进模型的年度风功率预测

(华电电力科学研究院有限公司，杭州 310030)

0 引 言

年度风功率具有预测期间长，影响因素众多的特点，采用数理统计方法预测精度较低。灰色预测模型GM(1,1)所需要的负荷数据较少，而且不用考虑其分布规律，可应用于年度风功率预测。

但GM(1,1)模型也存在一些不足之处。一是原始数据灰度越大，预测精度越差；二是不适合于长期后推若干年的预测，有意义的仅仅是前一两个预测数据[1]。为此，文中从两个方面对GM(1,1)模型进行改进，一是对累加生成数列进行平移变换，二是对GM(1,1)模型中的背景值构造公式进行改进。并应用该改进模型对某风电场测风塔年平均风速进行预测，结果表明改进模型的预测精度有一定提高。

1 GM(1,1)的建模过程

GM(1,1)模型是应用非常广泛的一种灰色模型，它的建立只需要一个数列。具体步骤如下：

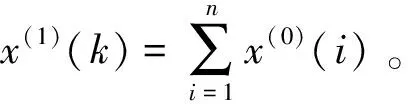
(1)

式中，a为发展系数，反应x(0)序列的增长速度，x(1)(k)为背景值。将式(1)以离散形式表示，并采用最小二乘法，可以得到a和u的估计值。

(2)

其中:

Y=[x(0)(2),x(0)(3),…,x(0)(n)]T

(3)

(4)

a和u的估计值确定后，可以确定微分方程式(1)，解微分方程并对其进行累减还原，得到x(0)预测方程：

k=(0,1,2…)

(5)

2 对GM(1,1)模型的改进

2.1 对累加生成序列进行平移变换

原始数据的离散程度较大时，预测误差比较大。针对这一问题，文中采用对累加生成序列进行平移变换的方法。将GM(1,1)模型中的背景值x(1)(k)换为x(1)(k)+w，然后建立优化模型，求得最佳的平移值w。

(k=2,3,…n)

(6)

从式(6)可以看出残差和平移值w的数量关系，为了得到残差值最小的平移值，建立如下目标函数：

(7)

通过对w求导并令其为0，可得最佳w值为：

(8)

2.2 改变微分方程的背景值构造公式

GM(1,1)模型的灰微分方程为：

x(0)(k)+az(1)(k)=u,k=2,3,…n

(9)

在原始模型中有：

z(1)(k+1)=0.5[x(1)(k)+x(1)(k+1)],

k=1,2,…n-1

(10)

式(10)是一个平滑公式，当时间间隔较短，原始数据变化幅度较小时，采用式(10)是合适的。然而，当原始数据变化幅度较大时，采用这样的背景值公式会使得预测误差很大。从z(1)(k)的几何意义出发，文中构造如下公式：

(m-1)x(1)(k+1)],k=1,2,…n-1

(11)

(12)

(13)

将该模型称之为GM(1,1,m)模型。

3 实例分析

选择某风电场测风塔2007～2014年年均风速(单位：m/s)为原始数据序列，利用MATLAB建模，预测2015～2018年年均风速。文中对原始GM(1,1)模型做了两项改进，为验证各项改进的单项效果和综合效果，做如下计算(2007～2014年原始数据及各序列拟合值见表1，各序列参数及后验差检验见表2，2015～2018年预测值及误差分析见表3)。

(1)令原始数据为序列0，不对其进行处理，采用原始GM(1,1)模型进行预测，得到数据序列1，并对其进行后验差检验和误差分析。

(2)利用公式(8)计算平移值，将累加生成序列平移变换，采用原始GM(1,1)模型进行预测，得到数据序列2，并对其进行后验差检验和误差分析。

(3)不对累加生成序列进行处理，采用GM(1,1,m)模型进行预测，得到数据序列3，并对其进行后验差检验和误差分析。

(4)对累加生成序列进行平移变换，同时采用GM(1,1,m)模型进行预测，得到数据序列4，并对其进行后验差检验和误差分析。

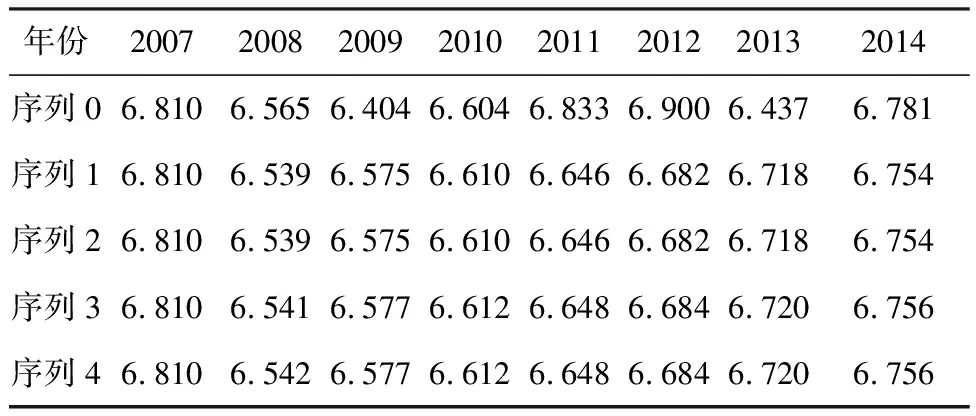
表1 2007～2014年各序列拟合值

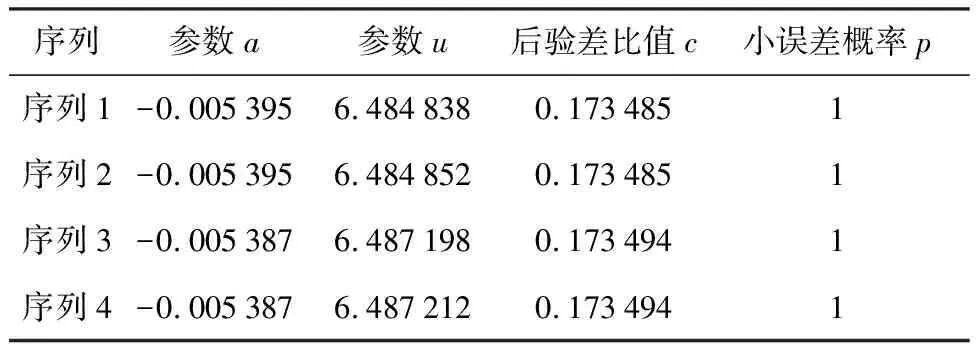
表2 各序列参数及后验差检验

由表2可知，各序列后验差比值均小于0.35，小误差概率均大于0.95，预测精度全部为一级。

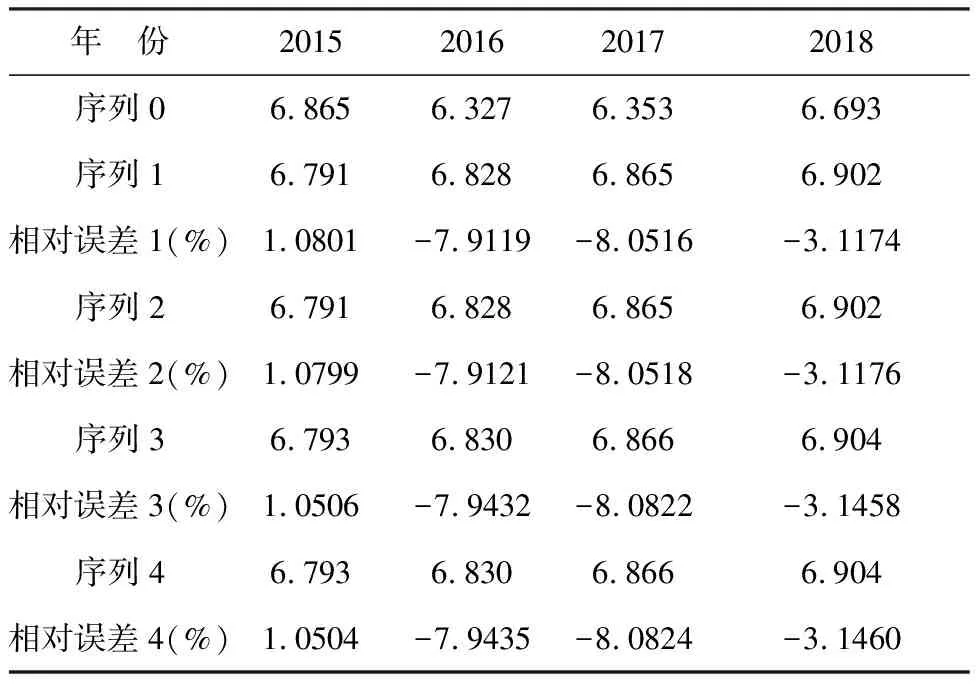
表3 2015至2018年各序列预测值及误差分析

分析表3中2015年和2016年的预测值及相对误差，将序列2、3、4和序列1对比可知，对累加生成序列进行平移变换和改进背景值构造公式，均可以提高预测精度，改进背景值构造公式对提高预测精度的贡献更大一些。

分析2017年和2018年预测值及相对误差可知，其预测精度变化不具有规律性。这也证明GM(1,1)不适合于长期后推若干年的预测，有意义的仅仅是前一两个预测数据。

4 结束语

文中针对原始GM(1,1)模型的不足之处，从两个方面对其进行改进：对累加生成序列进行平移变换，改善背景值构造公式。并应用改进模型对某风电场测风塔年均风速进行预测，预测结果表明其可行有效。