基于CTDEA算法的车辆+UAV配送路径优化

韩 明,王亚彬，丁连永，王添幸

(1.陆军工程大学石家庄校区，石家庄 050003；2.32653部队，沈阳 110163;3.国防大学联合作战学院，石家庄 050084)

维修保障主要以抢救抢修为主[1]，在未来信息化精确打击的对决下，武器装备维修器材需求随机性大、位置分散，这对配送的机动能力和时效性提出了更高要求。特别是中印边境高寒山地地区，主战场位于狭长通道，山高谷深、地形复杂；交通设施条件落后；冰冻、雪崩等多发恶劣天气易阻断投送路线；有效保障时间有限(下午4、5点至半夜持续风沙不能进行维修操作)；车辆性能下降(发动机功率下降30%，载重量下降25%)，故障高发；有生力量非战斗减损严重，单兵力竭运动易产生急性肾损伤、炎症反应和雪盲。这导致高原山地车辆行速度缓慢，行驶范围受限，基本依靠人力进行“最后一公里”的末端配送，严重制约我军维修器材的配送效率。

由Dantzig于1959年提出的车辆路径优化问题(Vehicle Routing Problem,VRP)是典型的NP难问题。其变体问题——带时间窗的车辆路径规划问题(Vehicle Routing Problem with Time Window,VRPTW)是当前物流领域研究的热点和难点。广泛学者主要围绕着该问题模型完善和求解算法改进进行了深入研究。如关于拥堵情形下的城市配送和互联网租车等一系列VRPTW模型的构建[2,3]，以及多agent蚁群算法，改进蝙蝠算法，改进遗传算法等VRPTW求解算法的设计[4-6]。但针对高原山地维修器材配送问题的VRPTW模型和算法成果较少。

针对上述问题，本文在前人研究的基础上[7]，提出了高原山地“车辆+无人机”这一半无人化配送模式，构建了对应的VPRTW模型，并根据问题特征应用CTDEA算法对该问题进行了求解。

1 “车辆+无人机”配送模式

车辆配送是指对一系列卸(装)货点，组织适当的行车线路，在一定约束条件下(如货物需求量、发货量、交货时间窗，车辆容量限制、时间限制等)的情况下，使车辆有序通过它们，以达到一定的目标(如距离最短，成本最低，时间最短等)。其特点是规模经济性，但其单位配送成本高，载货量较大，行驶范围较广但是受地形影响大[8,9]，如图1。

图1 车辆配送模式下的路径规划示意图

无人机是(Unmanned Aerial Vehicle，UAV)一种无需人员驾驶的空中飞行器，其利用内部配置的无线电遥控设备和预先编制好地控制程序实现自主飞行、独立完成作战或保障任务[10]。UAV具有机动灵活，隐蔽高效，安全经济，受天气、地形、道路交通影响小(见图2)[11]，但载重量有限，飞行半径较小的特点，见表1所示。

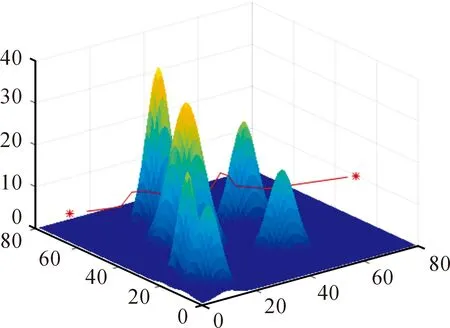
图2 车辆不可通行地域的UAV配送示意图

表1 UAV特点性能

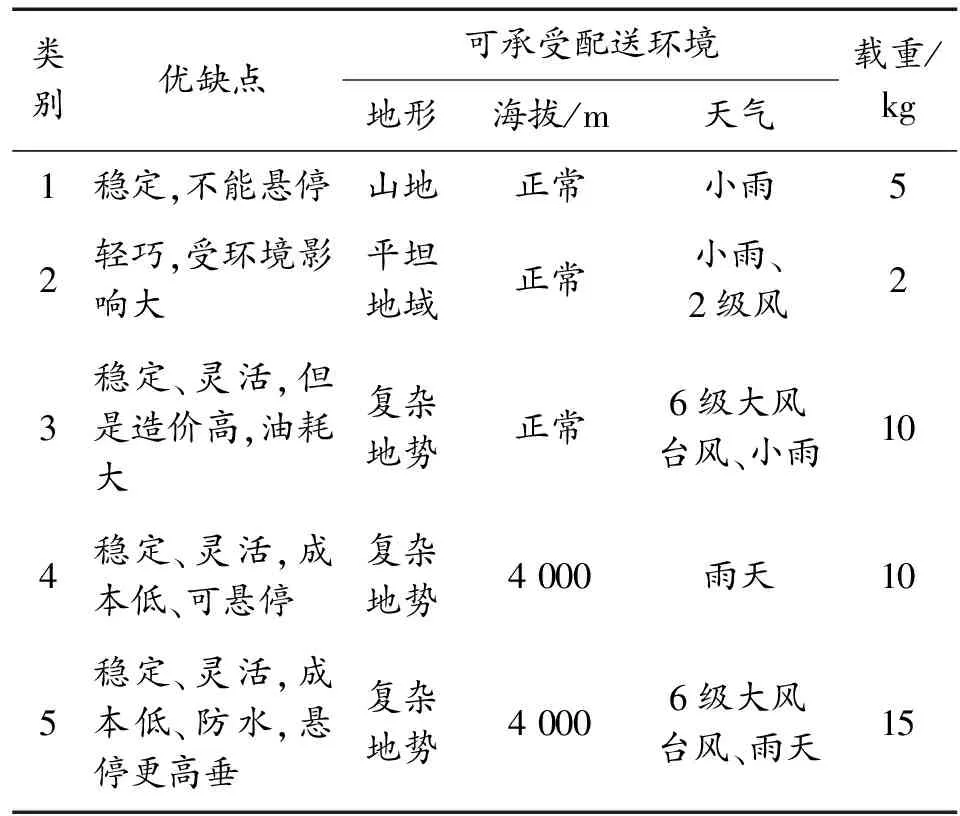
类别优缺点可承受配送环境地形海拔/m天气载重/kg1稳定,不能悬停山地正常小雨52轻巧,受环境影响大平坦地域正常小雨、2级风23稳定、灵活,但是造价高,油耗大复杂地势正常6级大风台风、小雨104稳定、灵活,成本低、可悬停复杂地势4 000雨天105稳定、灵活,成本低、防水,悬停更高垂复杂地势4 0006级大风台风、雨天15

注意：1为固定翼UAV，2为无尾翼UAV,3为无人直升机,4为四旋翼UAV,5为六旋翼UAV。

UAV配送模式在军用和民用领域取得了长足发展。早在阿富汗战争，美军无人运输机K-MAX就出色完成了从后勤基地到偏远山区前线阵地的配送任务，标志着UAV以“空中挑夫”身份正式出现在战时配送领域。当前，军用UAV配送了切合未来战争的信息化、网络化、无人化的需求。在民用领域，UAV配送技术迅速风靡国内外。在国外，Reykjavik实现UAV送货上门；ZIPLINE公司实现UAV以高达100 km/h的时速向诊所运送血液。在国内，顺丰建立了大型物流UAV基地，并提出“大型有人运输机+支线大型UAV+末端小型UAV”的三段式空运网实现36 h通达全国的设想；京东研发出了能够全自动化配送货的六旋翼UAV；饿了么，美团外卖获准开辟UAV即时配送航线，实现了UAV外卖配送的合法化,大幅提高了配送效率。

高原山地维修器材需求呈群落分布，群内需求量小、时效性强、位置分散且多位于车辆不可通行地域。传统“车辆+人力”配送模式效率不高的问题亟待解决。当前UAV性能已可以胜任恶劣天气下的高原山地配送任务(见表1)。车辆与UAV配送特点如表2，本研究通过UAV与车辆的优势互补，用UAV取代传统人力搬运作为直达作战单元的配送方式，提出了一种“车辆+UAV”的高原山地维修器材配送模式。

表2 车辆与UAV配送特点

该模式的具体配送过程如下：配送中心对所获取的作战单元的需求利用诸如细菌搜索算法(Bacterial Foraging Algorithm,BFA)、K-means等聚类算法，对需求进行预处理，然后通过任务匹配确定执行任务的仓库。按照车辆通行良好地域由车辆进行配送，车辆通行受限地域由车载UAV进行配送的原则，进行配送路径规划以实现总配送时间最短，如图3所示。

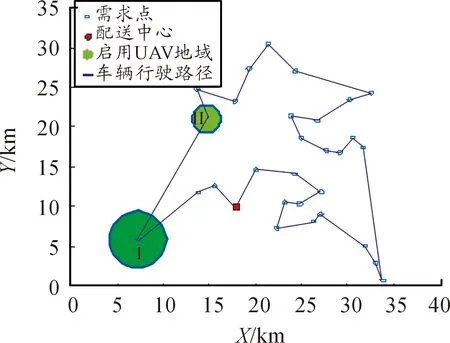
图3 车辆+UAV配送路径宏观示意图

“车辆+UAV”配送模式在配送过程中3种运动形式：① 同时启用车辆和无人机均处于动态配送；② 受通行范围限制，车辆在某一集散点等待，启用无人机赴附近作战单元进行配送，配送完后返回车辆所在位置；③ 车辆通行条件良好，启用车辆配送，无人机暂不启用。如图4所示，此处考虑高原山地配送实务的特点，对如图4(b)所示的情形进行研究。

2 车辆+UAV配送模式的模型设计

本文研究图4(b)下的“车辆+UAV”路径问题，可以看成嵌套的两级带时间窗的车辆路径规划(Vehicle Routing Problem with Time Windows,VRPTW)问题，车辆路径规划为Ι级VRPTW问题，UAV配送为ΙΙ级(即Ι级问题的子级问题)VRPTW问题。建模思路为，首先按车辆通行情况和距离对提出维修器材需求的作战单元进行聚类分析，处理为作战单元需求群，将每个需求群组视为1个Ι级需求点对车辆路径进行优化。车辆通行受限的需求点，由车辆进行配送，车辆通行范围受限需求群组启用车辆+UAV配送模式，由车辆行驶至集散点，由无人机进行配送，其实质为一个局部VRPTW问题。故，车辆与UAV均遵循以下模型。

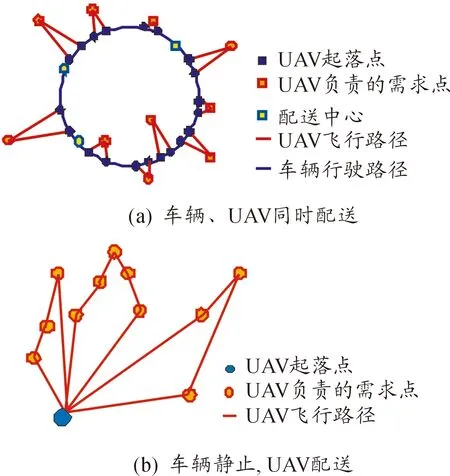
图4 车辆+UAV配送路径局部示意图

2.1 符号说明

f(x):军事效能；E：军事效益

C1：电耗成本；C2：时间成本；C3：惩罚成本

w1w1,w2,w31：C1,C2,C3所对应的权重

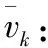
θ1：运输工具空载时单位距离耗油/电成本

θ2：运输工具满载时单位距离耗油/电成本

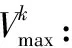
qg：需求点的需求量

cfk：每动用每一运输工具的固定成本

Rk：所启用的每一运输工具数量

[ETi,LTi]：作战单元的时间窗

M1(ti)：早到的惩罚成本函数

M2(ti)：[ETi,LTi]内到的惩罚成本函数

M3(ti)：晚到的惩罚成本函数

Vj：需求器材的容积；bj：需求器材的尺寸

2.2 模型构建

(1)

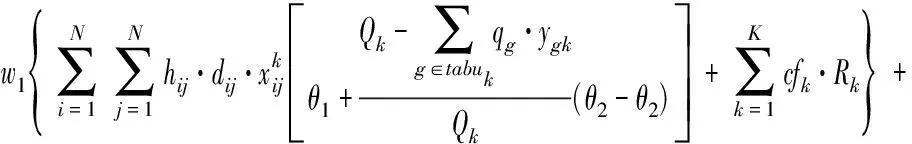
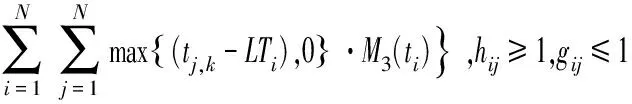
(2)

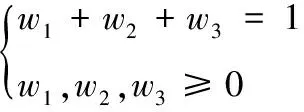
(3)

(4)

(5)

(6)

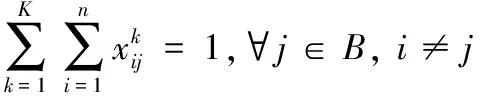
(7)

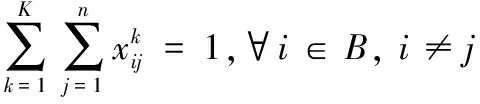
(8)

(9)

twait,i,k=max(ETi,k-ti,k,0)

(10)

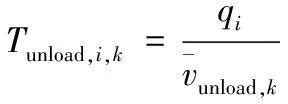
(11)

tj,k=ti,k+twait,i,k+Tunload,i,k+tij,i,k

(12)

(13)

(14)

(15)

根据高原山地军用维修器材配送任务的特点，本研究将军事效能最大化作为目标函数，见式(1)。由于指定配送任务对应的军事效益E为定值，所以上述目标即可转化为油/电耗成本、时间成本和惩罚成本最小化，见式(2)。结合高原山地配送中道路弯多坡陡，车辆故障高发，车速受路况影响较大，且油耗成本大的实际，引入了距离修正因子hij和速度修正因子gij和基于车辆实载率核算的单位油耗成本(对于不受上述因素影响的UAV，其对应参数hij,gij可取1)。上述模型中的hij,gij可由信息平台根据所获取各节点间路段i→j的实时道路信息进行赋值，θ1,θ2根据信息平台记录的车辆油耗历史数据得到。由于实际情况下作战单元的时间窗为无时间窗、软时间窗、硬时间窗、混合时间窗共存，故本文通过设置不同时段的惩罚函数来描绘不同时间窗下的惩罚成本。其中，无时间窗情况下，M(ti)均取0；硬时间窗下，令M1(ti),M3(ti)→∞，M2(ti)取1；软时间窗和混时间窗下根据作战单元需求规律设置惩罚函数表达式。式(3)表示多目标处理为单一目标函数时各子目标的权重约束。由于维修器材装载不同传统物资装载，所以其装载除了车辆载荷和容量约束外，还要考虑装货尺寸的约束，见式(4)～式(6)。式(7)～式(9)分别表示每个作战单元最多有且只有一辆运输工具为其服务;运输工具访问每个节点后必须从该节点驶离，然后进行下一个作战单元的配送或返回配送中转点(起始点)；运输工具必须从起始点出发最终返回起始点，并且运输工具数量不能超过可用运输工具总数K。式(10)～式(12)分别表示在作战单元处i的等待时间，卸货时间和到达作战单元处j的时间，其中卸货时间由器材卸货量和器材的卸货速度决定。式(13)～式(15)均为0-1决策变量。

3 求解算法

无人机配送路径规划问题的实质仍为VRPTW问题，二者均属于NP-hard问题，一般采用启发式算法来进行求解。以GA算法为代表的进化算法因具有较高的鲁棒性、高效率和广泛适用性的全局优化特点，被广泛用于上述大规模复杂组合优化的求解。但是传统演化算法普遍存在由于种群多样性下降而导致过早收敛，陷入局部最优的局限。针对这一问题，谭阳等[12]提出了基于染色体异位的动态进化算法(Chromosomal Translocation-based Dynamic Evolutionary Algorithm,CTDEA)，该算法在维护种群多样性、求解速度、解的精度、和稳定性上较遗传算法(GA)均由明显改进。故此处选取该算法对上述VRPTW+UAVRPTW问题进行求解。

3.1 算法步骤

步骤1 初始化种群P0;

步骤2 互斥操作：对Pt进行互斥操作(去除差个体i,j间差异度d(ai,aj)相同的个体)并根据目标适应度Fit(f(ai))按降序排列。

(16)

其中，Div(ai)为个体在种群中的差异度。

步骤3 判断是否满足终止条件，满足即跳出循环，否则继续执行步骤4。

步骤4 精英策略：筛选Fit(f(ai))排序为前m的个体构成精英群，并计算Div(ai)

步骤5 交叉操作：其余n-m个体，根据式(17)在步骤4的精英群中选择一个精英个体，按式(18)进行交叉操作

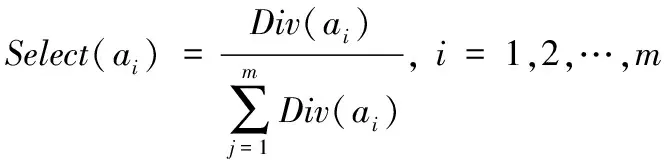
(17)

(18)

其中，ai,l表示个体ai在其种群中的第l个编码位。

步骤6 多样性度量。计算当前基因矩阵所有列的多样性度量Div(j)，将结果按降序排列存入Div_column，按式(19)求基因矩阵多样性度量Div(At)；

(19)

其中，Div(At)=0,1,2,…,n×L,且其值越逼近0，种群多样性越高。

步骤7 易位操作：根据式(20)对比多样性Div(At)，根据K值，按式(21)对Div_column中的前K列进行反置易位操作，之后执行步骤2。

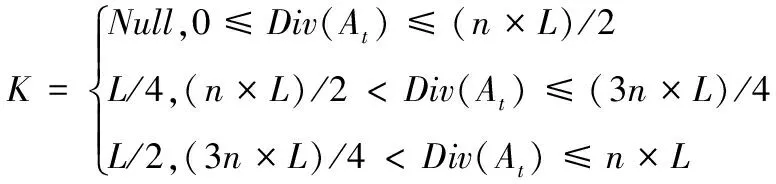
(20)

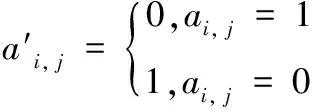
(21)

3.2 算法流程

CTDEA算法流程如图5所示。

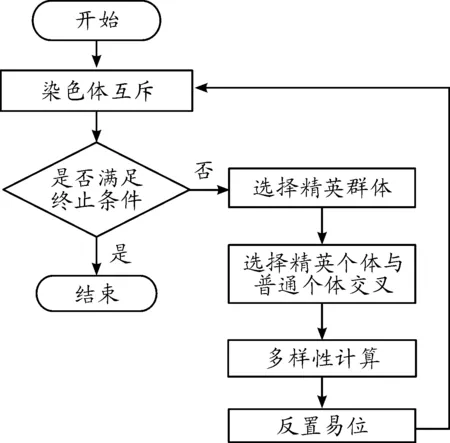
图5 CTDEA算法流程框图

4 算例分析

4.1 背景案例

假设配送中心收到高原山地作战单元维修器材需求信息见表3。

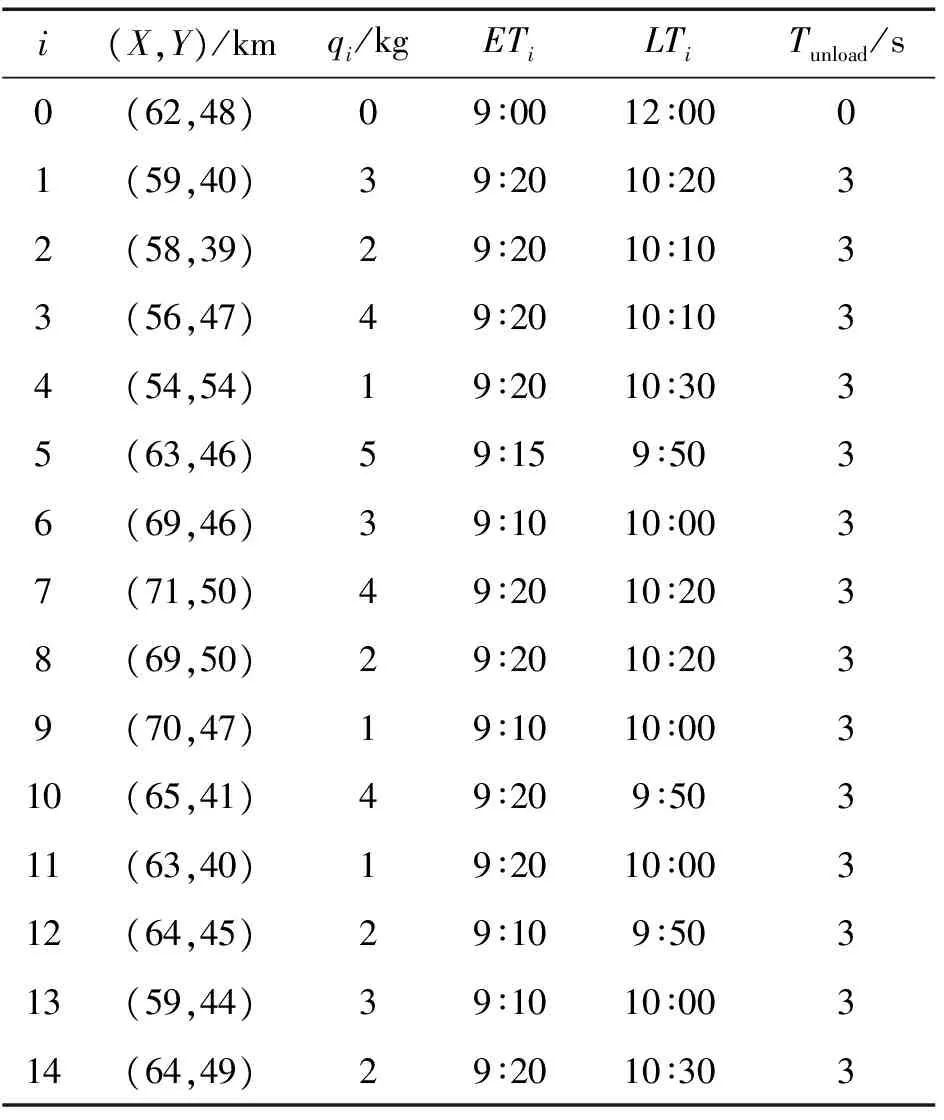
表3 作战单元需求信息

经过任务匹配，仓库A负责此次配送任务。考虑由于该次配送任务所属地域地形复杂，车辆通行范围受限，故调用车辆+六旋翼UVA执行此次任务,该UAV性能见表1，飞行半径20 km，平均航行速度为15 m/s。配送流程为车辆装载UVA直达中转集散点0，然后启用UAV进行“最后一公里”末端配送。车辆至0的路程为20 km,平均车速为60 km/h，最载重1.6 t，该车队于9点从A出发。要求对UAV配送路径进行规划，使得在动用UAV架次最少的基础上实现配送时间最短。

4.2 CTDEA算法和GA算法运行结果

由于车辆均是从A到0，距离均为20 km，用时20 min,抵达中转点0的时刻为9∶20≤ETi,故该背景案例中的VRPTW+UAVRPTW问题，仅需要对UAVRPTW进行处理即可。利用CTDEA算法和GA算法同时求解，Matlab的运行结果如表4、表5所示。

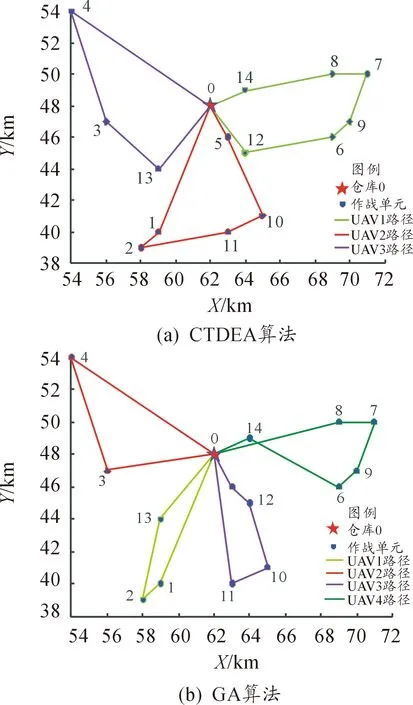
图6 CTDEA算法和GA算法下的UAV配送路径图

表4 CTDEA算法求解结果

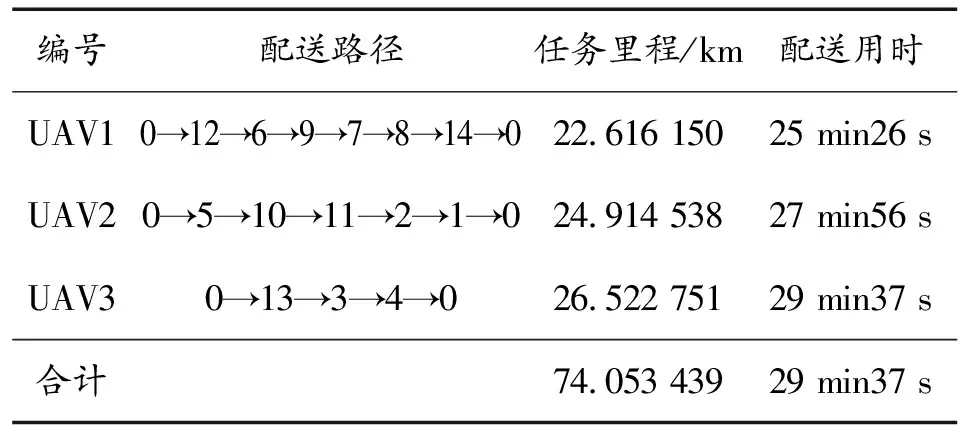
编号配送路径任务里程/km配送用时UAV10→12→6→9→7→8→14→022.616 15025 min26 sUAV20→5→10→11→2→1→024.914 53827 min56 sUAV30→13→3→4→026.522 75129 min37 s合计74.053 43929 min37 s

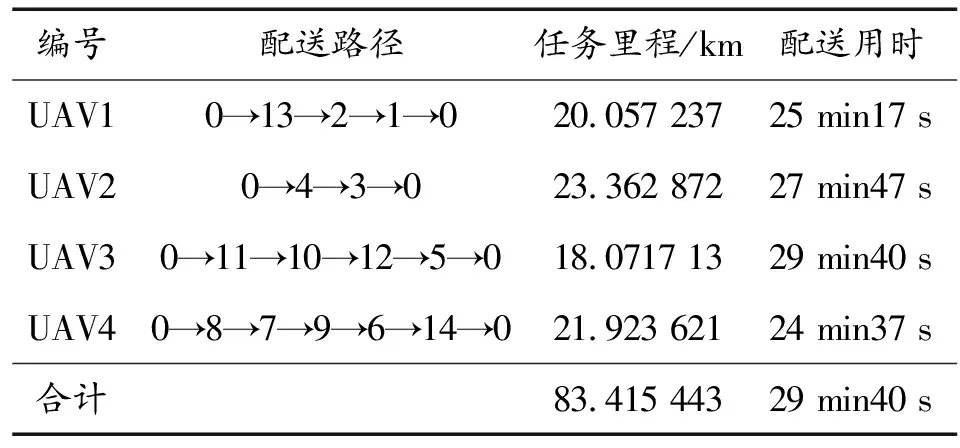
表5 GA算法求解结果

如表4、表5所示，CTDEA算法求解结果为UAV动用架次为3，总任务里程为74.053 4 km，由于UAV并行执行任务，总任务耗时29 min37 s，GA算法求解结果为UAV动用架次为4，总任务里程为83.415 4 km，总任务耗时29 min40 s,如图6所示。

通过对高原山地维修器材配送实际的背景案例的仿真分析，发现CTDEA算法在求解质量和收敛代数方面均好于GA算法(见图7)，有效解决了传统进化算法因种群多样性下降导致早熟问题。其中，GA算法在进入较少代数后由于受目标函数极小值吸引速丧失种群多样性，陷入局部最优，全局搜索能力较差。相比于GA算法，CTDEA算法能够通过染色体异位保障了种群多样性，从而使得算法可以跳出陷入局部最优的困境，避免算法过早进入早熟，提高了算法的全局搜索能力和求解质量；同时从收敛代数上来看，CTDEA算法具有较好局部寻优能力和收敛速度。

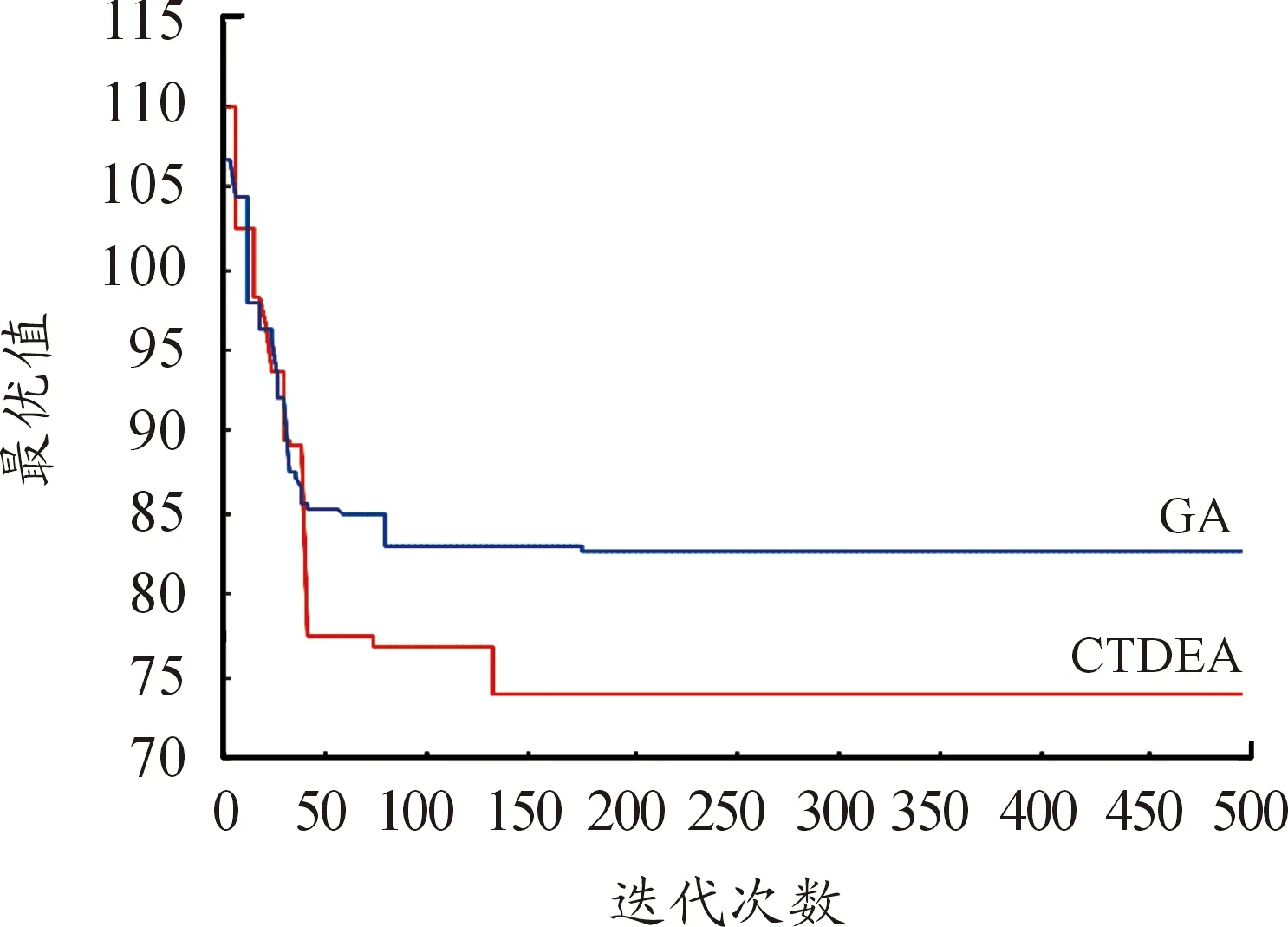
图7 CTDEA算法与GA算法下迭代次数与最优值关系

4.3 “车辆+UAV”和“车辆+人力搬运”

根据高原山地单兵负重研究，海拔3 700 m人力搬运速度为4 km/h,4.5 km/h,5 km/h分别对应基准适宜负重为20.5 kg,18.0 kg,15.0 kg。鉴于配送任务的时效性，选取5 km/h,15.0 kg这一数组用于对比，Tunload取1 min/单元。通过求解，得该模式需3名单兵，总里程74.053 4 km，合计用时5 h21 min,配送效率为“车辆+UAV”的1/10.84，且难以满足时间窗需求。

5 结论

本文提出了一种“车辆+UAV”的半自主配送模式。通过仿真实验验证了“车辆+UAV”配送方式较传统配送方式在配送效率和时效性方面的优越性以及CTDEA算法的有效性。