基于PSO-GA混合算法的末端防御兵力优化部署方法

温包谦，王 涛，成 坤，张济众

(1.火箭军工程大学，西安 710025；2.火箭军装备部，北京 100085)

兵力优化部署是指在满足一定约束条件下，合理部署各型防空武器于防御区域，使得防空武器系统的综合防御效能最大[1-2]。以往的防空作战中，将远程、中程、近程防空武器优化部署于要地周围，有序拦截空袭编队预警机、轰炸机群，载机投放的导弹、炸弹等目标。但随着现代科技的发展，敌方采用灵活多样的空袭武器和作战样式来低空突袭我方要地，使得重要目标面临严重威胁，因而要地的末端防御是未来防空作战亟待解决的重要课题之一。

近年来国内学者对于要地防空兵力优化部署问题做了很多研究。文献[3]利用Memetic算法进行要地防空兵力部署，但没有考虑火力单元离要地中心配置距离对部署方案的影响。文献[4]在火力单元数量一定的条件下，寻找一种合理有效的部署方案，但没有考虑火力层数对部署方案防御效能的影响，使得最终的结果并不是很理想。文献[5]运用粒子群算法求解区域防空优化部署的数学模型，但由于PSO算法容易早熟，因此所得的结果并不精确。

针对目前要地防空兵力优化部署研究的不足，本文在求出要地基本部署方案所需兵力总数的条件下，描述了基于火力覆盖能力的部署方案优化目标，并将火力单元离要地中心配置距离和火力层数作为约束，建立了要地防空兵力优化部署模型，并构造了PSO-GA混合算法优化求解。仿真实验验证了所提优化模型和算法的有效性和合理性。

1 问题的数学描述

1.1 备选位置确定

实际的防区是连续分布的，理论上只要满足部署约束条件的任何位置都可以成为火力单元的备选部署位置。但是如果要进行定量的优化计算，就必须先将备选部署位置进行量化处理[4]。

利用文献[6]中提出的环形网格化思想对要地进行离散化，如图1所示，将网格的交叉点作为可部署位置，并可以作为评价火力覆盖效果的采样点。网格大小应根据防区部署需求合理设置，网格越密集，可部署位置越多，计算量会增加，同时也提高了解的质量。

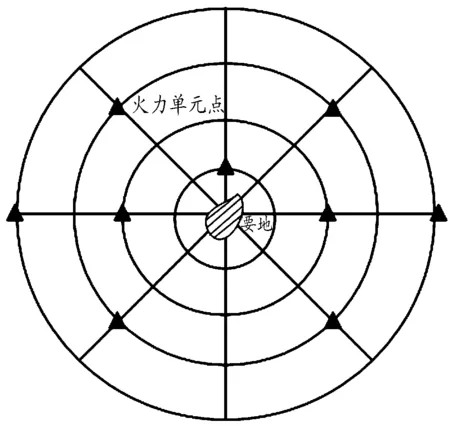
图1 防区网格示意图

1.2 确定所需兵力总数

阵地部署形式指的是火力单元在部署空间呈现的形式。目前，公认的阵地部署形式一般分为四种：环形部署、扇形部署、线形部署、集团部署[7]。本文研究的优化部署问题是指：在求出环形部署所需总兵力的基础上，寻找一种合理有效的部署方案，使得对重点保护对象和目标主要来袭方向的防御能力最大。

环形部署所需兵力总数的计算公式为[8]：

(1)

式(1)中：2φmax为武器系统的掩护角；khl为武器系统的火力密度系数；[ ]为取整符号。

1.3 基本假设

1)我方有N套相同末端防御武器系统，敌机在杀伤区飞行的时间与系统射击目标所需时间大致相等，射击时间Tshot；

2)敌机总数是M架，进入防区的目标流视为泊松流，空袭时平均强度为λ架/min，突防目标也视为泊松流；

3)每个目标只分配给一个末端防御武器系统[9]；

4)要地防空中，来袭目标具有明确的攻击位置或有限的攻击范围。

1.4 约束条件的数学描述

现代空袭环境变得越来越复杂，空袭强度大，来袭方向具有随机性。对于末端防御武器系统保卫要地而言，为保证一定的火力纵深，需部署多道火力防线。从敌空袭角度考虑，各道火力防线上火力单元个数对于来袭目标的拦截概率是不同的，所以，确定火力防线个数对于火力单元优化部署是十分有必要的。本文为了简化问题研究，只考虑了两道火力防线，约束条件也是在此条件下进行描述的。

1.4.1火力单元离要地中心距离约束

就要地末端防御来说，火力单元离要地越远，火力单元对要地构成的掩护角越小，所需兵力越多。而且，对于多道火力防线部署，各道防线离保卫要地的距离不同，火力单元对于要地的防御能力也是不同的。因而，一个适当的距离，对于提高有限火力单元数量防御要地能力也是很重要的。

用dxi(i=1,2)表示该型防空武器与要地中心的距离，i表示火力层数，则须满足约束条件为：

Dn1≤dxi≤Dn2

(2)

式(2)中：Dn1是该型防空武器与要地中心的最小距离，由该型防空武器战术技术指标确定；Dn2是被防护要地的最大半径。

1.4.2兵力数量约束

用c1表示第一道防线上火力单元个数，c2表示第二道防线上火力单元个数，则须满足约束条件为：

c1+c2=Nh

(3)

式(3)中，Nh是防御来袭目标所需的总兵力。

1.4.3武器性能约束

αj表示任意两部防空武器之间的角度间隔，由该型防空武器战术技术指标确定，则部署火力单元j时，须满足60°≤αj≤120°。

1.5 火力覆盖能力的数学描述

在火力单元优化部署时，需要精确的指标来描述不同部署方案对来袭目标的毁歼能力。根据防空武器杀伤区几何特点和火力单元的迎头射击规律，防空武器在空袭兵器飞行高度的杀伤区截面近似为半圆形，且半圆直径垂直于来袭方向。如图2所示。

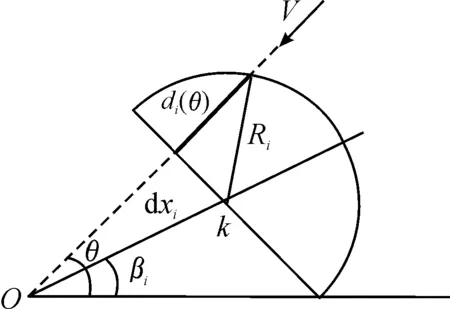
图2 防空火力拦截示意图

假设被保护对象位于O点，火力单元i位于k点，火力单元i相对要地的角度为βi，距离要地中心为dxi，火力半径为Ri，当目标沿θ方向以速度V来袭，目标在杀伤区的航迹长度为di(θ)，在该段被服务时间为tfi，被火力单元i拦截了ki(θ)次，每次拦截对目标的毁歼概率为pi，则火力单元i在di(θ)段对目标总的毁歼概率为：

pi(θ)=1-(1-pi)Ki(θ)

(4)

根据排队论的原理，当目标以θ方向来袭时，我方防空武器系统成功保卫要地的总毁歼概率p(θ)为：

(5)

1.6 数学模型

根据上述对火力覆盖能力和约束条件的定量描述，得到要地末端防御兵力优化部署的数学模型为：

(6)

数学模型的建立，将要地末端防御兵力优化部署问题转化为约束条件下的优化与决策问题。由于战场环境多变，候选部署阵地的增多、约束条件复杂，会出现组合爆炸，可行解的数量急剧增多，需要借助智能优化算法求解。

2 PSO-GA混合算法

2.1 粒子群算法(PSO)

PSO算法模拟鸟类觅食和人类的认知，是一种基于群体随机优化原则的算法[10]。每个粒子具有记忆能力，可以改变自身的位置和速度，从而向全局最优解靠拢。算法思想简单，易于实现并且收敛速度快，但容易陷入局部最优出现早熟现象，种群多样性差，搜索的范围小。

2.2 遗传算法(GA)

GA算法是一种模拟自然界生物进化机制的算法，遵循“适者生存、优胜劣汰”的法则[11]。算法经过遗传操作，产生出多样的解集种群，而且，迭代次数越多，种群数量越大，就越靠近最优解，适用于全局搜索，但个体没有记忆，遗传操作盲目无方向，收敛速度较慢，所以收敛时间长。

2.3 新的基于PSO和GA的混合算法

本文构造了一种基于PSO和GA的混合算法，先用PSO产生最优解的个体，再通过GA的选择、交叉、变异操作寻找最优解。充分利用GA算法的种群多样、随机全局搜索能力和PSO算法的个体记忆、收敛速度快等特性进行优势互补，来提高算法的搜索效率，增强算法的求解能力。

2.4 PSO-GA算法在防空兵力优化部署中的应用

用二进制0-1编码表示解，解的长度为备选部署点的数量，解的每一位字符代表了该点是否部署防空火力单元，解中“1”的个数即为防空兵力数量。

寻找最优解的过程中，初始种群pi根据如下的公式来更新自己的速度和位置，即：

(7)

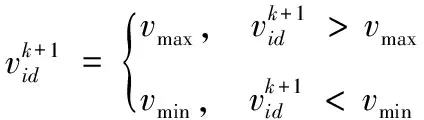
(8)

(9)

式(7)～(9)中，xid为位置矢量；vid为速度矢量；k为迭代次数；w为权重系数；c1和c2为学习因子；r1和r2为[0，1]范围内的均匀随机数。

1)选择算子

本文采用轮盘赌随机选择种群中的个体，保证个体被选择的公平性，遵循了遗传算法交叉变异随机性的原则。

2)交叉操作

在遗传进化过程中，交叉概率pc影响新个体的收敛速度，pc越大，新个体产生的速度越快，但是pc过大又会破坏高适应度个体的结构，因而采用一种自适应交叉概率方法[12]。

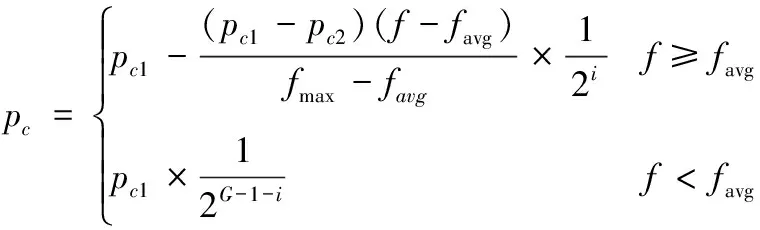
(10)

式(10)中:fmax为群体中最大适应值；favg为群体平均适应值；f为要交叉的两个个体中较大的适应值；pc1=0.9，pc2=0.6；i为迭代次数；G为基因链长度。

3)变异操作

对于变异概率pm来说，如果pm过大，那么遗传算法就变成了纯粹的随机搜索算法；如果pm过小，就不易产生新的个体结构，因此，变异算子也采用自适应变异概率的方法。

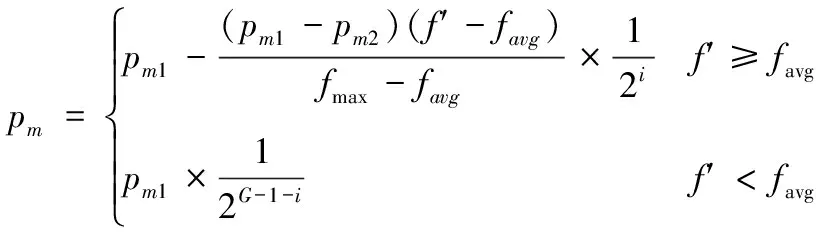
(11)

式(11)中:f′为要变异个体的适应度值；pm1=0.1，pm2=0.01，其他参数同上。

4)保留精英策略

为避免已经出现的好方案在遗传过程中消失，采取了保留精英策略。如果下一代群体的最佳个体适应值小于当前群体最佳个体的适应值，则将当前群体最佳个体或者适应值大于下一代最佳个体适应值的多个个体直接复制到下一代，随机替代或替代最差的下一代群体中的相应数量个体。

PSO-GA混合算法迭代流程框图见图3。

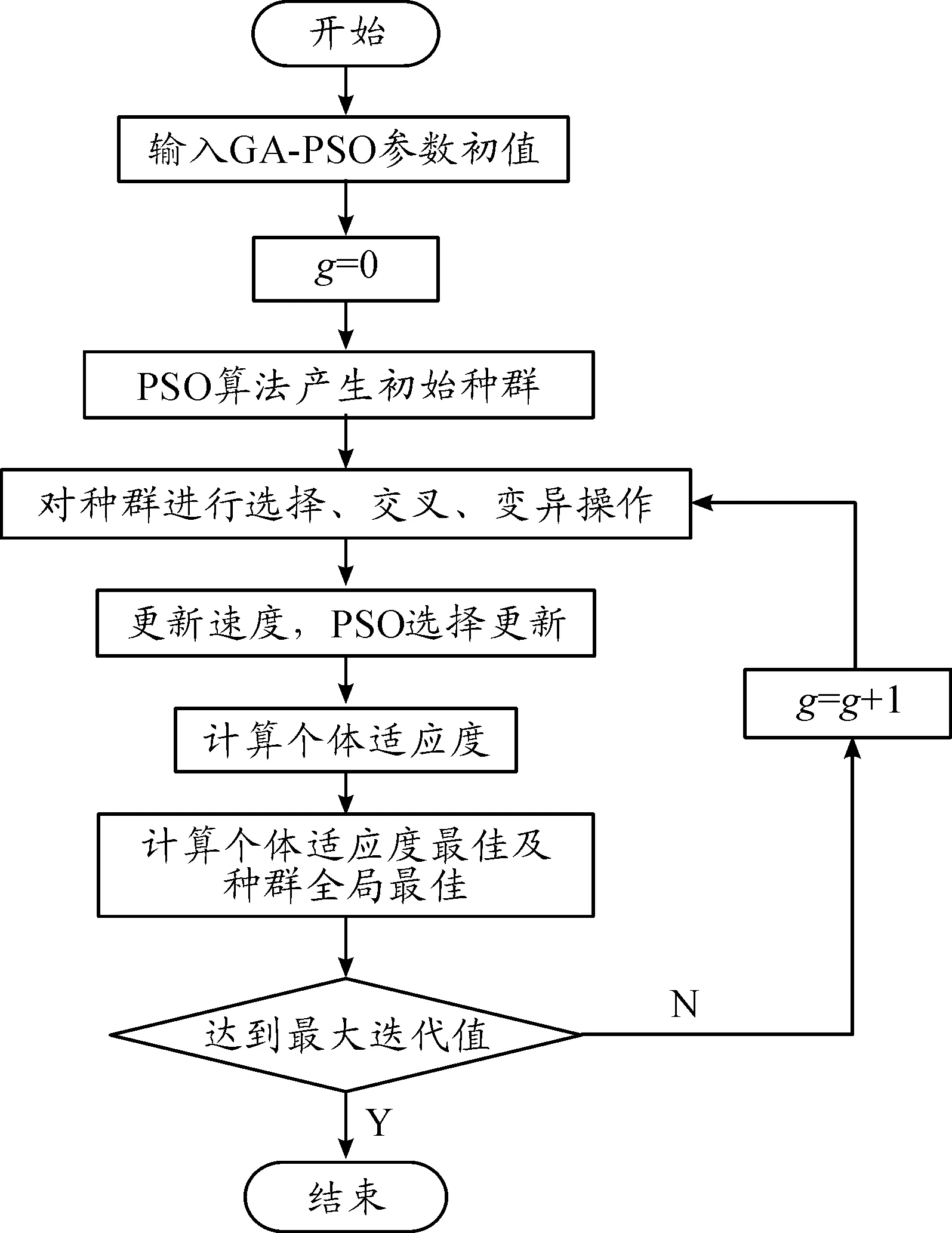
图3 PSO-GA混合算法迭代流程框图

3 实验与分析

首先利用无人机对需要部署该型号防空武器的环境进行野外实地测量，然后基于无人机航测数据，利用ArcGIS划定被保护对象和防区。假设用GIS选择出的部署要地是连续的，任意一点都可以部署火力单元。

在典型军事想定下进行火力单元部署，设需要被防护的要地半径20 km，将要地划分为6×20的环形网格，敌空袭武器载机飞行速度为400 m/s，最大航路角90°。其他参数如表1所示。

表1 防空武器参数

根据式(1)，求得要地防空环形部署时所需火力单元总数为6个。

仿真实验1

将6个该型号火力单元以单环形部署形式，均匀配置在离要地中心20 km的圆周上，由式(5)计算得到，此时火力覆盖能力为0.402。因此，需要按照上述提出的方法对火力单元进行优化部署。

仿真实验2

按照上述基于PSO-GA算法的要地防空兵力优化部署方法，解得两道防线上火力单元个数c1=4，c2=2；dx1=12 km，dx2=19 km，采用外层防线扇形部署，内层防线环形部署的部署方案，此时火力覆盖能力最大为0.85。

对比图4(a)和图4(b)易知，PSO-GA混合算法的适应度曲线在迭代次数约60时趋于平稳，迭代次数为60～200时没有出现较大变化，说明收敛较快。并且通过观察纵坐标，可以看出PSO-GA混合算法可以提高解收敛精度。

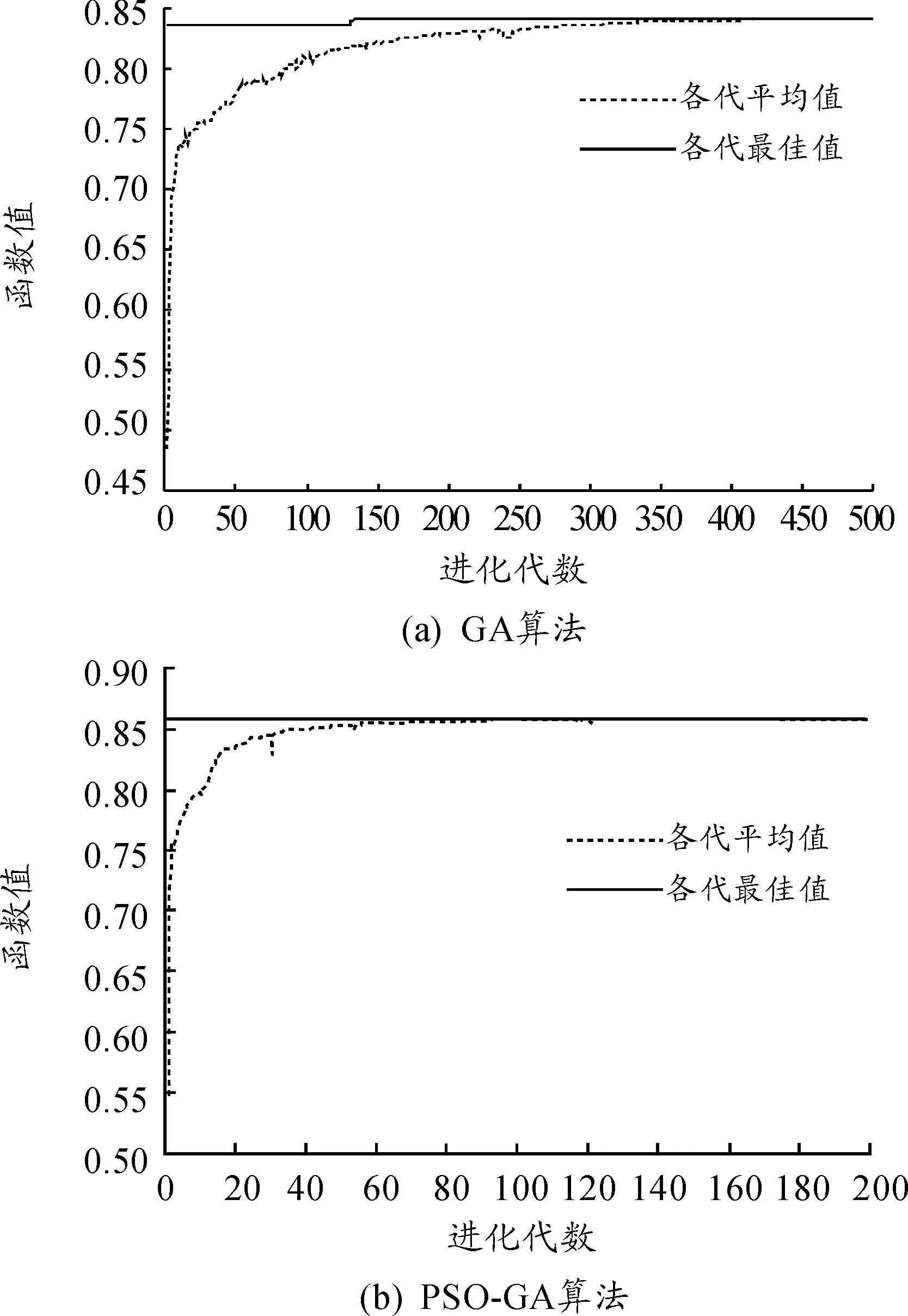
图4 算法最优适应度曲线

仿真实验3

为进一步说明扇形和环形配置顺序对火力覆盖能力的影响，将c1=4的火力层部署在离要地中心dx1=19 km圆周上，c2=2的火力层部署在离要地中心dx2=12 km圆周上，火力单元之间间隔部署，即内层防线扇形部署，外层防线环形部署，此时火力覆盖能力为0.44。PSO-GA算法最优适应度曲线如图5所示。

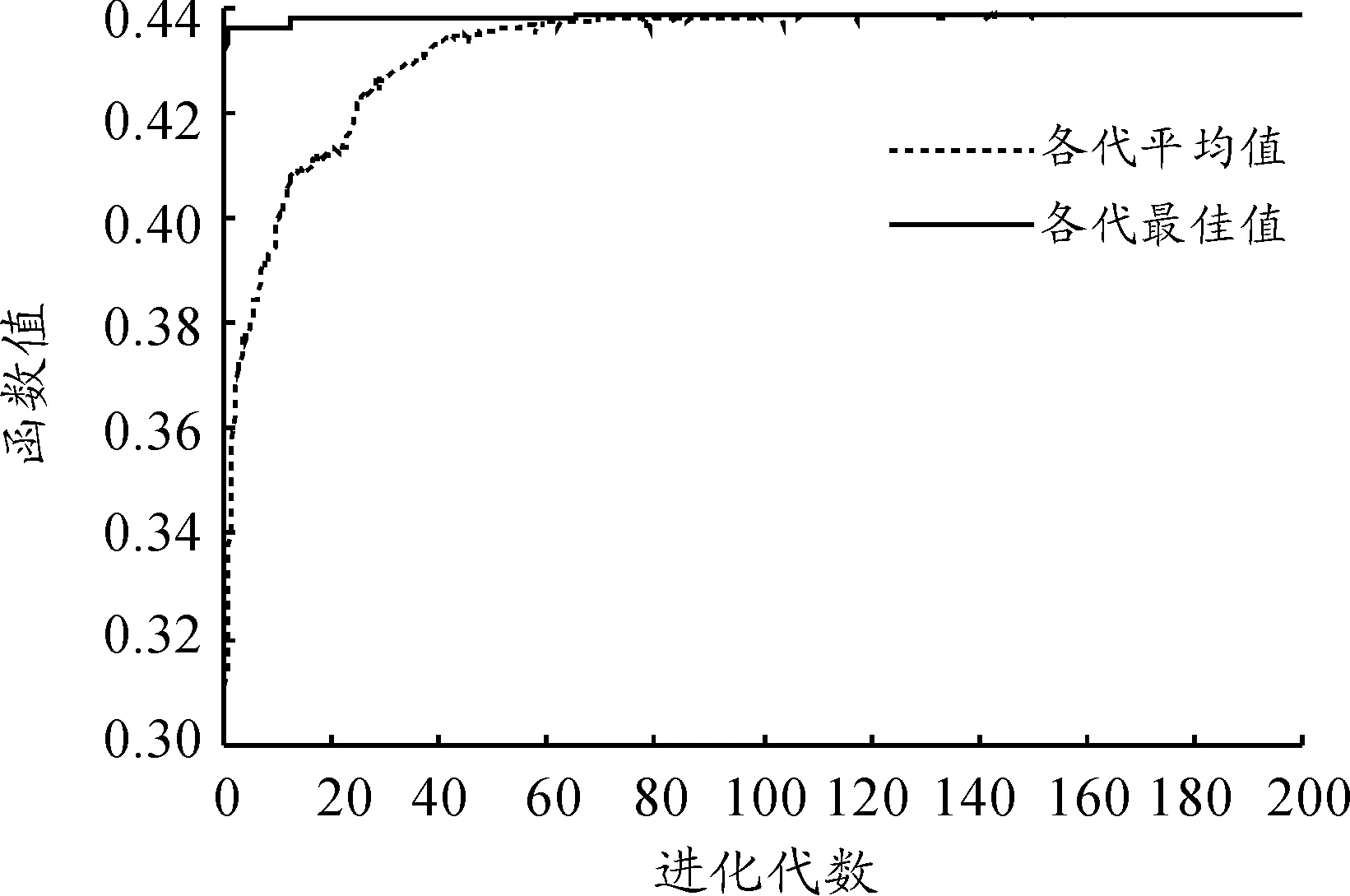
图5 PSO-GA算法最优适应度曲线

4 结论

1)实验结果表明，本文提出的兵力部署数学模型和PSO-GA混合算法可以有效结合能很好地解决网格化防空火力单元的优化布阵问题。

2)PSO-GA混合算法快速准确地从接近最优个体的种群中找到最优值，避免算法陷入局部最优值。

3)要地防空火力单元部署时，扇形部署和环形部署搭配使用火力防御效果明显优于单环形部署；外圈防御区在可能的主要作战方向采用扇形部署，内圈防御区采用环形部署是一种最优的部署方案。