金属丝杨氏模量实验的数据处理

高院丽

【摘 要】楊氏模量是描述固体材料抵抗外力产生拉伸或压缩形变能力的物理量[1]。测定材料的杨氏模量在工程技术实践中具有重大作用。本文介绍了拉伸法测量铁丝的杨氏模量。用逐差法、EXCLE、MATLAB这三种方法来处理实验数据。通过比较发现，逐差法的误差较大、计算过程繁杂。采用计算机软件处理数据结果准确度高，计算过程简单明了，可以有效提高学生的实验技能和科研水平。

【关键词】杨氏模量;逐差法;MATLAB;EXCLE

中图分类号： O4-39 文献标识码： A文章编号： 2095-2457（2019）31-0124-003

DOI：10.19694/j.cnki.issn2095-2457.2019.31.059

1 杨氏弹性模量实验原理

杨氏模量的测定方法是拉伸法。拉伸法是沿纵向加外力使材料产生形变的，它是研究最简单的弹性形变的方法。设有一根长为L，粗细均匀的铁丝，横截面积为S，受到沿长度方向上的外力F的作用时，铁丝的伸长量为△L。此时单位横截面积上受到的作用力为F/S，称之为胁强，也就是正向应力。铁丝在单位长度上的伸长量为△L/L，称之为胁变，也就是正向应变。正向应力与正向应变的比值就是杨氏模量，即：

Y=■·■（1）

2 实验仪器

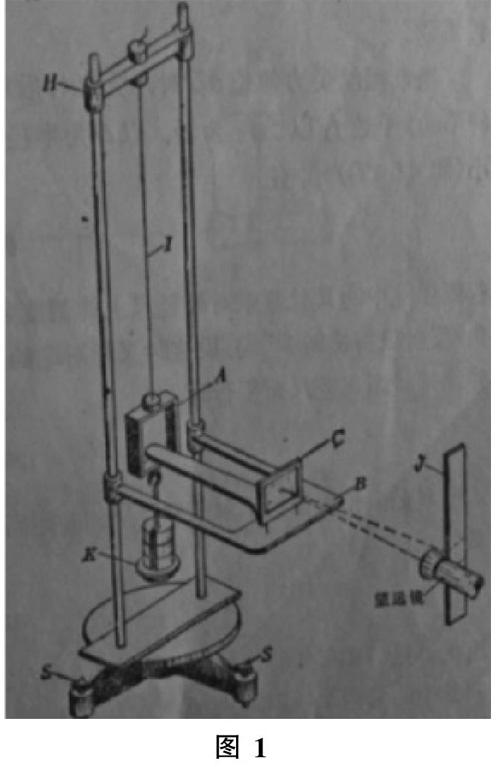
图1

2.1 杨氏模量仪

仪器装置如图1所示。三脚底座上装有两根平行立柱和调节螺母，固定底座上有水准泡。通过调节平衡螺母使水准泡处在中心位置，从而来判断底座是否调平。金属丝I的上端固定在立柱顶端横梁的螺钉中，下端系在托盘的钩上，托盘是用来放拉伸铁丝的砝码。立柱中间有一可以上下移动的平台，平台是用来安放光杠杆。平台正中有孔，孔中有可以滑动的卡金属丝的螺旋卡头，金属丝通过螺旋卡头并衔接在中间。

2.2 光杠杆及望远镜尺组

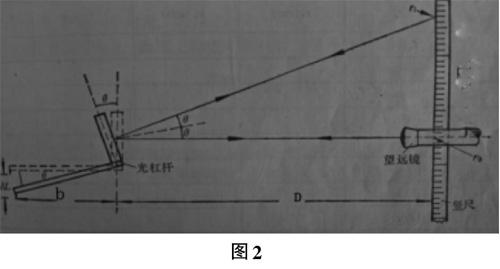
由于△L的变化太小，常规仪器是测不出来的，所以本实验用到的是光杠杆和望远镜。本实要用该测量系统测量铁丝的伸长量△L。三足支架后足尖到两前足间连线的垂直距离为b。镜面的正前方约1.5m处放望远镜及标尺。

图2

如图2所示，当所测物体未发生变化前，可从望远镜内读出标尺上的标度值n0，即水平读数。加砝码后金属丝的伸长量为△L，三足支架的后足随金属丝L的伸长随螺旋卡时下降△L。此时镜面以前足尖为支点向后转过θ角度，tgθ=■，这时由望远镜里读出标尺上的读数为n1，前后两次读数差为△n= n1-n0。[2]

由图2可以看出：tgθ=■，tg2θ=■。

实验中，△L很小，θ角度也很小，因而tgθ=θ，tg2θ=2θ，θ=■，2θ=■，将θ消去得： △L=■（2）

△L原为难以测量的微小量，通过光杠杆的放大作用，使之变为容易的测得的较大量：D、b、△n。

因为我们知道金属丝的截面积为S=■πd■，将之与（2）代入（1）两式可得：

Y=■（3）

3 实验过程

3.1 杨氏模量测定仪的调节

3.2 光杠杆及望远镜尺组的调节

1）粗调—调节光杠杆及望远镜、标尺中部在同一高度上。

2）镜外找像—缺口、竖尺、平面镜中标尺的像在一个平面内。

3）镜内找像—先调节目镜使叉丝清晰，在调节调焦钮看清标尺像直到无视差为准。

4）细调—对准标尺像的零刻度线附近的任意刻度线，并记录读数n。

4 实验数据处理

4.1 实验数据的记录

4.2 利用逐差法对数据进行处理

利用常规的逐差法解得：

杨氏模量

Y=■=■=1.752×1011Pa

相对误差：η=■100%=7.79%

4.3 利用EXCLE对数据进行处理

将公式Y=8FLD/（πd■b△n）=8mgLD/（πd■b△n）做一变形可得：

△n=（8LD/πd2bY）×F                     （4）

即△n随F的变化而变化。利用EXCLE可以计算出砝码所受重力和△n大小（见附件2）。

将砝码所受重力G与△n的值输入EXCLE可得如图3。

图3

由图3可以读出此直线的斜率k=0.0012。利用EXCLE可以计算出铁丝的长度L、镜面到标尺的距离D、后足尖到两前足尖连线的垂直距离b及铁丝的直径d的平均值。（见附件2）

利用EXCLE将L、D、b、d的平均值及k值代入Y=■中，得到Y=1.763×1011Pa。

相对误差：η=■×100%=7.21%

4.4 利用MATLAB对数据进行处理

同理，也是将公式Y=8FLD/（πd2b△n）=8mgLD/（πd2b△n）做一变形可得：

△n=（8LD/πd2bY）F 即△n随F的变化而变化。

实验数据处理的程序如下：

m=0：9;

F=m*9.8;

n1=0.16;

n2=0.1719;

n3=0.1839;

n4=0.1955;

n5=0.2070;

n6=0.2189;

n7=0.2293;

n8=0.2411;

n9=0.2523;

n10=0.264;

n11=0.1598;

n12=0.1720;

n13=0.1842;

n14=0.196;

n15=0.208;

n16=0.2192;

n17=0.231;

n18=0.2432;

n19=0.2532;

n20=0.264;

n21=（n1+n11）/2;

n22=（n2+n12）/2;

n23=（n3+n13）/2;

n24=（n4+n14）/2;

n25=（n5+n15）/2;

n26=（n6+n16）/2;

n27=（n7+n17）/2;

n28=（n8+n18）/2;

n29=（n9+n19）/2;

n30=（n10+n20）/2;

n31=n22-n21;

n32=n23-n21;

n33=n24-n21;

n34=n25-n21;

n35=n26-n21;

n36=n27-n21;

n37=n28-n21;

n38=n29-n21;

n39=n30-n21;

n=[0，n31，n32，n33，n34，n35，n36，n37，n38，n39];

plot（F，n）;

由该程序得到如图4。

再运行程序：

h=1;plot（F，n，h）;

可以得到图5，即可得到此直线的斜率k=0.0012。

图5

在MATLAB中输入程序：

L=[0.7401，0.741，0.7405，0.7405，0.7403];avg_L=mean（L）

輸出：avg_L =

0.7405

输入：D=[2.0604，2.061，2.0608，2.061，2.0604];

avg_D=mean（D）

输出：avg_D =

2.0607

输入：d=[0.000482，0.000489，0.000488，0.000481，0.000483];

avg_d=mean（d）

输出：avg_d =

4.8460e-04

输入：b=[0.07815，0.07815，0.07812，0.07807，0.07815];

avg_b=mean（b）

输出：avg_b =

0.0781

从而得到L、D、b及d的值，代入Y=■，即Y=1.767×1011Pa

相对误差：η=■100%=7.00%

5 结论

我们知道铁丝杨氏模量的实验参考值为Y■=1.90×10■Pa.本次实验的三种计算结果都分别是Y■=1.75×10■Pa，Y■=1.76×10■Pa，Y■=1.77×10■Pa。实验值和参考值之间明显存在差值，对应误差分别为η■=7.79%，η■=7.21%，η■=7.00%。究其误差原因：1）实验数据的不准确性。实验过程中，需在加完或减完砝码时，铁丝不晃动的时候读数，所以有可能在某一次实验时，忽略了此细节。2）实验室的金属丝用的时间太久。比起一根新的铁丝，实验室的铁丝经常用来实验，经常被拉伸，弹性性能大不如以前。实验结果就会和准确值之间存在差异。就实验数据处理的过程来看，用逐差法计算实验数据过程烦琐、计算量大，而EXCLE处理数据需要多个表格来计算各物理量。这种方法虽避免了人为计算的误差，但整个计算过程变得很混乱。MATLAB是通过输入相应的程序来计算物理量的。本篇文章的目的是找到一个误差最小的、过程简洁的数据处理方法并将之在实验中推广。由上述比较可以看出，MATLAB的误差较小，过程也相对来说较为简洁，可以考虑将MATLAB在今后的实验中做一推广。这一方法不仅可以很好地处理实验数据，也可以提高同学们的科研能力。但由于我们专业的学生对MATLAB的学习只停留在表面，再加上利用MATLAB编程本身就比较难。要想很好地将之运用到实验中是非常困难的。所以大学的课程设置中一定要将这些计算机软件的学习重视起来，让学生在运用这些软件时得心应手。

【参考文献】

[1]谢杨莹，秦玉霞，杨旭昕，叶全林.拉伸法测头发丝杨氏模量实验装置的改装[J].物理实验，2018，38（09）：51-54.

[2]刘志亮.用双臂电桥测金属丝杨氏模量的优化实验[J].物理通报，2018（07）：83-85.

[3]白冰.新的实验方法在大学物理实验课堂中的应用[J].新西部，2017（27）：145+152.

[4]饶益花，郭萍，管亮，李全.基于Matlab的金属丝杨氏模量测量的数据处理[J].大学物理实验，2004（04）：76-78.

[5]丁益明、徐扬子主编。大学生物理实验[M].基础与综合部分，北京：科学出版社，2008.

[6]高海林，拉伸法测金属杨氏模量实验的改进[J].2006，8.