线性脉冲系统的稳定性分析

周旺旺　方建安

【摘 要】对线性脉冲系统进行稳定性分析，首先是通过运用半张量积方法给出基于逻辑判断的线性脉冲系统的表达式，然后利用稳定性的判别方法，得到了该系统稳定的充分条件，接着运用定义和引理来对其进行证明，再给出数值例子，通过仿真来说明结果的有效性。

【关键词】脉冲系统;稳定性;半张量积;逻辑判断

中图分类号： TP13文献标识码： A 文章编号： 2095-2457（2019）31-0004-003

DOI：10.19694/j.cnki.issn2095-2457.2019.31.002

Stability Analysis of Linear Impulsive System

ZHOU Wang-wang FANG Jian-an

（College of Information Science and Technology， Donghua University， Shanghai 201620， China）

【Abstract】The stability analysis of linear impulsive system is carried out. Firstly， the expression of linear impulsive system based on logic judgment is given by using the semi-tensor product method. Then， the sufficient conditions for the stability of the system are obtained by using the method of stability judgment. Then， the definition and lemma are used to prove the stability of the system. Finally， numerical examples are given to illustrate the validity of the results by simulation.

【Key words】Impulsive system; Stability; Semi-tensor product; Logical judgment

0 引言

在發展变化过程中，自然界中的许多事物常常因受到短暂时间的干扰而发生快速的变化，如种群动力学中的动物的季节繁殖，渔业养殖与森林管理中的投放、种植、收获等，在这些过程的数学模拟中，这段发生快速变化的持续时间常常会被忽略，然后假设这个过程是瞬间完成的，这种瞬时突变现象通常被称为脉冲现象，其数学模型通常可归结为脉冲微分系统。在实际应用中我们总是希望，在受到外来干扰不太大时，系统能够在经过一个过渡过程后恢复到原来的平衡状态，这样，我们才能更好地控制系统，使其大体地可以按照预测的结果进行下去。例如，对于发射宇宙探测器，若不能在受到一定范围内的干扰后依然可以回归到原有轨道，那它的任务将不能完成，还有很多诸如此类的例子。鉴于脉冲系统在科技领域发挥着越来越重要的作用，这方面的研究引起很多学者专家的关注与重视。脉冲微分方程理论最早是由Millman和Myshkis在20世纪六十年开创性的提出来的[1]，成了数学界的一个新的分支，在接下来的20年，它也经过了不断发展[2]，1989年，首次出版的关于脉冲微分系统的著作“Theory of Impulsive Differential Equations”是由V.Lakshimikantham[3]等人对这些进行了系统的总结所完成的。文献[4]给出了系统平衡点和稳定性的定义，文献[5-6]中程代展教授提出了半张量积这一定理，使矩阵乘法不再局限于传统矩阵维数的要求，这样的话，任意两矩阵都可以相乘。之后，程代展教授等人将半张量积应用到逻辑系统中，将一个逻辑函数转化为等价矩阵、向量乘积的代数表达形式，从而解决了逻辑表达式的计算和处理问题，对逻辑处理给予了很大的帮助。文献[7]中范数的相关理论，用于构造辅助系统，使后面定理的验证得以实现。

脉冲系统的研究已经日趋成熟，于是我对线性脉冲系统的性质进行了具体的探究，所研究的线性脉冲系统具体可描述为

x（t）=Ax（t），t≠t■Δx（t■）=g（p■（x■（t■）），…p■（x■（t■）））Bx（t■）+■Cx（t■），t=t■x（t■■）=x■（1）

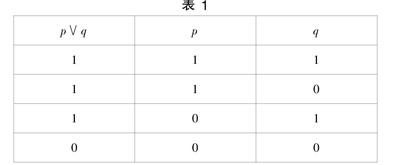
其中A、B、C 均为n阶矩阵，tk为第k次脉冲发生的时刻，x（t）和Δx（t）都为n维向量：x（t）=（x1，x2，…，xn）T∈Rn，Δx（t）=（Δx1，Δx2，…，Δxn）T∈Rn。关于脉冲时间序列{tk}■■，我们假定0

1 线性脉冲系统稳定性分析

1.1 预备知识

下面介绍一些定义、引理及符号，是后面的证明及验证过程所要用到的。

对于向量x=（x1，x2，…，xn）T∈Rn，‖x‖=■x■■■表示x的欧几里得范数。对于实对称矩阵A，λmax（A）（λmin（A））表示A的最大（最小）特征值。Rowi（A）（Coli（A））表示矩阵A的第i行（列），Row（A）（Col（A））表示矩阵A所有（行）列的集合。

为了方便后续的研究，对于逻辑值，我们定义如下等价的向量表达形式：

T=1～δ■■=[1 0]T，F=0～δ■■=[0 1]T，其中，δ■■是单位矩阵Ik的第i列。令Δk={δ■■|i=1，2，…，k}，则其表示单位矩阵所有列的集合。

接着，我们给出如下定义和引理：

定义1[5]：如果矩阵L∈Rm×n满足Col（L）？奂Δm，则我们称L为逻辑矩阵。我们将所有m×n逻辑矩阵组成的集合表示为Lm×n。

定义2[7]：矩阵Kronecker积符号为“？茚”，对任意两个矩阵A=（aij）m×n∈Rm×n，B=（bij）p×q∈Rp×q，它们的Kronecker积为：

A？茚B=■。

定义3[7]：μ（A）=■■=λ■■，其中‖·‖表示矩阵的诱导范数，A是正数阶矩阵，I是单位矩阵。

引理3[7]：根据μ（A）的定义，可得对于线性微分方程■（t）=Ax（t），状态变量x（t）满足：

■≤μ（A）‖x（t）‖。

定义4[6]：对于两个矩阵A∈Rm×n，B∈Rp×q，A与B的半张量积为

A∝B=（A？茚Iα/n）（B？茚Iα/p），

其中，α=lcm（n，p）是n与p的最小公倍数。

下面这个引理揭示了如何将一个逻辑函数转换为等价矩阵、向量乘积的代数表达形式，用于后面的理论探究。

引理4[6]：f（p1，p2，…，pr）∈Δ2是一个逻辑函数，其中p1，p2，…，pr∈Δ2是逻辑变量，则存在唯一一个2×2r的矩阵Mf∈Lm×n使得

其中，Col（Mf）？奂Δ2，而且值得注意的是∝■■p■？奂Δ■。我们称矩阵Mf为逻辑函数f的结构矩阵。需要注意的是，引理2中的逻辑函数f（p1，p2，…，pr）∈Δ2是一个二维向量[1 0]T或[1 0]T，若逻辑函数的值最终表达为“1”或“0”的标量值时，引理3中的代数表达形式可以写为

下面我们引入平衡点及稳定性的定义。

定义5[4]：对于系统

■=f（x）

若f（xe）≡0，则我们称xe为系统的平衡点。

易知线性系统

■（t）=Ax（t），

的平衡点是原点。

定义6[4]：对于系统

■=f（x）

的平衡点为x=0，如果对于任意的ε>0，都存在δ=δ（ε）>0，满足

‖x（0）‖<δ？圯‖x（t）‖<ε，？坌t>0

则该系统的平衡点是稳定的。

定义7[4]：对于系统

■=f（x）

的平衡點为x=0，如果系统的平衡点是稳定的，且可选择适当的正数δ，满足

‖x（0）‖<δ？圯■x（t）=0，

则该平衡点是渐近稳定的。

1.2 主要结论

我们从系统（1）的表达式可以看出，当不发生脉冲现象时，系统（1）的第一个式子是线性微分方程，通过求解得出x（t）的表达式;当发生脉冲现象时，系统（1）的第二个式子中Δx（tk）表示状态变量在脉冲发生后与发生前的差值，即Δx（tk）=x（t■■）-x（t■），k∈N■。当发生第k次脉冲现象，即t=tk时，有

Δx（t■）=g（p■（x■（t■）），…p■（x■（t■）））Bx（t■）

+■Cx（t■）

其中g：{δ■■，δ■■}n→{0，1}是一个逻辑函数，g是g的否定逻辑函数。比如，当g的逻辑值为0时，g的逻辑值为1;当g的逻辑值为1时，g的逻辑值为0。B，C是两种备选方案的脉冲效应的逻辑矩阵。pi：R→{0，1}是一个分段连续函数，定义如下：

pi（u）=δ■■～0，|u|≥c■δ■■～1，|u|

其中ci是一个阈值。

由引理3可知存在g的结构矩阵M使得下面这个等式成立：

g（p1（x1（tk）），…，pn（xn（tk）））=Row1（Mf）∝■■p■（x■（t■））

并且g的否定函数g可以表示为

■=Row2（Mf）∝■■p■（x■（t■））

令p（x（tk））为∝■■p■（x■（t■））。根据pi（u）的定义，我们知道pi（xi（tk））∈Δ2，i=1，2，…，n。然后再根据半张量积的定义，我们可以知道是p（x（tk））一个2n维向量，且p（x（tk））∈Δ■，设p（x（tk））的值为δ■■，即p（x（tk））=δ■■，它是一个第jk个分量为1其余分量为0 的单位向量。进而我们有

Δx（tk）=Row1（M）p（x（tk））Bx（tk）+Row2（M）p（x（tk））Cx（tk）

=M■Bx（tk）+M■Cx（tk）

=（M■B+M■C）x（tk）

其中，M■和M■分别表示矩阵M的第1行第jk个元素和第2行第jk个元素。下面，我们进一步推导可以得到：

M■B+M■C=B（M■？茚In）+C（M■？茚In）

=[B C]M■？茚InM■？茚In

=[B C]（Col■（M）？茚In）

最终Δx（tk）可以表示为以下形式：

Δx（tk）=[B C]（Col■（M）？茚In）x（tk）（2）

因此，当Col■（M）=10时，Δx（tk）=Bx（tk）;

同样，当Col■（M）=01时，Δx（tk）=Cx（tk）。

由此可以看出（2）的逻辑表达式与系统（1）中Δx（tk）的表达式是等价的。于是Δx（t■■）可以表示为下面的形式：

x（t■■）=x（t■■）+Δx（tk）

=[B+I C+I]（Col■（M）？茚In）x（t■■）

因此我们可以得到

另一方面，当t∈[tk，tk+1）时，由（1）式的第一个表达式

■（t）=Ax（t），

我们可以推出

x（t）=e■x（t■■）（4）

根据以上理论分析，我们得到下面系统稳定性的主要结论，并对这个定理进行证明。

定理：如果基于逻辑判断的线性脉冲系统（1）满足如下条件：

（i）■■[‖B+I‖‖C+I‖]Col■（M）<+∞;

（ii）μ（A）≤0;

则系统（1）的平衡点是稳定的。

若把条件（ii）加强为：（ii*）μ（A）<0时，则系统（1）的平衡点是渐近稳定的。

证明：为了研究系统的渐近稳定性，我们先考虑如下系统：

■（t）=μ（A）u（t），t≠t■u（t■■）=[‖B+I‖‖C+I‖]Col■（M）u（t■）u（t■■）=u■≥‖x■‖（5）

其中函数u：[t0，∞）→R。

当t∈[tk，tk+1）时，由系统（5）的第一个表达式可以推出

u（t）=e■u（t■■）。

再根据系统（5）的第二个表达式可得

u（t）=e■[‖B+I‖‖C+I‖]Col■（M）u（t■）

再对u（tk）进行依次递推，可以得到

u（tk）=e■u（t■■）

=e■[‖B+I‖‖C+I‖]Col■（M）u（t■）

……

u（t2）=e■u（t■■）

=e■[‖B+I‖‖C+I‖]Col■（M）u（t■）

u（t1）=e■u（t■■）

=e■u0

因此通过从下到上依次带入可得

u（t）=e■■[‖B+I‖‖C+I‖Col■（M）]u■

根据条件（i）和（ii）可知系统（5）的平衡点是稳定的。当系统满足条件（i）和（ii*）时，系统（5）的平衡点是渐近稳定的。

由引理3可知

■≤μ（A）‖x（t）‖

由系统（5）可知

■≤μ（A）u（t）

uo≥‖x0‖

于是，根据比较原理[3]以及式（4）可知，当t≥t0时，有0<‖x（t）‖≤u（t）。

这表明系统（1）的平衡点是稳定的，当且仅当系统（5）的平衡点是稳定的。系统（1）的平衡点是渐近稳定的，当且仅当系统（5）的平衡点是渐近稳定的。因此定理得证。

2 数值例子

下面通过举一个具体的例子来验证定理，证实其有效性。首先设定x=（x1，x2，x3）T∈R3是三维向量，这里我选取初值x0=（1.5，-0.5，2）T，脉冲发生周期为0.5，还有

A=■

经过计算得到其特征值分别为λ=-3，λ2=-4，λ3=-2

系统（1）的逻辑函数如下所示：

g（p1，p2，p3）=（p1∨p2）？圮p3

其中“∨”表示“析取”逻辑关系，若p，q为两个逻辑变量，则有如下真值表：

表1

逻辑关系“∨”对应的逻辑矩阵为

Md=■

“？圮”表示“等价”逻辑关系，有如下真值表：

表2

逻辑关系“？圮”对应的逻辑矩阵为

Me=■

对于逻辑函数g，存在2×8维结构矩阵M，使得

g（p1，p2，p3）=M∝■■pi

其中

M=Me∝Md=■

我们选取B=-■I3，C=-■I3，I3是3阶单位矩阵，易知这里满足条件（i），我们这里阈值取为c1=c2=c3=0.1，于是

μ（A）=■■=λ■■=-1.0944<0，

满足条件（ii*），因此根据定理，我们可知系统的平衡点是渐近稳定的。下面是通过MATLAB仿真所得的系统状态轨迹图，如图1所示：

图1 x随时间t的轨迹

3 结论

本文通过对线性脉冲系统进行稳定性分析，得到了系统稳定的定理判据，该研究分析可以在工程中发挥比较大的作用，在面对突发事件时，可以对系统进行控制，使其根据逻辑判断自动选取合理的方案，使损失减小，这是一种比较经济快速地选择。

【参考文献】

[1]Millman V D， Myshkis A D. On the stability of motion in the presence of impulses， Sib Math J，1960，1（2）： 233-237.

[2]Samoolenko A. M， Perestyuk N A. Differential equations with impulse effect， Kiev：Visca Skola， 1987.

[3]Lakshmikantham V， Bainov D， Simeonov P. Theory of impulsive differential equations， World Scientific， Singapore， 1989.

[4]朱義胜.非线性系统. 北京：电子工业出版社，2011：74

[5]Cheng D Z， Qi H S. A Linear representation of dynamics of Boolean Networks，IEEE Trans.Autom.Control， 2010， 55（10）：2251-2258.

[6]Cheng D Z， Qi H S. Analysis and control of Boolean networks：a semi-tensor product approach， Springer-Verlag London， 2011， 37（5）：1352-1356.

[7]Gustaf S. The logarithmic norm history and modern theory. Bit Numerical Mathematics， 2006， 46：631-652.