基于LSTM神经网络的乌鲁木齐市流感样病例的预测研究

龚风云　王凯

【摘 要】目的：分析乌鲁木齐市流感样病例月发病数的变化趋势，建立长短期记忆（LSTM）模型，对流感样病例例数数进行预测，为乌鲁木齐市流感的预防与控制提供科学依据。方法：利用2015年1月-2018年3月乌鲁木齐市的每月气象数据、流感样病例监测数据，采用单变量LSTM模型和多变量LSTM模型对乌鲁木齐市流感样病例例数的时间序列进行预测，使用RMSE和MAE值评价不同方法的预测精度。结果：单变量LSTM模型和多变量LSTM模型的RMSE值分别是66.17和56.91;MAE值分别是60.42和39.07。与单变量LSTM模型相比，多变量的LSTM模型预测效果较好。结论：本研究所建立的多变量LSTM模型能较好地预测ILI病例数的发病趋势，为流感监测和预防控制提供依据。

【关键词】LSTM;流感样病例;气象因素;预测

中图分类号： TP393.0;TP183 文献标识码： A 文章编号： 2095-2457（2019）31-0020-003

DOI：10.19694/j.cnki.issn2095-2457.2019.31.009

Prediction of influenza-like cases in urumqi based on LSTM neural network

GONG Feng-yun1 WANG Kai2*

（1.College of Applied Mathematics，Xinjiang University of Finance and Economis， Urumqi Xinjiang 830012， China;

2.College of Medical Engineering and Technology，Xinjiang Medical University， Urumqi Xinjiang 830011， China）

【Abstract】[Objective]To analyze the change trend of the monthly incidence of influenza-like cases in Urumqi， establish long-short term memory（LSTM） model，and predict the number of influenza-like cases， so as to provide scientific basis for the prevention and control of influenza in Urumqi.[Methods]Monthly meteorological data and influenza-like case monitoring data from January 2015 to March 2018 in Urumqi were used to predict the time series of influenza-like cases in Urumqi using univariate LSTM model and multivariate LSTMmodel， RMSE and MAE values were used to evaluate the prediction accuracy of different methods.[Results]RMSE values of univariate LSTM model and multivariate LSTM model are 66.17 and 56.91 respectively.The MAE values are 60.42 and 39.07 respectively.Compared with the single-variable LSTM model， the multivariable LSTM model has a better predictive effect. [Conclusion] The multivariate LSTM model established in this study can better predict the incidence trend of ILI cases， providing a basis for influenza surveillance， preventionand control.

【Key words】LSTM; Influenza-like cases; Meteorological factors; Prediction

流行性感冒简称流感，是由流感病毒引起的一种传染性呼吸道疾病[1]。流感病毒主要通过空气传播，如咳嗽、喷嚏等[2]。据统计，全球每年约有10%～20%的人群因流感的季节性流行而感染流感，其中300万～500万人为重症病例，25万～50万人为死亡病例[3]。流感的流行不仅对人群健康造成严重威胁，也对社会产生了巨大的经济损失[4]。在美国，流感每年的总成本超过100亿美元，而未来的流感大流行估计直接和间接成本高达数千亿美元[5]。Yang J等[6]一项覆盖全国范围的研究显示，个人流感门诊病例的平均费用为$155，流感住院病例的平均费用为$1511。在疾病高峰期，诊所和医院不堪重负。接种流感疫苗和阻碍传播途径是预防流感有效的方法[7]。新疆乌鲁木齐市是流感多发地之一，该市作为国家级流感监测点，对流感样病例（influenza-like illness，ILI）进行了长期持续的监测[8]。为了帮助政府、医院、诊所、制药公司和其他公司有效地控制流感爆发，并及时限制传播途径，本研究使用LSTM模型对乌鲁木齐市ILI例數数据进行训练拟合、分析及预测，并比较预测精度。

1 资料与方法

1.1  ILI定义

发热（体温≥38℃）、伴咳嗽或咽痛之一者[9]。

1.2 资料来源

2015年1月—2018年3月乌鲁木齐市的每月ILI例数来源于“中国疾病预防控制信息系统流感监测信息子系统”。气象数据资料来自乌鲁木齐市气象局，主要包括月平均气温（℃）、月降水量（mm）、月平均气压（hpa）、月平均最大气压（hpa）、月平均最小气压（hpa）、月平均相对湿度（%）、月平均风速（m/s）、月日照时数（h）。

1.3 长短期记忆人工神经网络（long-short term memory，LSTM）

LSTM是一种改进的时间循环神经网络（recurrent neural network，RNN）[10]，它的提出解决了传统循环神经网络在学习过程中由于输入序列过长带来的梯度消失问题[11]。一个LSTM单元包括细胞状态（cell state）、输入门（input gate）、遗忘门（forget gate）、输出门（forget gate），且LSTM神经元的三个门的激活函数均为 Sigmoid[12]。

1.4 模型预测效果的比较

本文通过计算测试集的均方根误差（Root Mean Square Error，RMSE）和平均绝对误差（Mean Absolute Error，MAE）来定量地评价模型拟合及预测效果。该计算公式如下：

RMSE=■

MAE=■■|Y■-Y■|

式中，Y1t和Y2t均分别为t时刻的观测值和模型输出值，n为数据点个数。

1.5 统计分析

使用Python3.0和R3.6.1软件建立LSTM模型，其中各变量之间的相关性分析均采用了统计学中的Spearman相关。检验水准α=0.05。

2 结果

2.1 描述性分析

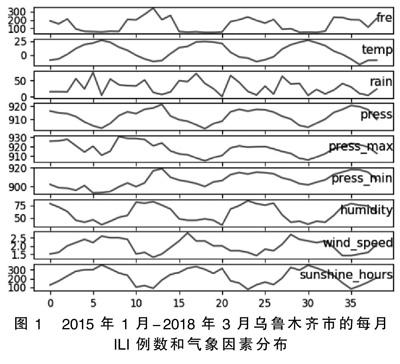
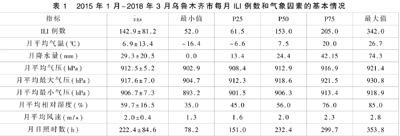
2015年1月-2018年3月乌鲁木齐市的ILI病例总数为5572例，月平均发病数约为143例。其中，月ILI例数、月平均气温（℃）、月降水量（mm）、月平均氣压（hpa）、月平均最大气压（hpa）、月平均最小气压（hpa）、月平均相对湿度（%）、月平均风速（m/s）、月日照时数（h）分别用fre、temp、rain、press、press_max、press_min、humidity、wind_speed、sunshine_hours表示。该时间序列图显示，流感样病例数呈现明显的季节性，冬春季发病数明显多于夏秋季。月平均气温、月降水量、月平均风速和月日照时数在冬春季偏低，夏秋季偏高，而月平均气压、月平均最大气压、月平均最小气压和月平均相对湿度在冬春季偏高，夏秋季偏低。见图1。2015年1月—2018年3月乌鲁木齐市的月平均气温、月降水量、月平均气压、月平均最大气压、月平均最小气压、月平均相对湿度、月平均风速、月日照时数的均值分别为6.9℃、29.3mm、912.5hPa、917.6hpa、906.7hpa、59.7%、2.0m/s、222.4h。见表1。

2.2 LSTM模型分析

2.2.1 单变量LSTM模型

由于LSTM不需要对时间序列进行平稳性和白噪声检验，可以直接建立模型。所以，本文首先对数据进行预处理，将时间序列数据转化为学习数据，并且对数据进行归一化处理。然后将数据集分为训练集和测试集，将2015年1月-2016年1月的数据作为训练集，2016年2月-2018年3月的数据作为测试集。最后建立LSTM模型，本文设置模型的隐藏层数为4，输入层和输出层分别为1和1;时间步长（time_step）设置为1。

图1 2015年1月-2018年3月乌鲁木齐市的每月ILI例数和气象因素分布

2.2.2 多变量LSTM模型

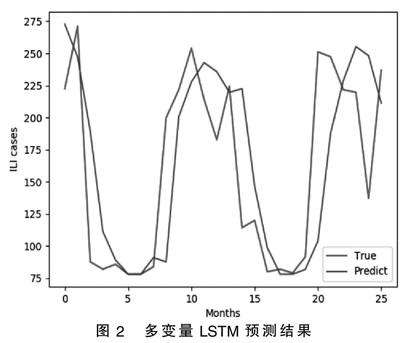
由于单变量LSTM的预测结果并不太好，所以本文对单变量LSTM的输入层与隐藏层进行了改变，进而构建了一个可以输入多个序列的多变量LSTM模型。本文设置的多变量LSTM模型的隐藏层数为50;输入层和输出层分别为8和1;每批次训练样本数（batch_size）设置为72;时间步长（time_step）设置为1;在 输入特征时需要将tensor转成三维作为LSTM cell的输入。结果见图2。

图2 多变量LSTM预测结果

2.2.3 模型评价

从表2可以看出，与单变量LSTM模型相比，纳入多个变量的LSTM模型预测的RMSE和MAE略小。其中，多变量的LSTM模型预测的RMSE降低了9.26，预测的MAE降低了21.35。表明多变量LSTM模型可以提高模型的预测精度。

表2 单变量LSTM模型和多变量LSTM模型的预测精度比较

3 讨论

本研究采用时间序列分析方法，分析了2015年 1月～2018年3月新疆乌鲁木齐市ILI例数的发病趋势。时间序列模型通过使用不同的特性可以分为3种类型[5]。第一类模型是自回归模型，它使用过去的患者数量作为特征（“xs”），并预测未来的患者数量作为响应（y）。典型的例子包括自回归综合移动平均（ARIMA）模型和向量自回归模型（VAR）。第二类模型使用其他参数（如温度、湿度等）代替过去的流感数据作为回归模型（如线性回归、随机森林等）的特征。著名的例子是“谷歌流感趋势”，它使用搜索引擎查询数据作为特征和线性回归模型。第三类模型是第一类和第二类的组合。它使用过去流感患者的数量作为特征（如第一种类型）和回归模型（如第二种类型）。本研究采用了第三种模型类型，长短期记忆（LSTM）模型来预测流感的爆发。

从描述性分析结果来看，2015年1月—2018年3月乌鲁木齐市的ILI发病数呈现冬春季高发的特点，该特点不同于南方地区流感流行趋势，南方春季或初夏流感活动较为活跃，这与南北方气候差异相关。已有研究表明，地理位置、气候条件的差异是造成北方地区与南方地区流感流行时间不同的主要因素[13]。由于乌鲁木齐市位于中国西北地区，是温带大陆性气候[14]。温带大陆性气候特点主要包括冬夏2季时间较长，春秋2季时间较短，且冬季寒冷，夏季炎热，年降水量少，比较干旱[15]。所以其发病呈冬春季高发的特点。

从LSTM模型结果分析来看，本文将气象因素中的多变量LSTM模型概念引入到ILI发病数的预测中，为一般基于单变量 LSTM流感样病例预测模型加入了更多气象因素特征，不再仅仅将ILI例数看作为一个简单的数学概念上的时间序列。适当使用多变量LSTM模型可能有助于预测目前和近期的流感传播。由于本文现有的流感数据有限，所以，流感预测模型的准确性还有待提高。但是，与单变量LSTM模型相比，纳入多个变量的LSTM模型预测的RMSE和MAE略小，说明多变量LSTM模型可以用于ILI发病数的预测，同时为公共卫生人员提供一个相对准确的参考点，进而对预防和控制流感的流行提出相关性建议。

然而，本文的研究也有一些不足。预测模型的准确性还有待提高，造成这个结果的可能原因是数据量较少，研究下一步将扩大样本量，再次對比单变量LSTM模型与多变量LSTM在预测疾病发病数上的精度。尽管多变量LSTM模型在预测精度上没有明显的优势，但是多变量LSTM模型也为预测ILI例数提供了新的方法。

【参考文献】

[1]谭娅文，万海同，何昱，杜海霞，杨洁红，彭学谦，周惠芬.中药抗流感病毒的作用及机制研究进展[J].中国现代应用药学，2019（16）：2095-2099.

[2]WHO，“Influenza（Seasonal），”http：//www.who.int/mediacentre/factsheets/fs211/en/index.html.

[3]崔永梅，杜中强，侯莹.孕妇感染甲型H3N2流感死亡病例的病因学分析[J].中国药物与临床，2019，19（5）：834-835.

[4]李文娟，王大燕.我国流感疾病负担相关研究进展[J/OL].中国人兽共患病学报：1-6[2019-08-31].http：//kns.cnki.net/kcms/detail/35.1284.R.20190723.1447.004.html.

[5]Jie Z ， Kazumitsu N . A comparative study on predicting influenza outbreaks[J]. BioScience Trends， 2017， 11（5）：533-541.

[6]Yang J，Jit M，Leung KS， et al.The economic burden of influenza-associated outpatient visits and hospitalizations in China： a retrospective survey [J]. Infect Dis Poverty，2015，4：44.

[7]张慕丽，彭质斌，郑建东， 等.中国儿童流感疾病负担和疫苗应用现状[J].中华实用儿科临床杂志，2019，34（2）：91-97.

[8]高枫，阿不都热依木，樊旭成，等.2016-2017年乌鲁木齐市流感监测结果分析[J].医学信息，2018，31（19）：134-136.

[9]中华人民共和国卫生部.全国流感监测方案（2010年版）[J].国际呼吸杂志，2011，31（2）：85-88.

[10]张春露.基于Tensorflow的LSTM在太原空气质量AQI指数中的分析与预测[D].中北大学，2019.

[11]裴大卫，朱明.基于多因子与多变量长短期记忆网络的股票价格预测[J].计算机系统应用，2019，28（8）：30-38.

[12]杨意豪，王梅，左铭.基于深度LSTM的甲亢疾病发展预测及应用系统[J].智能计算机与应用，2019，9（4）：128-131.

[13]蒲玉娇. 2012一2017年乌鲁木齐市流感流行特征与病原学监测分析[D].新疆：新疆医科大学，2018：36-37.

[14]LI J ， LI XM . Response of stomatal conductance of two tree species to vapor pressure deficit in three climate zones[J]. J Arid Land， 2014， 6（6）：771-781.

[15]陶燕，顾天毅，王砚，等.兰州市城关区流行性感冒与气象因素的时间序列[J].兰州大学学报（自然科学版），2018，54（1）：137-142.