钢砧的量值传递及影响量的分析与研究

郭贵勇　马兴

【摘 要】介绍了钢砧的工作原理和用途，建立了钢砧的测量模型，分析了各不确定度分量主要来源。结合测量实例具体数据，对其合成不确定度进行分析评定，对各不确定度分量进行计算并得出合成不确定度和扩展不确定度，最终可得出该项目的校准测量能力，为我国建筑和交通等行业提供的技术支撑。

【关键字】钢砧;量传传递;影响量;不确定度评定

中图分类号： TH871 文献标识码： A 文章编号： 2095-2457（2019）31-0087-003

DOI：10.19694/j.cnki.issn2095-2457.2019.31.040

The Analysis and Research on Performance Impact and Valve Transfer for Steel Anvil

GUO Gui-yong1，2 MA Xing1，2

（1.Fujian Metrology Institute， Fujian Fuzhou 350003， China;

2.Fujian Provincial Key Laboratory of Force Measurement， Fujian Fuzhou 350100， China）

【Abstract】This paper introduces the working principle and application of steel anvil， establishes the measurement model of the calibration results of steel anvil， analyzes the main sources of each uncertainty component， analyzes and evaluates the synthetic uncertainty combined with the concrete data of the measurement example， calculates each uncertainty component， obtains the synthetic uncertainty and extended uncertainty. Finally， the calibration and measurement ability of the project can be obtained. Overall， this paper can provide strong technical support for construction， transportation and other industries in our country.

【Key words】Steel Anvil; Valve Transfer; Performance Impact; Evaluation of Uncertainty

0 引言

钢砧是对混凝土，砂浆，砖等回弹仪进行校验的检验工具。钢砧各部件由优质钢及优质工具钢制成。钢砧作为检验工具，被弹击试验5000次-8000次后，可将砧芯连同砧体在平面磨平整再用。

1 钢砧的校准

钢砧测定将钢砧放置于金属表面洛氏硬度计检定试台上，其支承面应与硬度计试台台面研合，在钢砧标准块的工作面上测定4点，第1点不算，其余3点均匀分布，取其平均值即为钢砧标准块的示值;将钢砧水平居中放置于电子台秤上，重复测量三次，取其平均值即为钢砧质量。使用电子数显示卡尺，测量钢砧直径，测量三次取测量值的平均值。使用电子数显示卡尺，测量砧芯直径，测量三次取测量值的平均值。

2 钢砧硬度标准块的标准不确定度分量的评定

2.1 测量模型：h=h

式中：h——钢砧硬度

h——钢砧硬度三次测量值的平均值

2.2 标准不确定度分量的评定

1）输入量h的标准不确定度u（h）的评定：其不确定度来源主要是测量重复性引入的不确定度ua（h），可以A类方法评定ua（h）;洛氏硬度計引入的不确定度ub（h），可以B类方法评定ub（h）。

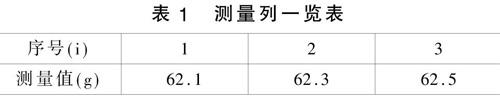
（1）选取一钢砧，用洛氏硬度计对其上连续进行3次测量，得到测量列为表1所示：

表1 测量列一览表

其所求的平均值：h=■■h■=62.3HR

单次实验标准偏差：极差法计算（系数C=1.69）：s=0.4/1.69=0.24HR实际测量中是在重复性条件下测量3次，取其算术平均值为测量结果。

则ua（m）=■=0.14HR

（2）根据标准洛氏硬度计的扩展不确定度不大于1.5HR，包含因子k=2，则可以用B类方法评定：

ub（h）=■=■=0.87HR

（3）把ua（h与ub（h）两项合成，则u（h）=■=0.88HR

2.3 合成标准不确定度的评定

2.3.1 灵敏系数：由h=h得

c1=■=1

2.3.2 标准不确定度汇总表，见表2。

表2 标准不确定度分量一览表

2.3.3 合成标准不确定度的计算：

uc（h）=uc（h）=1.8HR

2.4 扩展不确定度的评定：取包含因子k=2，则U=k·uc=1.8HR

2.5 扩展不确定度的报告与表示

钢砧硬度测量结果扩展不确定度为U=0.4HR。它是由合成标准不确定度uc=0.88HR和包含因子k=2之乘积得到。

钢砧硬度测量结果不确定度评估

钢砧硬度测量范围为（50～70）HRC，其测量不确定度如表3。

表3 标准不确定度汇总表

3 钢砧质量的标准不确定度分量的评定

3.1 数学模型：m=m

式中：m——钢砧质量

m——钢砧质量三次测量值的平均值

3.2 标准不确定度分量的评定

3.2.1 输入量m的标准不确定度u（m）的评定：其不确定度来源主要是測量重复性引入的不确定度

ua（m），可以A类方法评定;电子天平准确度引入的不确定度ub（m），可以B类方法评定。

ua（m），可以A类方法评定ua（m）;电子天平准确度引入的不确定度ub（m），可以B类方法评定ub（m）。

（1）选取一钢砧，在电子台秤上连续进行3次测量，得到测量列为表4所示。

表4 测量列一览表

其所求的平均值：

m=■∑■■m■=45010g

单次实验标准偏差：极差法计算（系数C=1.69）：s=0.0/1.69=0.00g，实际测量中是在重复性条件下测量3次，取其值为测量结果。

测量重复性引入的不确定度可忽略不计，则ua（m）=0.00g。

（2）电子台秤的准确度应大于15.0g，则可以用B类方法评定：

ub（m）=■=■=4.4g

ub（m）=0.010%

（3）把ua（m）与ub（m）两项合成，则

u（m）=■=0.010%

3.3 合成标准不确定度的评定

3.3.1 灵敏系数：由m=m得c1=■=1

3.3.2 标准不确定度汇总表，见表5。

表5 标准不确定度分量一览表

3.3.3 合成相对标准不确定度的计算：

uc（m）=uc（m）=0.010%

3.4 相对扩展不确定度的评定：取包含因子k=2，则Urel=k·uc=0.02%

3.5 扩展不确定度的报告与表示

钢砧质量测量结果相对扩展不确定度为Urel=0.02%。它是由合成相对标准不确定度uc=0.010%和包含因子k=2之乘积得到。

钢砧质量测量结果不确定度评估

钢砧质量质量测量范围为（10～60）kg，其测量不确定度如表6。

表6 标准不确定度汇总表

4 钢砧直径测量结果的不确定度评定

4.1 测量模型：D=D

式中：D——钢砧直径

D——钢砧直径三次测量值的平均值

4.2 标准不确定度分量的评定

（1）输入量D的标准不确定度u（D）的评定：其不确定度来源主要是测量重复性引入的不确定度，可以A类方法评定u（D）。

（2）选取一钢砧，以电子数显卡尺对钢砧直径连续进行3次测量，得到测量如表7所示。

表7 测量列一览表

其所求的平均值：D=■■D■=145.2mm

单次实验标准偏差：极差法计算（系数C=1.69）：s=0.1/1.69mm=0.06mm

实际测量中是在重复性条件下测量3次，取其值为测量结果。

则u1（D）=■=0.035mm

（3）电子数显卡尺的最大允许误差为±0.03mm，估计为均匀分布，其引入的标准不确定度为：

u2（D）=■=■=0.018mm

（4）把u1（D）与u2（D）两项合成，则u（D）=■=0.04mm

4.3 合成标准不确定度的评定

4.3.1 灵敏系数：由L=L得

c1=■=1

4.3.2 标准不确定度汇总表，见表8。

表8 标准不确定度分量一览表

4.3.3 合成标准不确定度的计算：

uc（D）=uc（D）=0.04mm

4.4 扩展不确定度的评定：取包含因子k=2，则U=k·uc=0.1mm

4.5 扩展不确定度的报告与表示

测量钢砧直径时，其标准值测量结果扩展不确定度为U=0.1mm。它是由合成标准不确定度uc=0.04mm和包含因子k=2之乘积得到。

5 砧芯直径测量结果的不确定度评定

5.1 按照上述同样方法对砧芯直径进行测量，标准不确定度汇总表，见表9。

表9 标准不确定度分量一览表

5.2 扩展不确定度的评定：取包含因子k=2，则U=k·uc=0.1mm

5.3 扩展不确定度的报告与表示

测量砧芯直径时，其标准值测量结果扩展不确定度为U=0.1mm。它是由合成标准不确定度uc=0.04mm和包含因子k=2之乘积得到。

对钢砧、砧芯直径测量结果的测量不确定度评估：

钢砧、砧芯直径测量范围为（25～200）mm，其测量不确定度如表10。

表10 标准不确定度汇总表

6 结语

保证钢砧的准确性，通过校准等方法实现量值的溯源性，在建筑和交通等行业的质量控制中起到重要作用;本文介绍我院对钢砧进行校准方法和不确定度评定方法。

【参考文献】

[1]中华人民共和国交通运输部.JJG（交通）107-2012，《杠杆压力仪》[S].北京：人民交通出版社，2012.

[2]张海红.福建省回弹法检测高强混凝土抗压强度的试验研究[J].福建建材.2009（05）.

[3]陈亚亮.回弹法检测砌体中普通粘土砖抗压强度试验研究[J].福建建设科技.2006（04）.