利用拖线阵运动特性的阵形估计方法

奚 畅 蔡志明 袁 骏

(海军工程大学电子工程学院 武汉 430033)

0 引言

拖线阵声呐对目标搜索、定位、跟踪、攻击过程中，拖船常需要进行战术机动，这必然造成拖线阵阵形畸变。如果在阵列信号处理时仍假设拖线阵直线形态，将严重影响拖线阵对弱目标的探测能力及方位估计精度，制约声呐系统整体性能的发挥。因此，有效估计阵形是提高机动条件下拖线阵探测性能的关键。

国内外学者提出了许多阵形估计方法，但应用于工程实际时往往存在困难。声学计算类阵形估计方法[1]无法回避的问题是阵列采样数据的信噪比和快拍数难以满足要求，并且不具备拖缆段阵形估计能力。基于阵中嵌入的姿态传感器的阵形估计方法[2]原理相对简单，但估计效果受到传感器数量和精度的限制，在硬件实施上代价较大。基于流体力学原理的阵形估计方法[3]不依赖外部声学环境，不需要在硬件上对基阵进行特殊设计，可以估计包括拖缆段和声阵段的全阵流形。Ablow模型[4]是典型的流体力学类阵形估计方法，其缺陷在于估计频率的选取、空间网格的划分、较复杂的拖船机动均可能造成雅克比矩阵求逆困难，导致求解发散。

针对经典流体力学类方法稳定性和可靠性欠佳问题，本文基于流体力学原理，分析转向机动过程中拖线阵上各点的运动特性，探究拖线阵上相邻两点沿阵切线方向的变化规律，建立一种工程应用前景较好的阵形估计方法。

1 稳态振荡响应特性计算

1.1 零浮力缆情况

Paidoussis[3]在惯性坐标系下分析柔性细长圆柱体微元段的受力平衡情况，建立了流体中零浮力缆的运动方程(Paidoussis方程)为

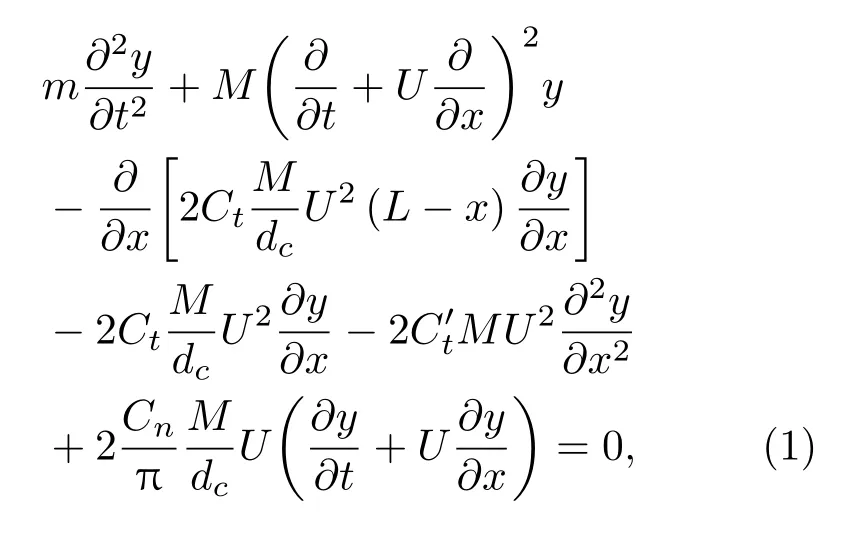
式(1)中，m是单位长度的缆质量，M是单位长度缆等体积的流体质量，dc是缆直径，L是缆长，U是缆轴向水流速度，Ct和Cn分别是缆的切向和法向阻力系数，C′t是缆尾部的形阻系数，当尾部处于自由状态时该系数为零。对式(1)进行无因次处理可得

其中，

τ=tU/L是无因次时间变量；ξ=x/L是无因次缆上位置，ξ= 0 表示拖点，ξ= 1 表示缆尾；η(ξ,τ)是缆上位置和时间的函数，表示ξ位置在τ时刻的位移；∆可为任意数。

拖船做简谐运动且缆达到稳态时，缆上各点均做相同频率、不同振幅的简谐运动。在式(2)中带入拖船位移方程，得到零浮力缆的稳态振荡响应公式[5]：

其中，

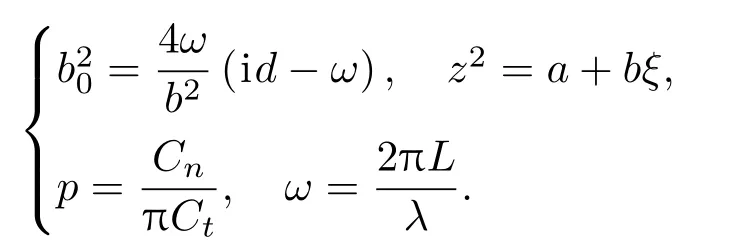
Jp是p阶贝塞尔函数；λ是拖船简谐运动的波长；ω是无因次频率；|v(z)|表示归一化振幅，tan−1[Im(v(z))/Re(v(z))]表示相对于拖船的相位差。

拖船回转运动情况下，达到稳态的缆上各点做相同圆频率、不同半径的回转运动，且拖船回转运动与简谐运动的拖船位移方程相同。因此当缆满足拖缆坐标系条件(螺旋状缆首尾相位差小于π)时，稳态振荡响应公式也可用于拖船回转机动的情况，此时无因次频率ω= πL/(2R)，R是回转半径。根据缆上各点归一化振幅和相对于拖船的相位差，即可得到拖船回转运动时缆的稳态流形。

1.2 拖线阵情况

式(3)只适用于单一物理属性的缆，拖线阵的拖缆段和声阵段的物理属性不同，计算拖线阵稳态振荡响应特性时需要分别计算拖缆段和声阵段的振荡特性，再将二者拼接起来。

计算拖缆段稳态特性时，应采用文献[5]方法，首先利用式(4)对切向及法向阻力系数进行调整，其次通过式(5)所示的单位长度缆切向阻力公式计算直行状态下拖缆段切向阻力以及声阵段切向阻力，进而由式(6)计算得到声阵段形阻系数Ct′。将调整后的阻力系数Cn∗、Ct∗以及形阻系数Ct′带入式(3)即可得到拖缆段振荡响应特性。

式(4)中，ϕ和θ分别是缆与流体之间的垂直夹角和水平夹角。缆与流体的水平夹角是时变的，且与无因次频率、缆上位置相关，难以从理论角度分析。海试数据表明，对于不同无因次频率的简谐运动阵上各点平均水平夹角在1.1◦∼18.9◦区间内[5]，本文在计算时假设θ= 10◦。垂直夹角可由放缆长度和嵌入缆中的深度传感器数值计算得到。

计算声阵段稳态特性时，需要将拖缆段等效为一定长度的声阵，将声阵段和拖缆等效段作为一体进行计算，得到整体的响应特性再截取声阵段部分即可，等效原则是对于某一波长的振荡，拖缆等效段尾端与拖缆段尾端的振幅相等，即保证声阵段首端的运动轨迹一致。

2 转向机动中的拖线阵运动规律

实际侦测过程中，常用的战术机动模式是在直行的基础上调整操舵角度，令拖船以一固定转弯半径进行转向，调整到指定航向后将舵角归零继续直航，完整航迹由圆弧和圆弧两端的切线组成，本文将此称为转向机动。

对于转弯角度较大的转向机动，拖船转向后拖线阵上各点依次受到影响，脱离直行稳态并逐渐进入回转稳态；拖船结束转向开始直行后，阵上各点依次脱离回转稳态并逐渐变为直行稳态。因此可将拖船转向机动过程中拖线阵上各点运动状态变化情况归纳为“直行稳态-过渡态-回转稳态-过渡态-直行稳态”。阵上各点在回转稳态的运动特性可利用第1 节方法计算得到。以阵尾端为例，各运动阶段示意图如图1所示。

图1 拖线阵运动状态示意图Fig.1 Motion state of towed linear array

图1中尾端在A点脱离直行稳态，在B点进入回转稳态，在C点达到圆弧顶点，在D点脱离回转稳态，在E点进入直行稳态。用TAB表示从A点运动到B点所需时间，由阵形仿真结果可知，TAC与TCE基本相等，TBC与TCD基本相等，因此可假设脱离/进入直行稳态和回转稳态的时间关于圆弧顶点对称，仿真算例将在第4节给出。

基于上述假设，若能求得B、D两点中任一点和A、E两点中任一点时刻，即可得到各运动阶段的分界时刻。

3 拖线阵上各点响应时间计算

拖船转向机动的过程中，阵上各点受到拖船转向的影响时脱离直行稳态，受到拖船直行的影响时脱离回转稳态，若能计算阵上各点对于拖船转向和直行的响应时间，即可确定图1中A点和D点。

对于式(2)所示无因次Paidoussis 方程， 考虑缆尾处于自由状态即C′t= 0 的情况，ξ ∈[0,1−dc/(2CtL))时a+bξ <0，β2−(a+bξ)>0，此时式(2)属于双曲型二阶偏微分方程。常规拖线阵满足dc/(2CtL)≪1，因此可以近似认为Paidoussis方程是双曲型的。

对于双曲型偏微分方程，如果初始时刻在某区间存在扰动，则经过一段时间后扰动影响的区域由方程的两条特征线决定[6]，初始扰动区间发生变化时将特征线沿x轴平移即可，示意图如图2所示。

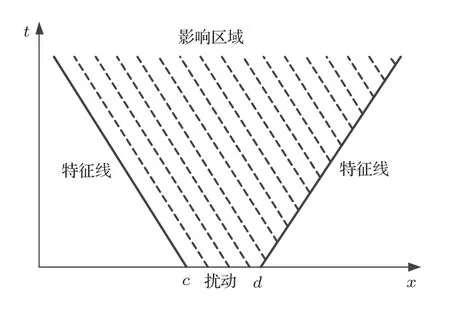
图2 扰动影响区域示意图Fig.2 Affected area of the disturbance

拖线阵运动过程中，拖船扰动的影响会由拖点逐渐传至缆尾，以拖船扰动时刻为初始时刻，将特征线沿x轴平移至与原点相交，则可用特征线表示阵上各点受到拖船扰动影响的时间。

3.1 近似拖直情况

计算拖线阵近似拖直情况下阵上各点对于拖船机动的响应时间，需要分别计算声阵段对于声阵段首端机动的响应时间以及拖缆段对于拖船机动的响应时间。

声阵段是零浮力缆，可直接利用Paidoussis 方程。式(2)的特征方程为

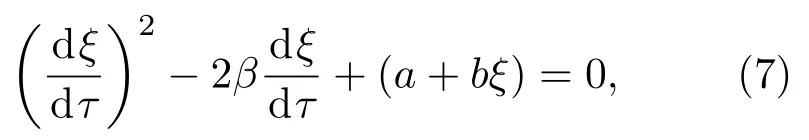
解此特征方程可得到描述特征线的微分方程如式(8)所示，由特征线即可得到声阵段上各点对声阵段首端机动的响应时间。

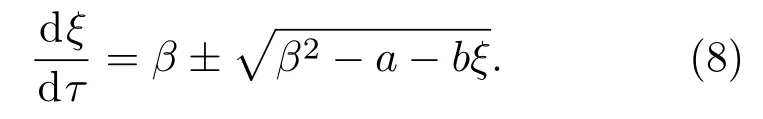
拖缆段密度通常大于水密度且拖缆段尾端并非自由状态，利用1.2 节方法将调整后的阻力系数以及形阻系数带入式(2)，进而求解特征线，可得到拖缆段对于拖点机动的响应时间。

3.2 阵形畸变情况

拖船停止转向开始直行时，拖线阵处于畸变状态，阵与流体在水平面内的夹角较大。而Paidoussis方程中表示微元段法向阻力的项(式(1)中最后一项)经过线性化近似，只适用于阵流夹角较小的情况，Rispin 通过实验证明阵流夹角大于3◦时线性化会带来较大误差[5]。因此，阵形畸变情况下拖线阵上各点对于拖船直行的响应时间，需要另行分析。

零浮力缆法向阻力表达式[7]为

其中，CDp是法向压差系数，Cf是法向摩擦系数，θ表示水平方向阵流夹角。Lopes 等[8]将微元段缆受力平衡方程从欧拉坐标系变换到拉格朗日坐标系，展开sinθ和θ发现二者小于2 阶的项相等，因此可将式(9)中的sinθ替换为θ。

以拖船停止转向开始直行时为初始时刻，用θ(x,t)表示阵上x位置在t时刻的阵流夹角。已知处于自由状态的缆尾端阵流夹角为0，拖线阵处于回转稳态时阵流夹角从拖点到缆尾逐渐减小，假设阵流夹角沿拖线阵线性变化，则初始时刻阵上各点的阵流夹角为

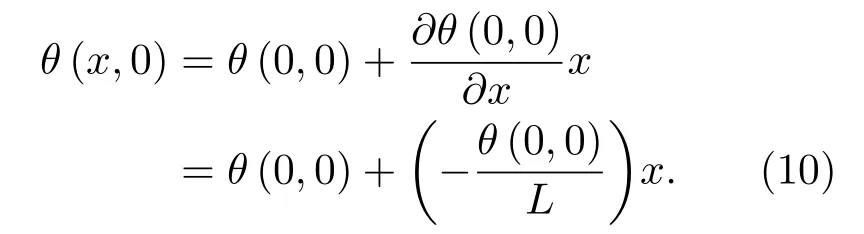
拖船停止转向开始直行后，假设阵上各点阵流夹角随时间线性减小，若初始时刻拖点处阵流夹角为θ0，利用全增量公式结合式(10)可得

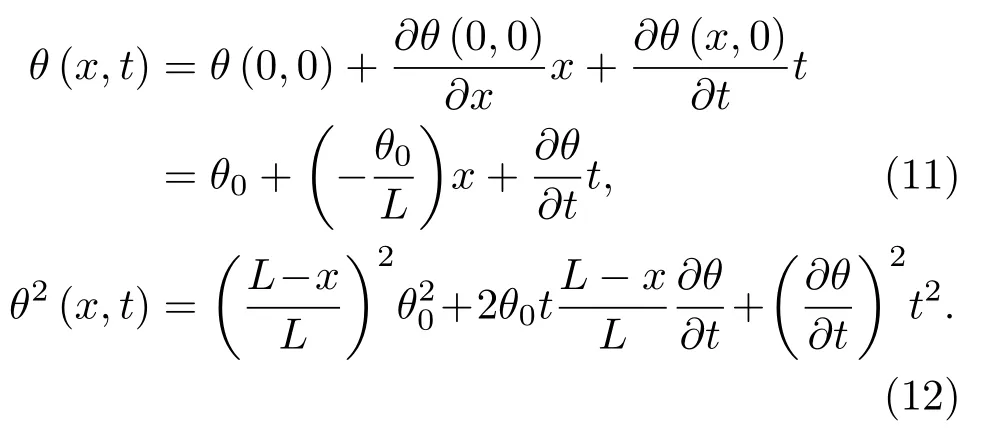
由于∂θ/∂t ≪1，且θ=∂y/∂x+U−1∂y/∂t[9]，式(12)可近似表示为

将式(11)和式(13)带入式(9)，进而用其替换式(1)中最后一项，可得处于回转稳态的缆在拖直过程中的运动方程，求其特征方程和特征线，即可得到声阵段对于声阵段首端直行的响应时间。

计算畸变的拖缆段对于拖船直行的响应时间时，拖缆段尾端非自由状态导致式(10)不成立，假设回转稳态的拖缆段尾端阵流夹角为θ1，应将初始时刻拖缆段上各点阵流夹角表示为式(14)，其中θ0和θ1可利用拖线阵回转稳态特性计算得到：

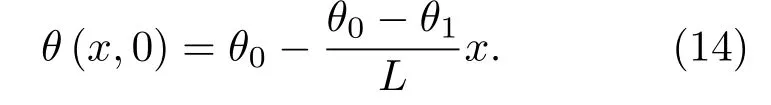
4 实时阵形估计方法

首先探究阵上各点过渡态时长的计算方法，以阵尾端为例，拖船转向机动过程中拖船和阵尾端航迹示意图如图3所示。拖船运动到B点时开始转向，在E点结束转向开始直行，尾端在A点脱离直行稳态，C点进入回转稳态，D点脱离回转稳态，F点进入直行稳态，拖船在E点结束转向时尾端位于H点，O点为圆心。拖船经过某点的时间用T加上标表示(如TB)，尾端经过某点的时间用T加下标表示(如TA)。

图3 拖船和阵尾端航迹示意图Fig.3 Track of tug and array end

设拖船转向角度∠BOE=φ，角速度为µ。以拖船开始转向的时刻为起始时刻，则TB= 0，TE=TH=φ/µ。

通过第3 节方法计算得到尾端对于拖船转向和直行的响应时间分别为tf和tl，则TA=tf，TD=TH+tl=φ/µ+tl。由于尾端在圆弧CD段角速度与拖船在圆弧BE段角速度相等，因此∠HOD=tlµ。

回转稳态时的拖线阵首尾相位差可用稳态振荡响应模型计算得到，设∠EOH=χ。尾端在回转稳态阶段转过的角度为

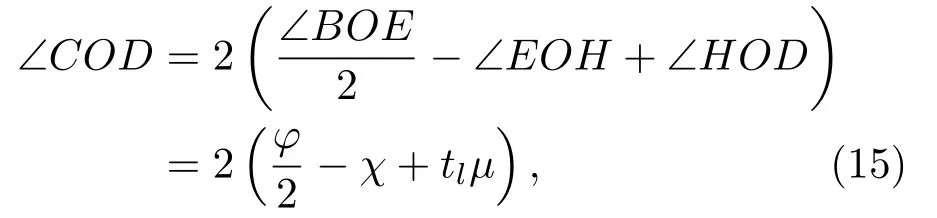
进而可得尾端在过渡段的时长

拖线阵处于直行稳态时阵上各点沿阵切线方向一致，处于回转稳态时阵上相邻两点沿阵方向的差值恒定，可利用稳态振荡响应模型计算得到。假设阵上相邻两点的沿阵方向差在过渡段线性变化，利用阵上各点在过渡段的时间以及回转稳态时的方向差，即可得到过渡段阵上相邻两点沿阵方向差的变化速率。根据之前假设，处于过渡态的相邻两点沿阵方向差增大和减小的速度相同。

因此，根据当前拖船运动状态和阵上各点对于拖船机动的响应时间，可判断阵上各点所处运动阶段。再利用沿阵方向差变化速度计算相邻两点沿阵方向差。最后假设阵上相邻两点之间缆呈直线，利用沿阵方向差和相邻两点间距递推计算阵上各点位置坐标，实现阵形的实时估计。

至此，可将阵形估计算法流程归结如下(流程图如图4所示)。第一步，根据拖船转弯半径和拖线阵物理属性，利用式(3)计算拖线阵的稳态回转阵形。第二步，利用式(8)计算阵上各点对于拖点转向和直行的响应时间。第三步，利用式(16)计算过渡段时长，结合稳态回转阵形，得到阵上相邻两点方向差在过渡段的变化速率。第四步，根据当前拖船运动状态，计算阵上相邻两点沿阵方向差，得到阵列位置坐标。由于避免了传统流体力学类阵形估计方法中雅克比矩阵求逆等步骤，因而所提方法具有更好的稳定性。

图4 阵形估计算法流程图Fig.4 Algorithm flowchart of array shape estimation

由式(16)可知，过渡段时间长度与拖船转向角度无关，因此阵上各点对拖船转向/直行的响应时间和沿阵方向差变化速度仅由拖船航速和转弯半径决定。对于转弯角度较小的情况，靠近阵尾端的点尚未进入回转稳态就受到拖船直行的影响向直行稳态过渡，可认为这些点受到拖船直行的影响后，沿阵方向差停止增大，并以相同的变化速度逐渐减小。

5 实验结果与分析

5.1 仿真验证

假设拖线阵中的拖缆段和声阵段均为光滑圆柱体，由Ansys R16.0 软件计算其阻力系数如表1所示。

表1 光滑圆柱体阻力系数Table1 Drag coefficients of smooth cylinder

Ablow 模型经过海试验证，具有一定的可靠性，可以将其计算结果作为真实值。采用表1、表2所示拖线阵参数，令拖船以一定转弯半径转过150◦，用Ablow 模型计算转向机动过程中的拖线阵阵形。将阵上某点的估计位置按时间顺序连接可得到此点航迹，进而可计算航迹的曲率。绘图显示拖点、全阵1/4位置、全阵1/2位置、全阵3/4位置、缆尾的航迹曲率，如图5所示。

表2 拖线阵参数Table2 Parameters of towed linear array

假设某点航迹的曲率小于5×10−5时，此点处于直行稳态，大于此点航迹曲率最大值的90%时处于回转稳态。依次计算阵上每个点脱离/进入直行稳态与达到圆弧顶点时间差的比值(图1中TAC/TCE)，并计算此点进入/脱离回转稳态与达到圆弧顶点时间差的比值(图1中TBC/TCD)，结果如图6所示。

图5 阵上若干点航迹的曲率Fig.5 Curvature of the track of several points on array

图6 各阶段起止时刻沿圆弧顶点比例Fig.6 Ratio of the start and end time of each stage to the apex

由图6可知，时间差比值基本上在1 附近，可以近似认为脱离/进入直行稳态和回转稳态的时刻关于圆弧顶点对称。

绘图显示拖船转向后以及拖船直行后阵上各点航迹曲率变化情况，并用第2 节所述方法分别计算拖线阵上各点对于拖船机动的响应时间理论值，结果如图7、图8所示，图中白色虚线为响应时间理论值。

由图7、图8分析可知，阵上各点受到拖船转向影响后航迹曲率逐渐增大，受到拖船直行影响后航迹曲率逐渐减小，特征线方法计算得到的拖线阵响应时间与Ablow 模型得到的航迹曲率开始变化的时间基本一致，表明第2节提出的方法较为有效。

拖线阵声呐通过波束形成得到目标相对于声阵段中心的舷角，而声呐最终输出的是目标相对于本船的方位角。需利用本船航向及估计的声阵段首尾阵元连线方向，将目标相对于声阵段的舷角转化为相对于本船的舷角，再转化为相对于本船的方位角。因此，估计阵形与真实阵形各自首尾阵元连线的法向之差，可以表示阵形估计误差造成的目标方位估计误差，示意图如图9所示。

图7 拖船转向后拖线阵航迹曲率变化情况Fig.7 Curvature change of the array after the tug turn

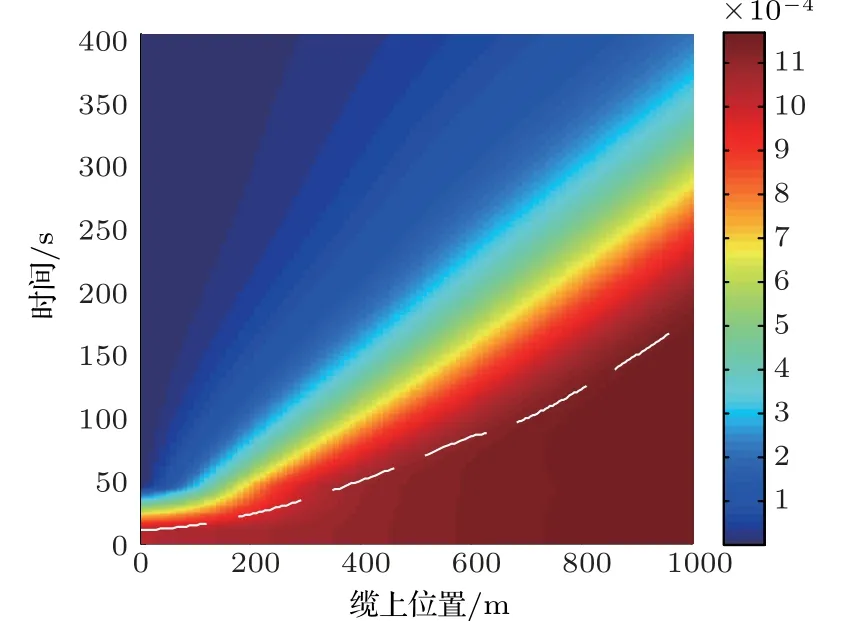
图8 拖船直行后拖线阵航迹曲率变化情况Fig.8 Curvature change of the array after the tug goes straight

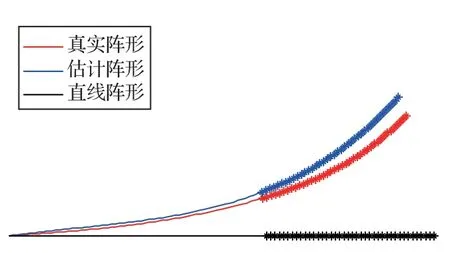
图9 方位估计误差示意图Fig.9 Schematic diagram of DOA error

采用表1、表2所示拖线阵参数，假设声阵段上均匀嵌入41 个阵元，拖船航速6 kn，令拖船以一定转弯半径转过120◦，以Ablow 模型计算结果为真实阵形，利用本文方法得到估计阵形。对于不同转弯半径的机动情况，相比于未校正阵形(直线阵)，计算阵形校正后阵列输出信噪比的增大和方位估计误差的减小，结果如图10所示。

图10 信噪比和方位估计误差的变化情况Fig.10 Changes of SNR and DOA error

由图10 可知，对于上述假设，当转弯半径在300 m～600 m 区间内时，利用本文方法校正阵形可使阵列输出信噪比增大约1.57 dB，方位估计误差减小约35.6◦。

5.2 海试数据运用

海试数据来源于2017年8月在我国东中国海海域实施的一次综合性水声试验，试验中拖船航速大约5.1 kn，全阵长1200 m，在130 s 时间内完成一次约30◦的转向机动。不做阵形校正以及用本文方法校正阵形后的方位历程图如图11、图12所示。

图11 不做阵形估计的方位历程图Fig.11 Bearing time record without array shape estimation

图12 用本文方法校正阵形的方位历程图Fig.12 Bearing time record using proposed method

图11 中不做阵形校正的左右舷方位历程图互为镜像，从中选取两个目标进行分析，目标1 的舷角从88◦变化到75◦，目标2 的舷角从146◦变化到125◦。由图12 分析可知，用本文方法进行阵形估计后，两个目标在右舷历程图上的轨线变得聚集且清晰，可以判断目标均位于右舷。以第360 s 为例，分析阵形校正前后目标信噪比的变化，此时刻右舷功率谱图如图13所示。

由图13 可知，通过阵形校正，可使目标1 和目标2 的输出信噪比分别提升约1.82 dB 和1.46 dB，说明估计阵形与真实阵形匹配较好，间接证明了本文所提算法的有效性和可行性。

图13 功率谱图Fig.13 Power spectrum

6 结论

本文分析了转向机动过程中拖线阵上各点的运动特性，探究拖线阵上相邻两点沿阵切线方向的变化规律，根据当前拖线阵上各点的运动状态计算相邻两点沿阵方向差，实现由局部到整体的阵形估计。计算机仿真和海上实验数据验证表明算法基本有效，与传统的流体力学类阵形估计方法相比具有更高的稳定性和更好的工程应用前景。