轨道板中超声兰姆波传播的有限元计算和实验∗

朱文发 孟翔震 张 辉 范国鹏 张海燕 张玉洁

(1 上海工程技术大学城市轨道交通学院 上海 201620)

(2 上海大学通信与信息工程学院 上海 200444)

0 引言

无砟轨道结构是高速铁路线路基础的主要结构形式，在环境气候条件与列车荷载的共同作用下，无砟轨道结构的劣化状态显著。据上海铁路局2017年的调查统计显示，沪杭高铁轨道板缺陷主要表现为脱空病害和表面裂缝[1]。轨道板缺陷已成为影响高速铁路行车速度和行车安全的主要危险源。然而，轨道板缺陷的检测目前仍然主要依赖工务人员在检修“天窗期”的巡视检查和手动探伤[2]，效率低。针对结构内部脱空问题的现代无损检测方法主要有电磁雷达法、远红外成像法、冲击回波法以及超声波法。电磁雷达法[3]受金属介质的影响大，而在轨道板中密布大量的钢筋和预应力筋严重影响电磁雷达的探测性能。远红外线成像法[4]的检测深度为10 cm之内，且需要在上午和傍晚检测(此时的气温变化最快)，而高铁的检修“天窗期”为夜间1点到4 点，在时间上制约了远红外成像法在轨道板缺陷检测上应用的可能性。冲击回波法[5]需要诱导板的自由振动，而无砟轨道质量较大，且受钢轨的约束，很难诱发轨道板的自由振动。超声波法[6]主要利用声阻抗的变化来判断结构内部是否存在缺陷，在理论上具有可行性。因此，获取实验数据研究超声波在轨道板中的传播规律对利用超声波检测轨道板缺陷至关重要。因此，本文利用具有大面积、长距离检测等优势的兰姆波检测方法，结合先进的非接触式空气耦合超声技术，分别通过有限元和实验研究了空气耦合条件下超声兰姆波在轨道板中的传播规律，为后续开展轨道板缺陷检测与成像的研究提供理论依据和实验方法。

1 轨道板中的兰姆波

轨道板是一种典型的混凝土结构，其材料参数如表1所示。检测时一般采用100 kHz 以下的低频超声波[7]，其波长比骨料尺寸大。因此，可以将轨道板视为均质材料。根据描述兰姆波的波动特性的瑞利-兰姆方程[8]

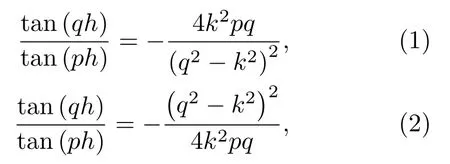
利用二分法、牛顿-拉菲逊等迭代算法，求解式(1)和式(2)可以得到轨道板中的声传播的兰姆波相速度和群速度频散曲线，如图1所示。

表1 轨道板的材料参数Table1 Material parameters of track slab

图1 轨道板中兰姆波的相速度和群速度Fig.1 The phase velocity and group velocity of Lamb wave in the track slab

在板中传播的兰姆波，若由频散曲线得到某一频率下的波数k2，则相速度为c2=ω/k2。因此，当使用空气耦合超声探头激励时，声束的入射角θ可以由Snell定律[9]得到：

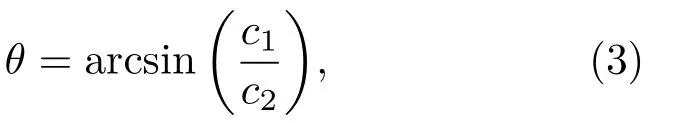
其中，c1为空气中的声速。

根据式(3)，可得到兰姆波的相速度频散曲线各模态的入射角-频厚积的频散曲线。如图2所示，当板厚一定时，入射声波的频率与入射角之间是一一对应的关系，当入射角为8.8◦、激励频率为50 kHz时，轨道板中A0模态的兰姆波趋于Rayleigh波。一般情况下，为保证接收到较强的兰姆波，要求接收探头的频率与角度和激励探头相同。

图2 入射角-频厚积的频散曲线Fig.2 Incident angle-f·d dispersion curve

2 有限元计算

由沪杭高铁嘉兴南站的轨道板理论计算结果可知，当频厚积很大时，A0 模态兰姆波将趋于Rayleigh波。而轨道板的厚度为200 mm，使用三维有限元计算量将相当大。因此，在声场分析专业软件PZFlex 上建立如图3所示的二维有限元模型进行模拟，其中z方向是板状结构的厚度方向，红色部分表示厚度为d的板状结构，绿色部分表示空气，空气中圆柱表示发射探头。有限元中的参数设置见表2。

图3 轨道板二维有限元模型Fig.3 Two-dimensional FE model of track plate

表2 二维有限元仿真模型的参数Table2 Parameters of two-dimensional FE simulation model

沿轨道板板厚和宽度中心以20 mm为步长，采集10 个点的数据如图4(a)所示。根据兰姆波的波包到达不同接收点的时间差，可以计算出兰姆波的群速度为2220 m/s，与Rayleigh 波的理论群速度2247 m/s 相吻合。在远离激励源的位置，在A、B 两点间，以5 mm为步长，沿轨道板板厚和宽度中心采集201组数据，并对采集到数据做二维傅里叶变换。如图4(b)所示，红线表示解析理论计算得到的f-k曲线，在50 kHz 的激发频率下二维傅里叶变换系数的较大值沿Rayleigh波的频散曲线分布。有限元计算结果与理论分析一致，频厚积较大时，A0 模态趋于Rayleigh波。

图4 有限元计算结果Fig.4 FE calculation results

3 现场测试

3.1 空气耦合超声波采集系统设计

开发了一套空气耦合超声波发射和接收系统，通过实验验证超声兰姆波在轨道板中的传播规律，从而为后续轨道板脱空缺陷检测提供方法。如图5所示，该系统主要由日本探头株式会社的JPR-600c 脉冲发生器、50 kHz 空气耦合超声探头、NI CDAQ9188XT 机箱、NI9775 模拟卡、NI9401 数字卡、具有带通滤波功能的前置放大器等组成，利用LabView 软件编写上位机程序控制超声传感器的激励和检测数据采集、处理的任务。

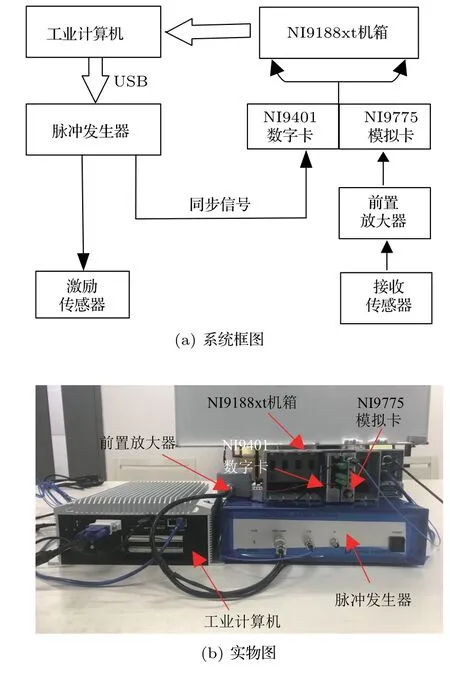
图5 空气耦合超声发射和接收系统Fig.5 Air-coupled ultrasonic transmitting and receiving system

3.2 测试位置

测试现场为沪杭高铁嘉兴南站CRTSII 型板式无砟轨道结构中如图6所示的标号为K82+977处服役的轨道板， 单块板尺寸为6450 mm×2550 mm×200 mm。使用中心频率为50 kHz 的空气耦合超声探头以同侧斜入射的方法激励和接收超声波，以一定的步长采集了不同位置的接收信号，分别计算了超声波传播的群速度以及利用二维傅里叶变换进行了模态识别。现场测试时实验系统的发射电压为550 V，数据采样率为2 Mbit/s。

图6 高铁现场测试现场Fig.6 Site test of high-speed rail

3.3 测试结果分析

利用中心频率为50 kHz 的空气耦合超声探头以8.8◦的倾斜角激励和接收超声波，接收到的实验信号及其频谱如图7所示。

固定发射探头，沿钢轨垂直方向，远离发射探头，以10 mm 为步进移动接收探头，每移动一次采集一组信号，共采集101 组实验信号。如图8(a)所示，求得该模态的群速度为2325 m/s，与Rayleigh波的理论值2247 m/s 相吻合。对不同接收点处的实验信号进行二维傅里叶变换，其结果如图8(b)所示。在50 kHz 的激发频率下，二维傅里叶变换系数的较大值，沿Rayleigh 波的频散曲线分布。实验结果表明在频厚积较大时，利用空气耦合超声激发的A0模态兰姆波趋于Rayleigh波，该结论与有限元计算结果和理论结果相同，为后续轨道板脱空缺陷的动态检测提供了实验方法。

图7 现场测试信号Fig.7 Test signal

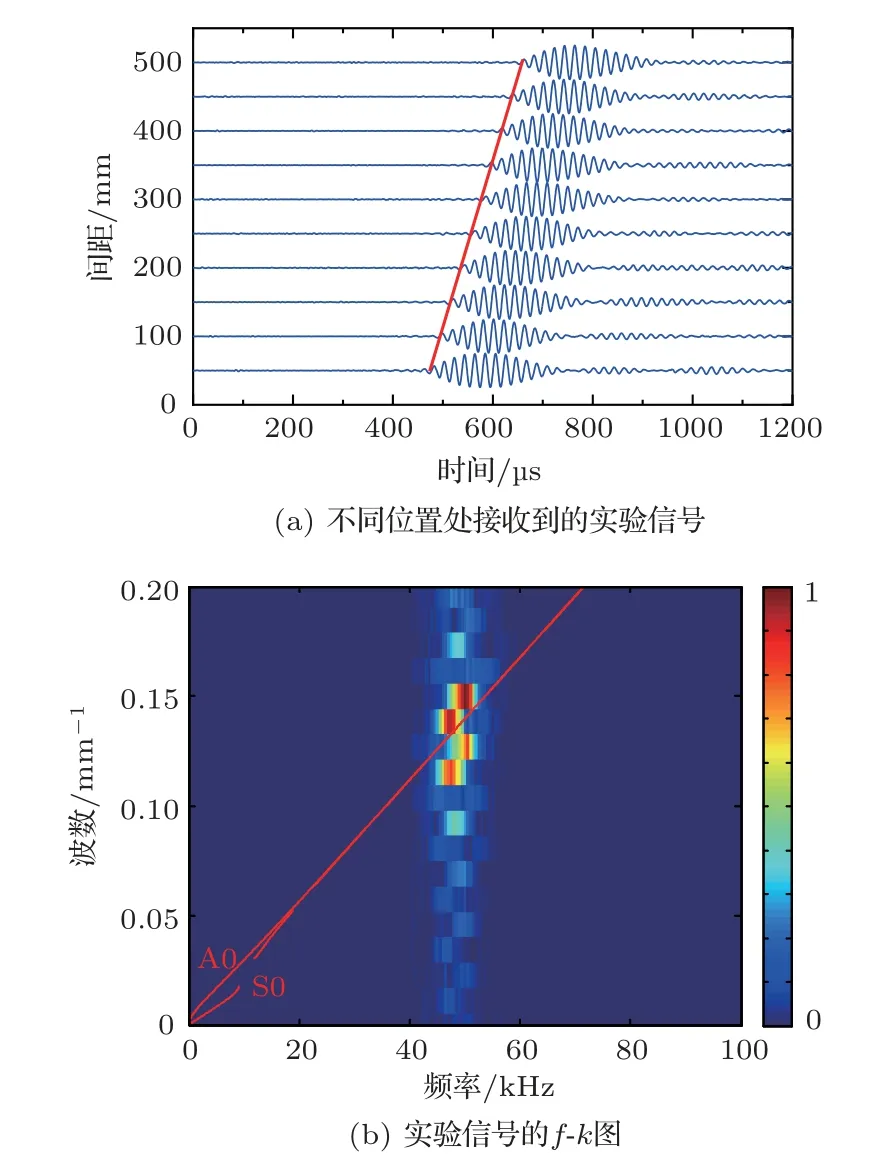
图8 实验结果Fig.8 Experimental results

4 结论

本文主要研究了超声兰姆波在高铁轨道板中的传播规律，主要结论如下：

(1)理论计算结果表明：利用空耦传感器斜入射轨道板可以激励出A0 模态，在频厚积为10 MHz·mm、入射角度为8.8◦时，激发出的A0模态趋于Rayleigh波。

(2)有限元计算结果表明：计算出兰姆波的群速度为2220 m/s，与Rayleigh 波的理论群速度2247 m/s 相吻合。在50 kHz 的激发频率下二维傅里叶变换系数的较大值沿Rayleigh 波的频散曲线分布。

(3)沪杭高铁嘉兴南站的现场测试结果表明：激发产生的兰姆波模态群速度为2325 m/s，与Rayleigh 波的理论值2247 m/s 相吻合。在50 kHz的激发频率下，二维傅里叶变换系数的较大值，沿Rayleigh波的频散曲线分布。

综上所述，有限元计算和现场实验结果表明：在大频厚积条件下，轨道板中传播的A0 模态兰姆波趋于了Rayleigh波。该特性可为轨道板表面及近表面缺陷检测的研究提供理论与实验方法。