声表面波在圆弧处反射及透射的数值研究∗

张 政 赵金峰 潘永东

(同济大学 上海 200092)

0 引言

激光超声技术[1−2]因其具有非接触、宽带、高灵敏度等优点，经过几十年的不断发展，现已逐渐成为无损检测领域的重要内容。弹性声表面波[3](Surface acoustic wave,SAW)的能量主要集中在材料表面附近传播，当遇到边缘时，同其他弹性波一样，会由于材料的不连续性发生散射、反射等现象。近年来，许多学者在材料表面引入不同尺寸规格的矩形凹痕，即通过构建缺陷边缘相对于表面呈90°：王余敬等[4]利用实验方法验证了材料表面的裂纹深度与反射回波两峰值对应的时间点差、透射波频谱的截止频率之间的关系；曹建树等[5]通过提取实验中表面缺陷回波特征信号，得到了管道表面缺陷的位置和深度。随着计算机技术的广泛应用，有限元方法凭借其在处理复杂几何模型与边界条件上的灵活性，可以更加精确地模拟脉冲激光激发出的超声波在介质中的传播。王明宇等[6]利用有限元软件研究了反射表面波的正向峰值和下一次正向位移所对应的时间的比值与裂痕深度之间的关系；关建飞等[7−10]通过数值模拟软件证明了反射回波信号和透射表面波信号与缺陷深度之间的联系；孙宏祥等[11]采用有限元技术，根据表面波信号的传播路径和到达时间，利用渡越时间法检测材料表面凹痕的深度。另外，又有学者改变了边缘相对于表面波传播方向的角度：Dutton 等[12]在材料表面引入不同深度的20°∼170°的V字形斜裂纹，验证了裂纹的角度及深度与表面波反射系数、透射系数之间的关系。以上的研究内容均是利用表面波在边缘处的传播性能，实现了对构件的健康检测。

然而，沿着材料表面传播的瑞利波遇到边缘时，其反射信号和透射信号不但与边缘相对于表面的角度有关，而且也与边缘相对于表面的拐角曲率半径有关。目前，关于在平面上传播的表面波遇到圆弧过渡面时，对其传播性能的影响尚无全面的科研成果发表；同时，对于一些工程构件在表面淬火时，硬化区与非硬化区之间存在着较大的切向或轴向拉力而形成过渡区裂纹，这种裂纹由过渡区向表面扩展而呈表面弧形裂纹。因此，开展声表面波在圆弧处传播性能的研究更加具有实际应用价值。

本文利用有限元方法模拟了热弹机制下，线性脉冲激光辐照金属铝板表面时激发的声表面波在近表面传播过程中，在圆弧过渡面处发生反射和透射的过程。首先，通过改变圆弧曲率半径以及激光脉冲上升时间，对平面上行进的表面波在圆弧过渡面处发生的声波反射现象以及透射现象进行数值分析，建立了圆弧半径与反射表面波以及透射表面波时域信号特征之间的联系。之后，在本文研究成果的基础之上，通过在构件上表面引入圆弧形凹痕，根据数值模拟软件计算结果，对比之前学者研究的矩形凹痕，发现当裂痕深度相同时，圆弧形裂痕与矩形裂痕对于表面波波形信号的响应有着显著的差异。分析结果为基于时域波形信号特征定量检测构件表面圆弧形缺陷深度提供了有效的理论基础，也进一步推动了激光超声无损检测领域的发展。

1 激光超声有限元理论及模型建立

1.1 热弹耦合理论

采用热弹机制激发超声波时，激光源的功率密度较低，会被材料迅速吸收进而转化为热能。在辐照期间，由于热能不能快速扩散，会在表层的附近形成很大的温度梯度，进而引起热膨胀并且产生切向应力，最终产生超声波。在超声波激发的过程中，存在着超声场和温度场的耦合作用，利用有限元方法能够有效求解这种多物理场耦合的问题，并且可以得到全场的数值解。对于均匀各项同性的线弹性固体材料而言，Achenbach[13]给出了热弹耦合控制方程：

其中，k代表热传导系数，T和T0分别代表材料的实际温度和环境温度，β代表热弹耦合系数，且有β= (3λ+2µ)α，α是线性膨胀系数，u代表材料内部不同时刻的位移向量，cv代表材料的比热容，λ和µ代表Lame 常数，ρ代表材料的密度。在超声波激发的过程中，存在着温度场与超声场耦合的作用，T0β∇·代表超声场对温度场的影响项，β∇T代表温度场对超声场的影响项。q代表单位体积在单位时间内吸收的热量，可以根据激光脉冲在时间和空间上的分布特征表示为

其中，xG是激光线源中心的横坐标，E0是线源单位长度上激光输出的脉冲能量，A(T)代表样品表面对入射激光的吸收率，RG是高斯型激光线源的半宽，t0代表激光脉冲的上升时间。

1.2 有限元模型的建立

本文采用ABAQUS 有限元软件中的Explicit显示器求解器求解瞬态的波传播问题。脉冲激光束的能量密度在空间上呈高斯分布，经过柱面透镜汇聚后，呈线状辐照到材料表面，激光线源沿y轴方向均匀分布，在光源长度范围内，材料承受的外力不随y轴变化，沿着y轴方向的应变和位移都是0，可以将三维瞬态弹性问题简化为二维平面应变的弹性模型来研究[14]，如图1所示。为了消除或者减少边界反射的影响，平面左侧和下侧均采用CINPE4 平面无限单元作为吸收边界[15]。在上表面距离右侧边界8 mm 的A 处施加激光源激发表面波，在距激光源右侧4 mm 的B 处(观测点Re2)左右1 mm 各自设置两个观测点Re1 与Re3。同理，在右侧边界距上表面4 mm 的C 处(观测点Re5)上下1 mm 各自设置两个观测点Re4与Re6。

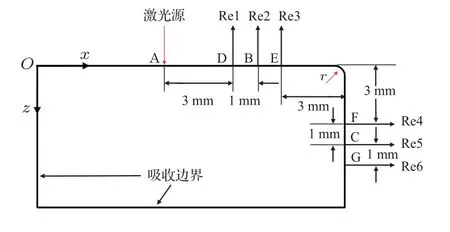
图1 激光激发与波接收的有限元模型Fig.1 Finite element model of laser generation and wave reception

表1 有限元模型中铝的材料参数Table1 Material parameters of aluminum for the finite element model

本文所选材料为金属铝，建模时其属性设置见表1(在模拟计算过程中，忽略了环境温度变化对材料参数的影响)。不同类型的声波在材料铝内的传播速度见表2，其中VS、VL、VR分别代表横波、纵波、表面波在铝内的传播速度。

表2 铝材料内部声波的传播速度Table2 Velocity of waves in aluminum material

在研究过程中，固定激光线源的半宽始终等于100 µm，仅仅改变激光脉冲上升的时间，以此来获得不同中心频率的声表面波。本文选取上升时间为10 ns，100 ns 作为实验对照数据，经过快速傅里叶变换之后，结果如图2所示。当上升时间为10 ns时，入射表面波中心频率约为6.71 MHz，对应的一个表面波中心波长在430 µm左右；当上升时间为100 ns时，入射表面波中心频率约为5.19 MHz，对应的一个表面波中心波长在560 µm左右。

图2 上升时间为10 ns 和100 ns 时入射表面波的频谱Fig.2 The incidence of SAW in frequency with the rising time of 10 ns and 100 ns

2 数值分析

取上升时间为10 ns，圆弧半径r= 0 µm，即边缘相对于表面的角度为90°。通过位移时差法：设Re1、Re2、Re3 之间的距离为∆l(∆l为1 mm)，信号通过相邻观测点之间的时间设为∆t,由式v= ∆l/∆t可以确定Re1、Re2、Re3 在不同时刻接收到的不同类型的声波信号。图3(a)展示了观测点Re2 处掠面纵波(P)、掠面横波(S)、直达表面波(R)、反射纵波(PP)、反射表面波(RR)出现的时刻；同时，入射超声波到达边缘时，根据惠更斯原理，拐点相当于一个次声源[16]会重新产生纵波和表面波，部分会直接回到接收点(即图3(a)中的纵波转化的表面波信号(PTR)和表面波转化的纵波信号(RTP))，部分会继续向下传播。这与文献[17]中的结果是一致的。同理，可以求得观测点Re5 处掠面纵波(P)、头波(H)、掠面横波(S)、透射表面波(TR)出现的时刻，如图3(b)所示，这也与文献[18]的结果吻合。

图3 位移波形图(r =0 µm)Fig.3 Displacement waveforms plots(r =0 µm)

反射表面波及透射表面波是需要重点研究的信号，在金磊等[17]、冯湾湾等[18]学者研究的基础之上(即r= 0 µm)，通过改变边缘相对于表面的拐角曲率半径，研究直达表面波在不同曲率半径的圆弧过渡面处发生反射及透射的过程。模拟圆弧半径由0 µm 增至2000 µm(步长值为100 µm)，截取位移波形图3(a)中t由3.5 µs增至4.5 µs，对反射表面波信号(观测点均为Re2)进行详细分析，结果如图4所示。

图4 观测点Re2 的位移波形图(r =0 µm–2000 µm)Fig.4 Displacement waveforms at observing point of Re2 (r =0 µm–2000 µm)

图5 观测点Re5 的位移波形图(r =0 µm–2000 µm)Fig.5 Displacement waveforms at observing point of Re5(r =0 µm–2000 µm)

当圆弧半径从0 µm 增至200 µm 时，直达表面波在圆弧过渡边界经过反射后，反射表面波的能量随着半径的增大而增大。当圆弧半径大于200 µm时，随着圆弧半径的增加，反射表面波回波信号的能量不断减小。同理，截取位移波形图3(b)中t由3.5 µs 增至4.5 µs，对透射表面波信号(观测点均为Re5)进行详细分析，结果如图5所示。当圆弧半径小于400 µm 时，透射表面波的能量是随着弧形曲率半径的增大而减小的，当圆弧半径大于500 µm时，透射表面波的能量是随着弧形曲率半径的增大而增大的。

将反射表面波与透射表面波的位移幅值和与其对应的圆弧半径大小分别绘制在图6(a)中。当圆弧半径r <0.5λ(λ代表一个表面波中心波长)时，反射表面波的能量是不断增大的；当r=0.5λ时，此时反射的表面波能量达到最大；当r > λ时，反射表面波的能量随着圆弧半径的增大不断减小，透射表面波的能量随着圆弧半径的增大不断增大，增长率逐渐减小，表明圆弧半径增大到某一数值时，表面波能够完全绕行，不再发生反射。但是反射表面波的能量最大值在r= 0.5λ处，透射表面波的能量最小值在r=λ处，即当反射表面波的能量最大时，此时透射表面波的能量并非最小。分析原因发现是表面波在圆弧处的部分反射是伴随着模式转换的，当r < λ时，圆弧仍然可以看作是一个奇异点。如模拟圆弧半径由200 µm 增至1000 µm (步长值为100 µm)，截取位移波形图3(a)中t由3.2 µs增至3.6 µs，对直达表面波转化为纵波(RTP)信号进行详细分析，如图7(a)所示；当圆弧半径0.5λλ时，反射表面波的能量随着圆弧半径的增大不断减小，透射表面波的能量随着圆弧半径的增大不断增大，两种情况所观察到的现象是一致的。

图8展示了圆弧半径分别取0 µm、200 µm、400 µm、600 µm、800 µm和1000 µm时，表面波(此时一个表面波中心波长在430 µm 左右)在圆弧处的位移图像。从图8中可以更加直观地看出，当圆弧半径小于一个表面波中心波长时，表面波在圆弧过渡面是以反射与模式转换为主；当圆弧半径大于一个中心表面波波长时，随着半径不断增大，反射回来的表面波能量不断减少，此时表面波在圆弧过渡面是以透射为主。

图6 观测点Re2 处的反射表面波与Re5 处的透射表面波位移幅值图Fig.6 The displacement of reflected and transmitted SAW at observing point of Re2 and Re5

图7 观测点Re2 处的RTP 位移波形图Fig.7 RTP displacement waveforms at observing point of Re2

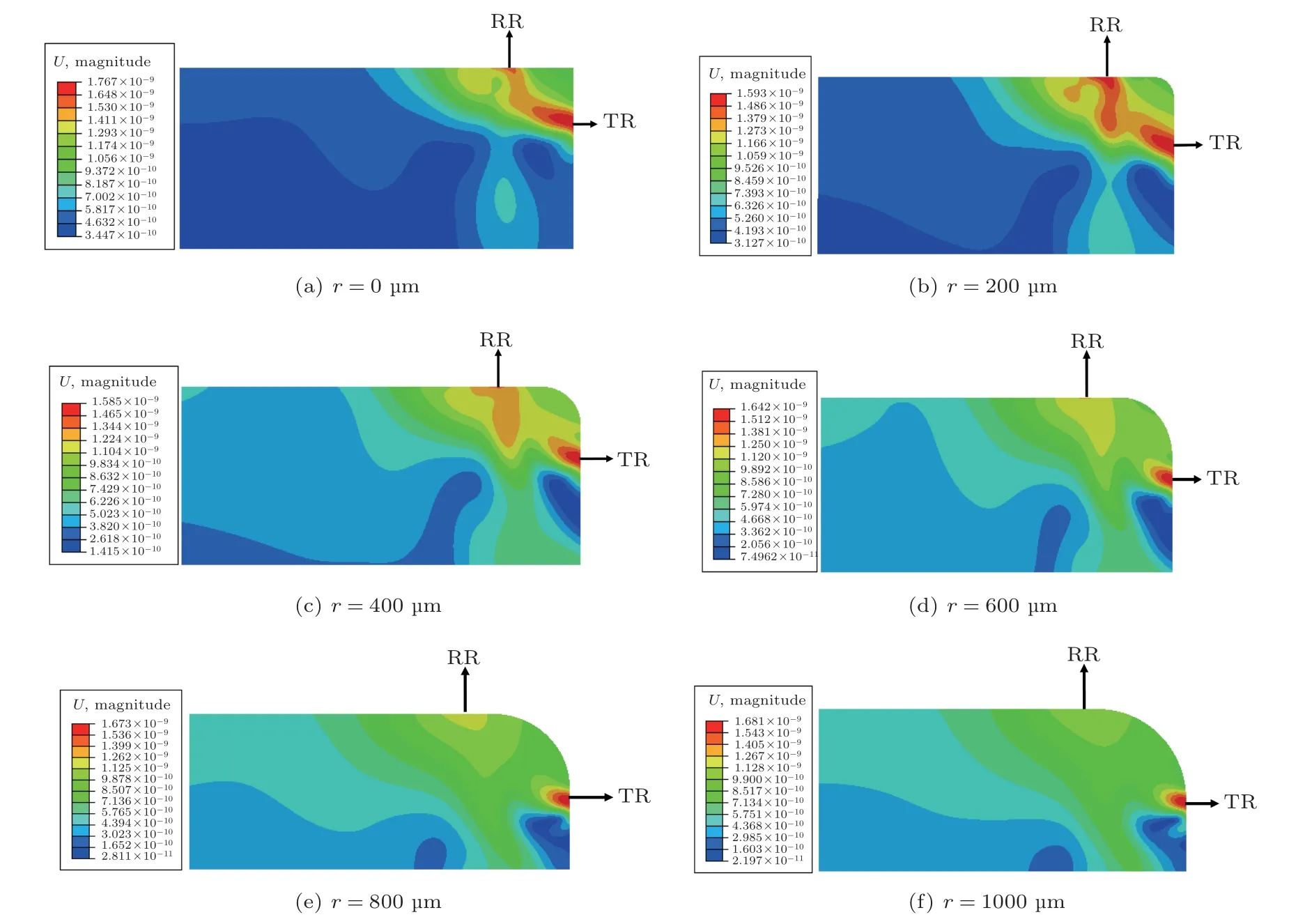
图8 圆弧过渡面处的声场图(t=3 µs)Fig.8 Sound field at the transition surface of the circular arcs(t=3 µs)

下面模拟研究激光激发声表面波和表面圆弧凹痕作用后产生的反射波场和透射波场。在上表面引入半径为r的圆弧形凹痕缺陷，激光激发点距离左侧边界11 mm，分别在凹痕左右两侧4 mm 和1 mm 处设置两个观测点Re7与Re8。平面左侧、右侧和下侧均采用CINPE4 平面无限单元作为吸收边界，以消除声波到达边界时发生反射对原有波形信号造成干扰，如图9(a)所示。

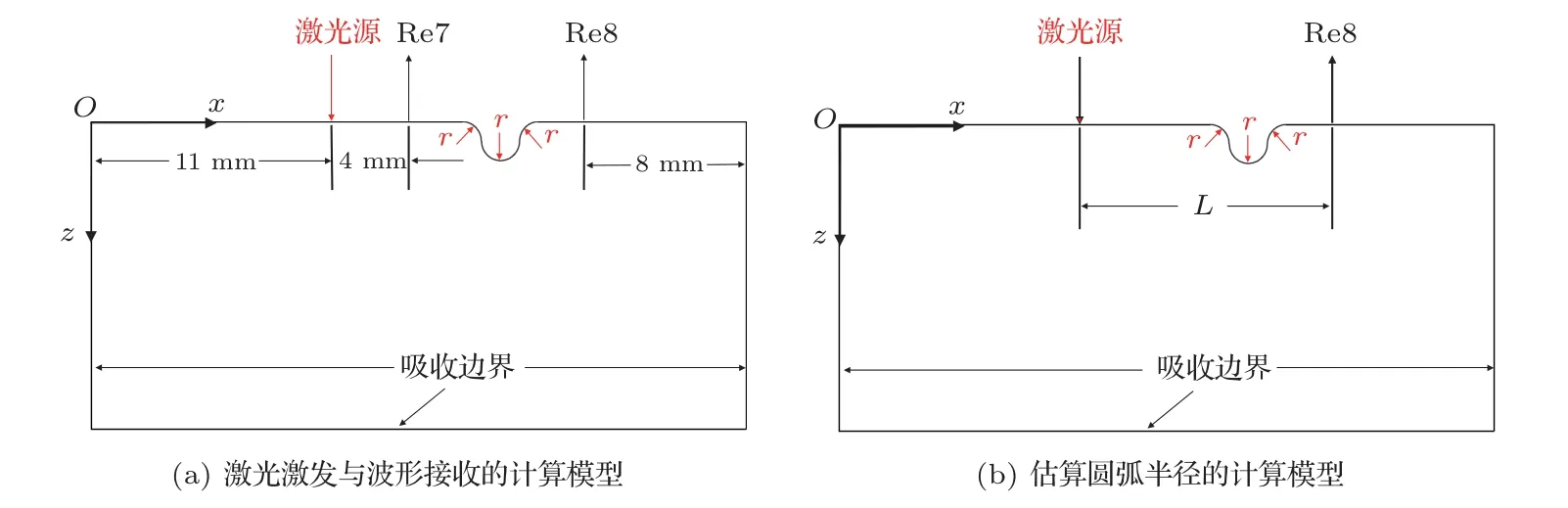
图9 含有圆弧形缺陷与激光激发表面波作用的有限元模型Fig.9 Finite element model of the interaction of the LESAW with the arc defect

图10 反射表面波和透射表面波信号Fig.10 The signal of reflected and transmitted Rayleigh wave

取激光脉冲上升时间为10 ns，圆弧半径等于400µm。图10(a)与图10(b)分别展示了观测点Re7接收到的掠面纵波(P)、掠面横波(S)、直达表面波(P)和反射表面波(RR)出现的时刻；以及观测点Re8接收到的透射纵波(TL)、透射横波(TS)和透射表面波(TR)出现的时刻。通过改变圆弧半径的大小，对观测点Re7 接收到的反射表面波信号与Re8接收到的透射表面波信号进行详细分析。发现当r <0.5λ时，随着圆弧半径的增加，反射表面波的能量是不断增大的；当r >λ时，随着圆弧半径的增加，反射表面波的能量是不断减少的，如图10(c)所示，说明此时表面波是以透射为主的，这一结论与前文的研究结果是一致的。

若将激光源与观测点Re8 的水平距离设为L，如图9(b)所示。根据透射表面波出现的时刻t，估算圆弧凹痕的半径r′：

式(6)中，L(单位：mm)代表从激光源处至观测点Re8的水平距离，t(单位：µs)代表透射表面波的到达时间，r′(单位：mm)代表圆弧的估算半径，v(单位：km/s)代表表面波在材料中的传播速度。

将圆弧实际半径和估算半径之间的相对误差(|r −r′|/r)与圆弧实际半径的拟合结果绘制在图10(d)中。发现当r < λ时，二者之间的相对误差较大，考虑原因是此时直达表面波在圆弧过渡面处会发生反射和波形转化的现象，情况相比于曲率半径大于一个表面波中心波长时要复杂得多；当r > λ时，实际值与估算值之间的相对误差控制在2%以内，说明此时直达表面波在圆弧过渡面处是以透射为主的。这与文献[9]中提及到的利用反射表面波信号与透射表面波信号定量检测表面矩形裂纹深度的结论恰恰相反。原因在于声表面波的能量主要集中于表面以下一至两个波长量级深度范围内，随着矩形裂纹深度(h)增加，表面波被裂痕阻挡发生反射的能量逐渐增多，而绕过裂痕继续向前传播的能量逐渐减少；但是对于圆弧形凹痕而言，随着圆弧半径的增大，即裂痕深度(h=2r)越深，反射回去的表面波能量越少，沿着凹痕绕行而过的表面波能量越多。因此，对于较深裂痕的情形，根据透射表面波信号到达的时间，利用公式(6)可以实现对弧形缺陷形状和大小较为精确的测量。这也说明了利用表面波在边缘处的传播性能对材料进行健康检测时，圆弧形凹痕和矩形凹痕在检测方法上存在的区别。

3 结论与展望

本文通过改变激光脉冲的上升时间，根据有限元建模仿真计算获得了中心波长分别为430 µm 和560 µm 两组表面波。首先利用两组数值实验研究了表面波在圆弧处的反射现象。仿真计算分析发现即当圆弧半径小于一个表面波中心波长的时候，表面波主要以反射与模式转化为主；当圆弧半径约为二分之一表面波中心波长时，反射表面波的能量最大。然后又研究了表面波在圆弧处的透射现象。计算分析发现即当圆弧半径大于一个表面波中心波长时，随着圆弧半径的增加，反射表面波的能量不断减小，透射表面波的能量不断增大；并且透射表面波位移幅值的增长率逐渐减小，表明当曲率半径增加到某一数值时，表面波将能够完全通过圆弧过渡面。

利用声表面波在圆弧过渡面处的传播性能与曲率半径之间的关系，模拟了激光激发声表面波与材料表面圆弧形凹痕的相互作用，并与之前学者研究的表面波与矩形凹痕的作用机理进行了对比。结果表明：圆弧形裂痕和矩形裂痕对于直达表面波的响应存在明显的区别。当裂痕深度较深时(裂痕深度大于两个声表面波的波长)，对于矩形缺陷而言，绕行而过的透射表面波能量很微弱；对于圆弧形缺陷而言，随着裂痕深度增加，绕行而过的表面波能量越来越多，根据透射表面波的到达时间反演裂痕深度大小，其估算值与实际值之间的相对误差在2%以内。这一结论为利用透射表面波时域信号估算圆弧半径的大小奠定了理论基础，也为表面含有弧形凹痕构件的健康检测提供了理论依据，更加促进了激光超声无损检测领域的进步。

后续将利用激光超声场检测仪对含有不同曲率半径圆弧凹痕的铝块进行激光超声实验，通过对采集到的超声波信号进行数据分析来验证数值计算的结果，相应的工作仍在进行当中。