高阶线性递推数列通项公式的研究

梁国俊

（广东江门中医药职业学院文化基础系，广东江门529000）

高阶线性递推数列是组合数学的重要内容，求通项公式是解高阶线性递推数列的关键，常用的解题方法多种多样，主要有：特征方程法[1]、矩阵法、迭代法、导数法、生成函数法和“齐次通解+特解”法[2]等等，其求解过程复杂，必须每道题都要根据题目的已知系数值来求解通项公式，并且，其系数要求是特定的值，否则便无法求解[3]。而所求出的通项公式均属于数值解的通项公式，只适用于原题的计算。对于任意常系数的高阶线性递推数列公式解的通项公式，国内外未见有文献报道。如:已知数列｛an｝中，a0、a1、a2、a3、a4、a5、a6、a7，从第 8 项起（n≥8 且 n∈z，A、B、C、D、E、F、G、H、k、b、d、f、g、h 均为任意常数），求通项表达公式 an。原有的各种方法就不能求解此题，因此，突破原有的解题方法，探索高阶线性递推数列公式解的通项公式具有非常重要的理论意义和实用意义。

1 研究策略

1.1 以递推数列关系式为依据

原有的解题方法中，均是以题目的系数值为依据来求解的，故求出的通项公式均是数值解的通项公式，只适用于原题的计算[4]。为探索公式解的通项公式，在研究探索过程中，是以递推数列关系式为依据，其系数均为任意常数而不是采用具体数值。

1.2 使用简易的数学符号和运算法

为便于计算，提高解题效率，使用简易的数学符号和运算法，既可用于计算机的编程计算，也可以适用于笔算解题。

1.3 有明确的通项表达公式，可直接计算an的值

原有方法中，还可用逐项累计法推算an的值，也可利用计算机编程来求解，但对于任意常系数的高阶线性递推数列，则只能求出各项的an值，而不能求出明确的通项表达公式。因此，需有明确的公式解的通项表达公式，才能适用于各阶各项的计算，以达到一式通解的目的。当代入题目的已知数和n的值时，便可直接计算出an项的值。

1.4 避免采用解高次方程的传统方法

原有的解题方法中，多是采用特征方程法或变换后再利用特征方程法，但高次方程难解，如出现超越方程就更难解，会直接影响通项公式的求解，甚至是无法求出通项公式，因此，必须突破原有的解题方法，避免出现解高次方程。

1.5 通项公式适用于各阶齐次与非齐次的高阶线性递推数列

原有方法中，生成函数法或“齐次通解+特解”法等虽能求解非齐次的线性递推数列的通项公式，但均属于数值解，只适用于特定系数的原题计算。因此，需以各阶的非齐次线性递推数列的关系式为依据，进行探索研究，寻求出其公式解的通项公式，才能适用于任意常系数的各阶齐次或与非齐次的高阶线性递推数列的计算。

2 公式推导与结果

参考一阶齐次线性递推数列，并对各阶非齐次线性递推数列进行逐项展开，寻找其变化规律，从而总结归纳出通项公式。

2.1 一阶非齐次线性递推数列

已知 a1，且 an=qan-1+k×bn+f×n2+g×n（n≥2 且 n∈z，q、k、b、f、g 均为常数），展开得

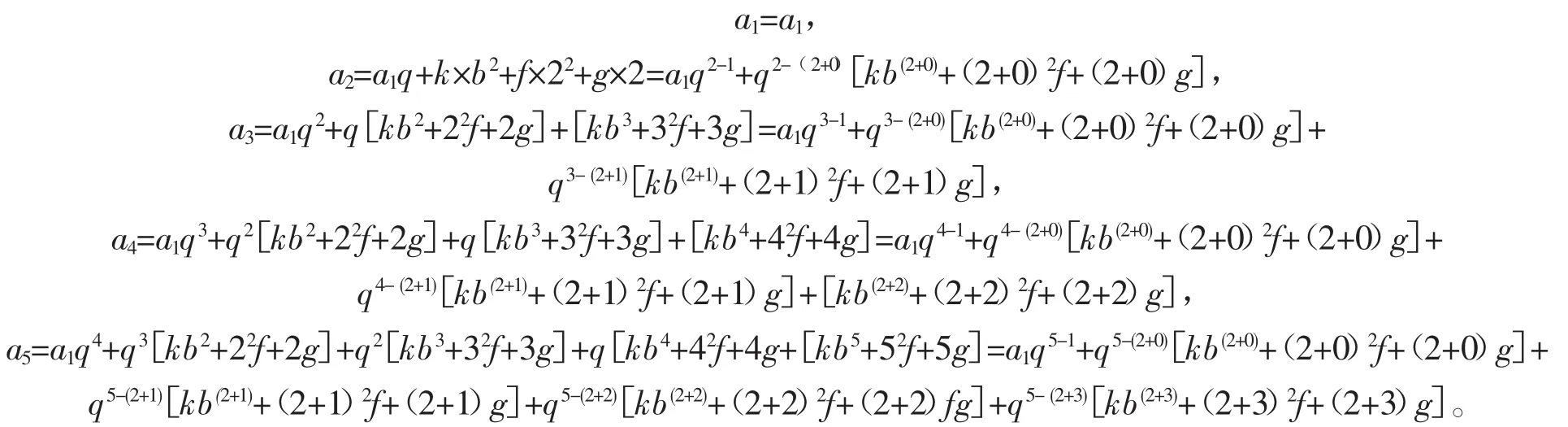
从中可发现其规律，并利用累加符号表示，归纳得出上述情形从第1项起的一阶非齐次线性递推数列通项公式为

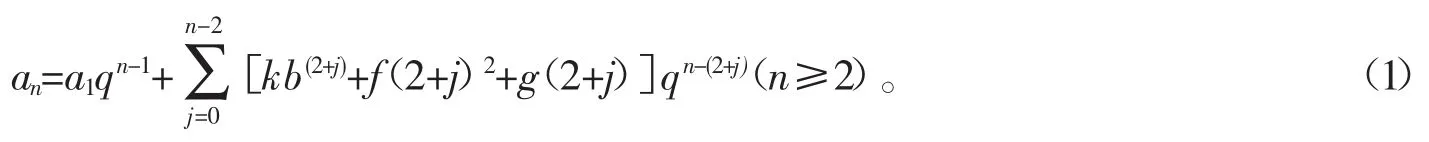
2.2 二阶非齐次线性递推数列

已知 a1、a2，且 an=Aan-1+Ban-2+k×bn+f×n2+g×n（式中 n≥3 且 n∈z，A、B、k、b、f、g 均为常数），展开得

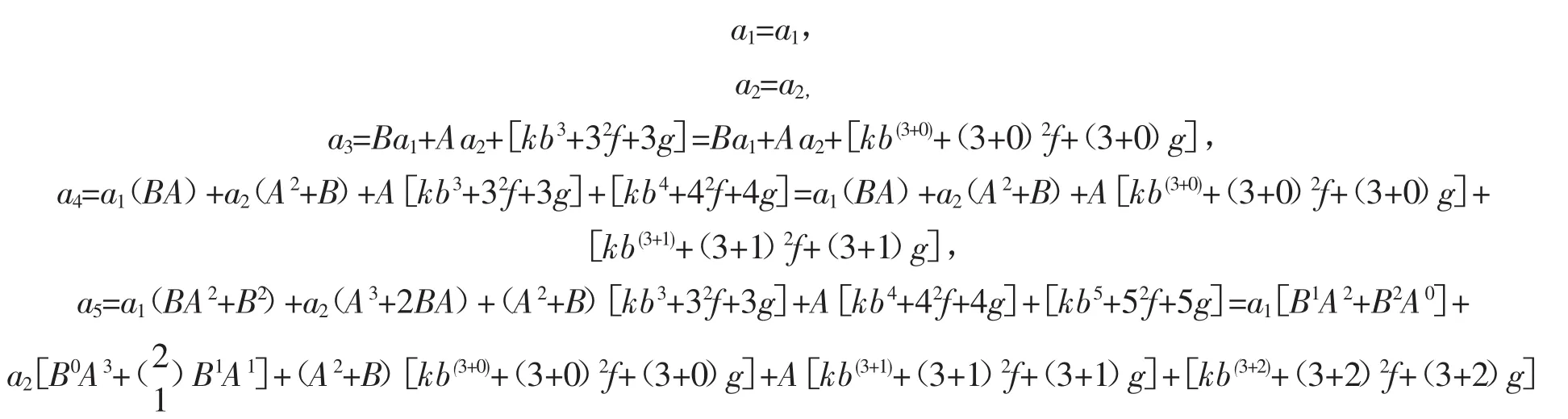
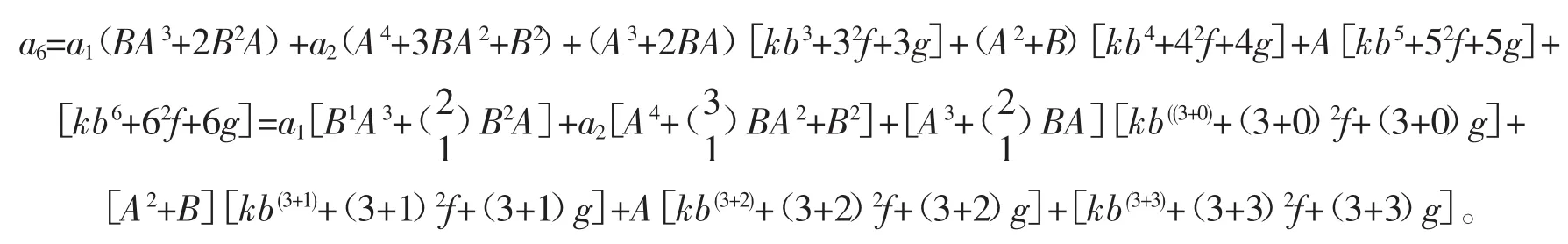
根据其规律性并参照一阶的通项公式的形式，可归纳出上述情形从第1项起的二阶非齐次线性递推数列的通项公式为

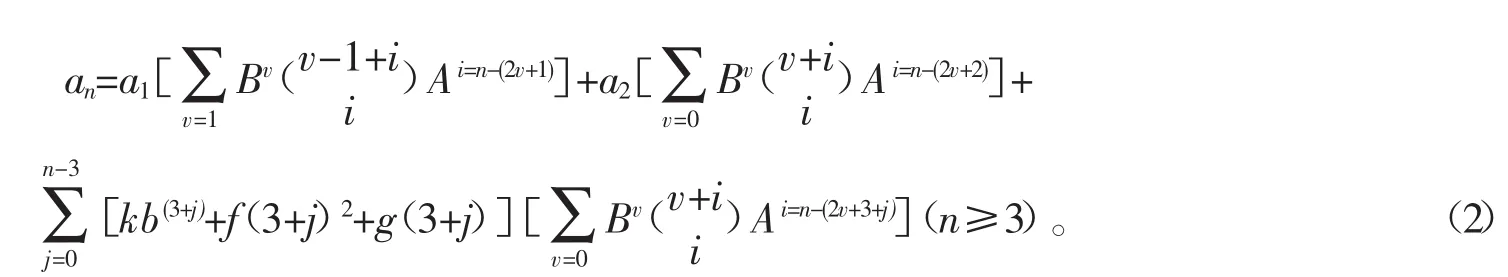
2.3 三阶非齐次线性递推数列

已知 a1、a2、a3，且 an=Aan-1+Ban-2+Can-3+k×bn+f×n2+g×n（式中 n≥4 且 n∈z，A、B、C、k、b、f、g 均为常数），展开得

根据其规律性并参照二阶的通项公式的形式，可归纳出上述情形从第1项起的三阶非齐次线性递推数列的通项公式为

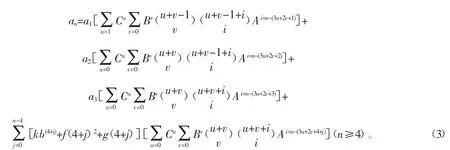
以此类推。

2.4 推导结果

根据前面各阶线性递推数列展开的规律性，并参照其通项公式的形式，归纳得出：

从W项起的M阶（M≤8）非齐次线性递推数列，形如：an=Aan-1+Ban-2+Can-3+Dan-4+Ean-5+Fan-6+Gan-7+Han-8+ψ（n）（式中 n≥W+M），其公式解的通项公式为

2.5 公式证明

已知 a1、a2、a3、a4、a5、a6、a7、a8、a9，且从第 10 项起 an=Aan-1+Ban-2+Can-3+Dan-4+Ean-5+Fan-6+Gan-7+Han-8+k×bn+f×n2+g×n（ 式中 n ≥10 且 n∈z，A、B、C、D、E、F、G、H、k、b、f、g均为常数），对照上式（4），本例是从第2 项起的八阶线性递推数列（W=2，M=8），ψ（n）=k×bn+f×n2+g×n，并代入式（4）得

用数学归纳法证明如下：

当 n=10时，代入式（5）得

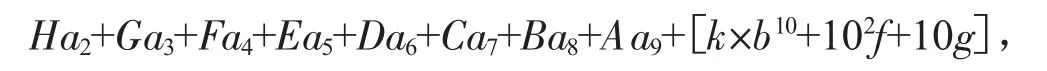
与原例的递推关系a10的展开式相等，所以等式成立。

当 n=11时，代入式（5）得

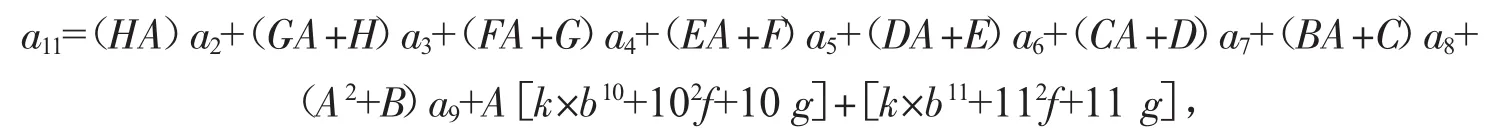
与原例的递推关系a11的展开式相等，所以等式成立。

当 n=16时，代入式（5）得

与原例的递推关系a16的展开式相等，所以等式成立。

当 n=17时，代入式（5）得

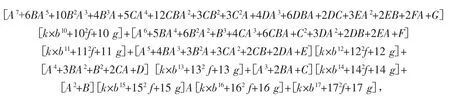
与原例的递推关系a17的展开式相等，所以等式成立。

假设 n=k（k≥10）时，代入式（5）成立，即有

当 n=k+1（k≥10）时，代入式（5）得

因为用n=k+1代入式（5）时，其右边的关系式与用n=k时右边的关系式的形式是相同的，所以n=k+1也成立。

因为式（5）成立，即式（4）成立。证毕。

3 例题与公式应用

例1已知数列｛an｝中，a1=a2=2，a3=a4=1，a5=a6=3，a7=a8=4，从第 9 项起 an=an-1+an-3-3an-5+5an-8，求通项表达公式an。

解本例是从第 1项起的八阶齐次线性递推数列（M=8，W=1），没有 B、D、F、G 项（即 v=0，t=0，x=0，y=0），A=1，C=1，E=-3，H=5，且 ψ（n）=0，代入式（4）得本题数值解的通项公式为

分别用n=9、10、11、12代入上式，便可计算出相应各项的值为

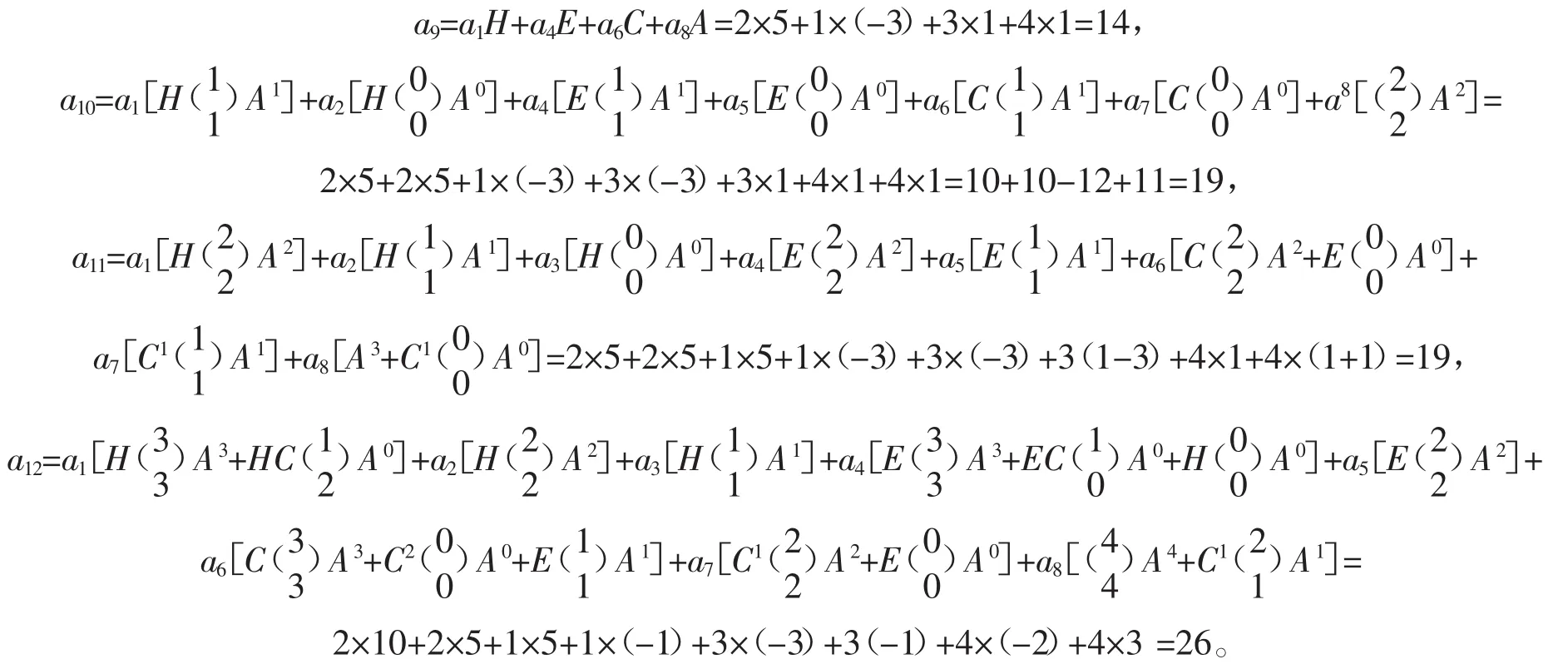
例2已知数列｛an｝中，a0=2，a1=1，a2=1，a3=0，a4=2，a5=0，a6=2，a7=1 且 an=an-1+an-3-3an-7+7an-8+2×3(n-5)+n2-7n+11（n≥8 且 n∈z），求通项表达公式 an。

解本例是从第0项起的八阶非齐次线性递推数列（W=0，M=8），没有B、D、E、F项（即v=0、t=0、r=0、x=0），A=1、C=1、G=-3、H=7，且 ψ（n）=2×3(n-5)+n2-7n+11，代入式（4）得本题数值解的通项公式为

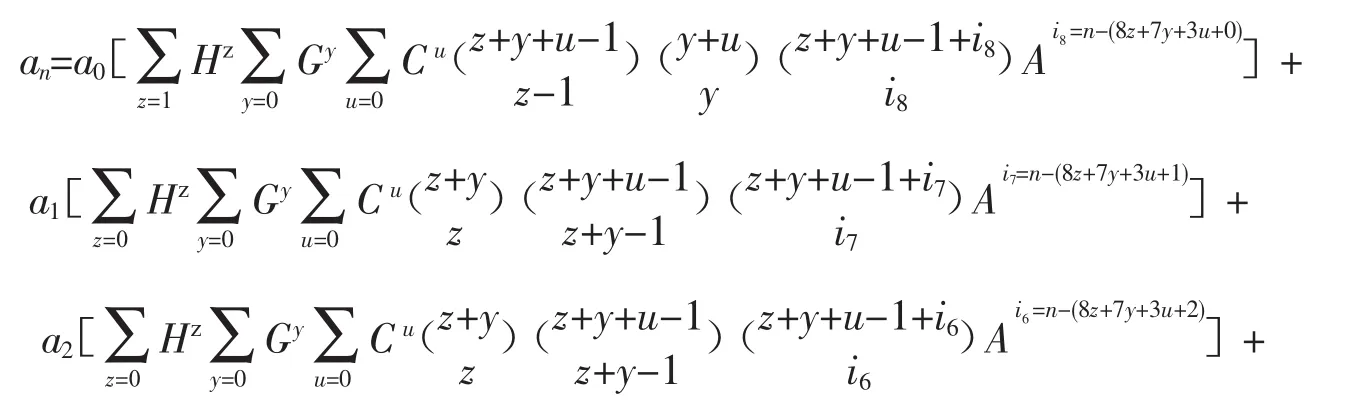
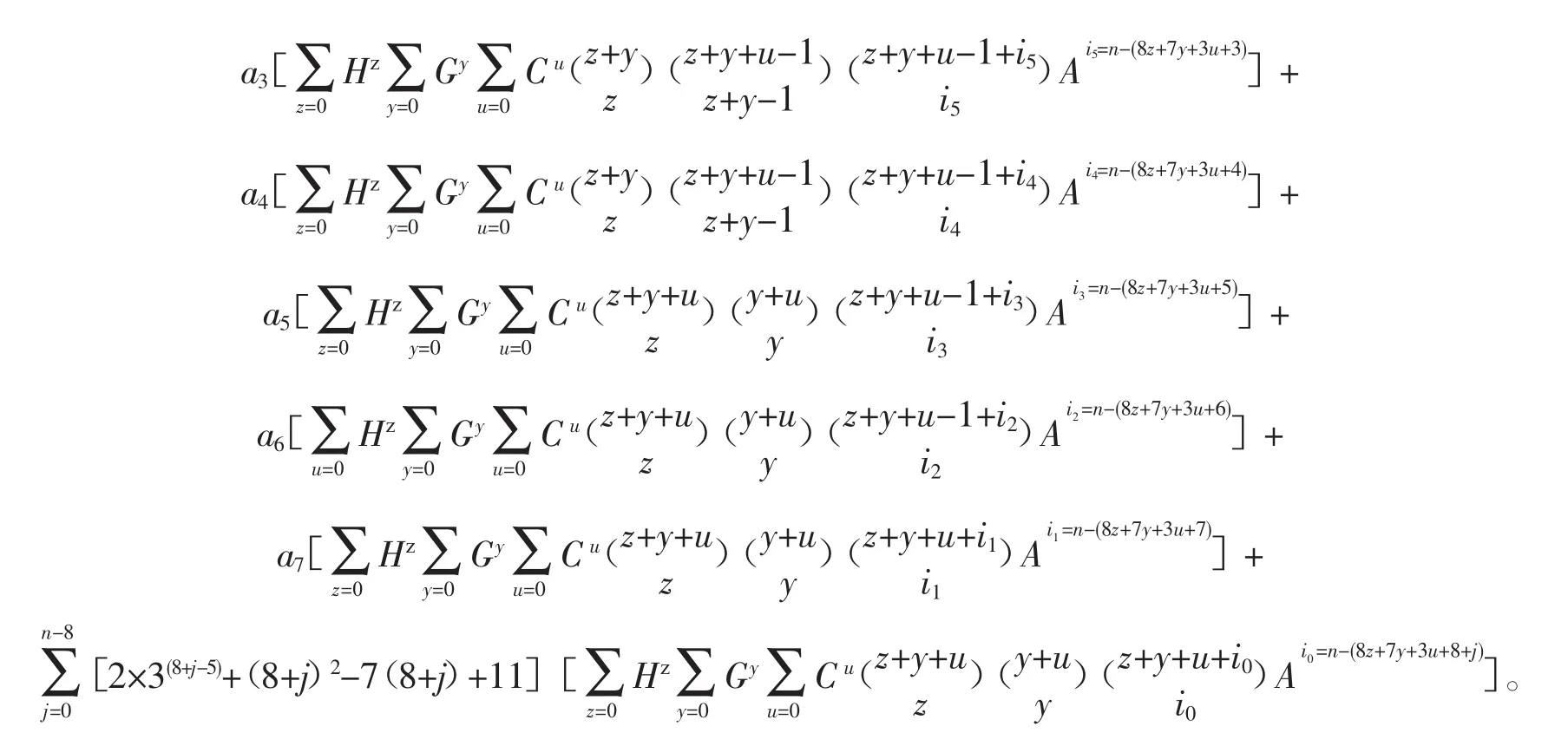
分别用n=8、9、10、11代入上式，便可计算出相应各项的值为

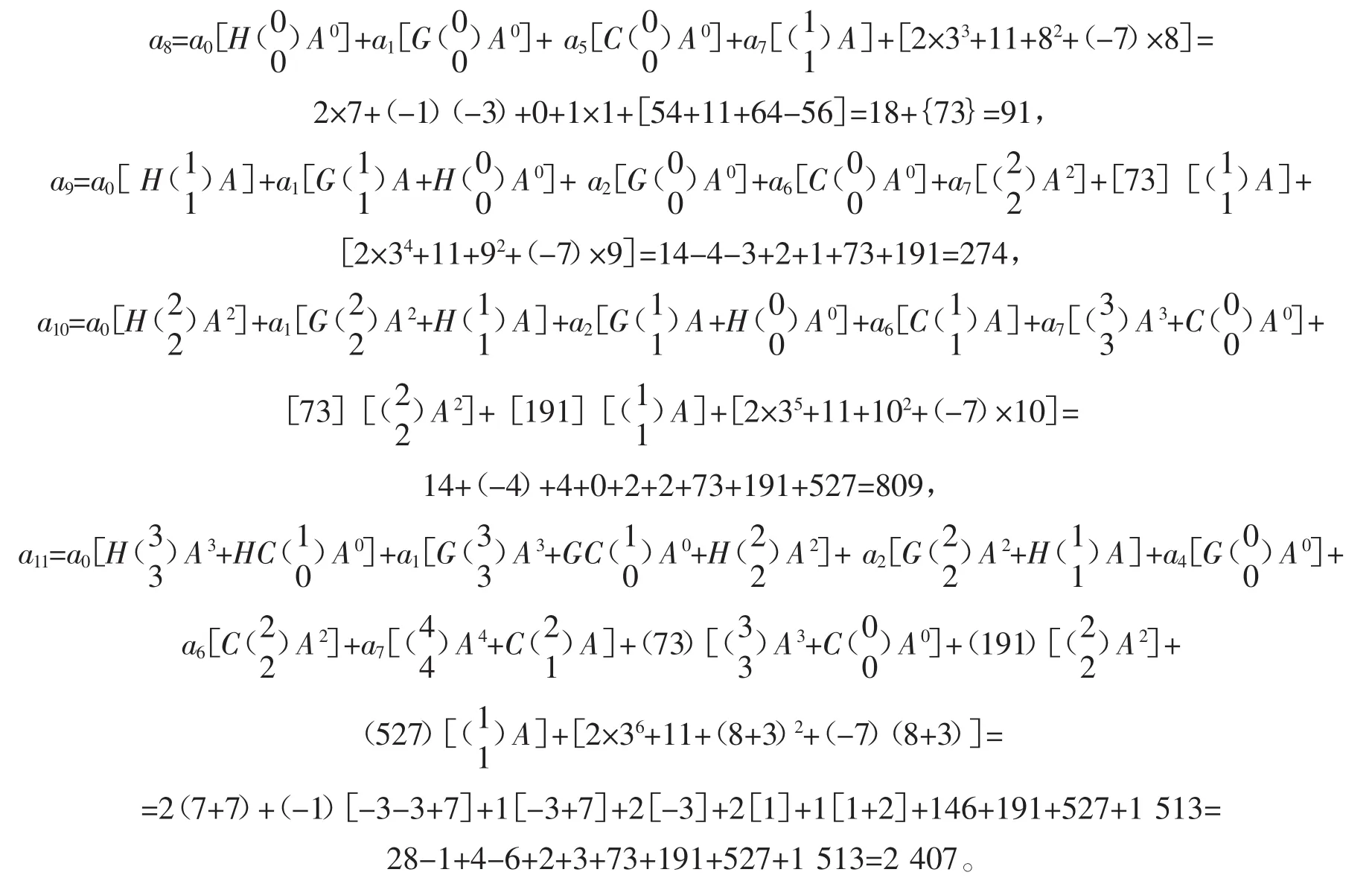
例3已知数列｛an｝中，a0=5，a1=2且an=an-1+6an-2+3n（n≥2且n∈z），求通项表达公式an。

解本题是从第0项起的二阶非齐次线性递推数列（W=0，M=2），对照式（4），没有H、G、F、E、D和C 项（即 z=y=x=r=t=u=0），并将 A=1、B=6、ψ（n）=3n代入通项公式（4）得本题数值解的通项公式为

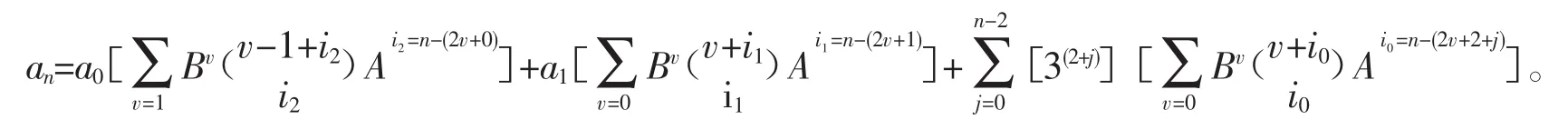
分别用n=2、3、4代入上式，便可计算出相应各项的值为

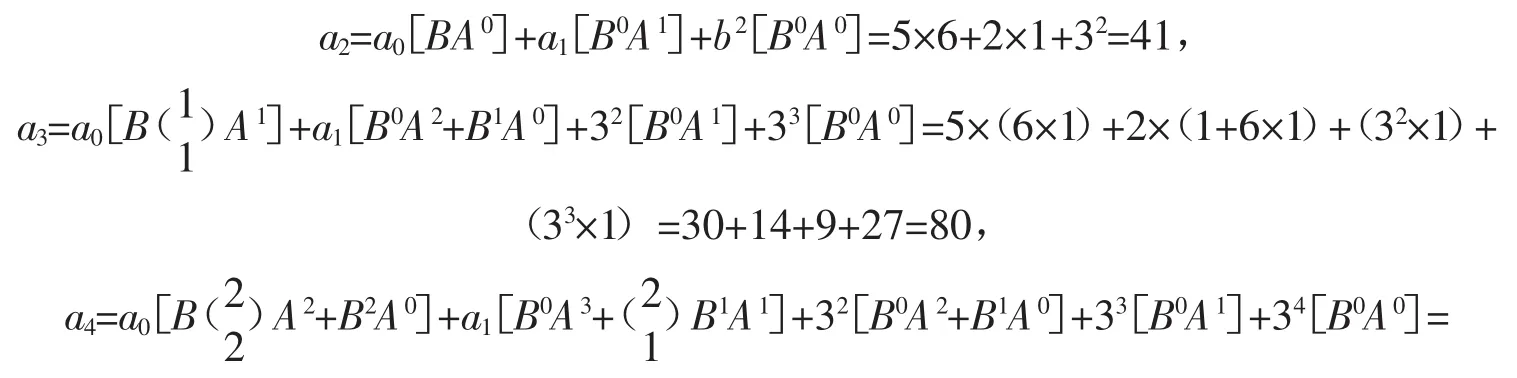
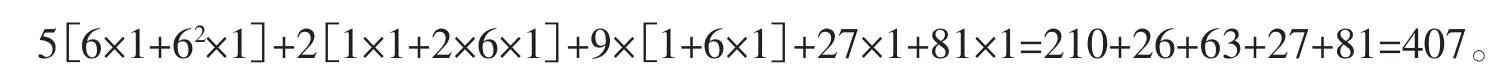
例4在数列｛an｝中，a0=-1，a1=1，a2=0，a3=2，a4=1，从第 5 项起（式中n≥5且n∈z），求通项表达公式an。

解本例是从第 1项起的四阶非齐次线性递推数列（W=1，M=4），B=C=1，D=-3，没有 E、F、G、H 项，即 r=x=y=z=0，同时没有 A 项，即，代入上述式（4）得本题数值解的通项公式为

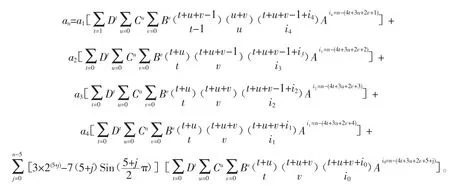
分别用n=5、6、7、8代入上式，便可计算出相应各项的值为

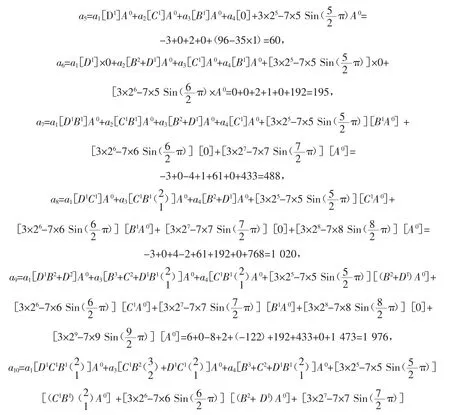
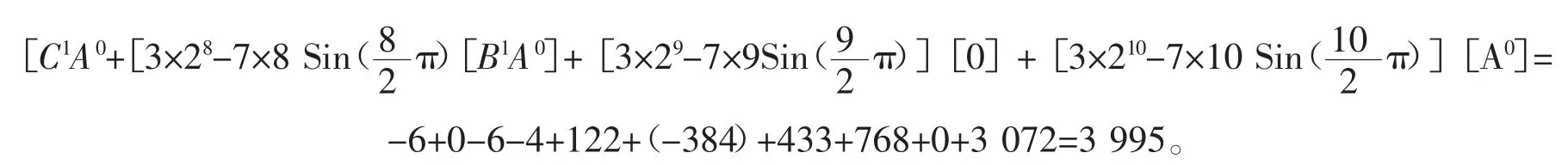
例5斐波那契数列，已知｛an｝中，a1=1，a2=1，从第3项起an=an-1+an-2（n≥3且n∈z），求an的通项表达式。

解本题是从第1项起的二阶递推数列，即 W=1，M=2，对照式（4），没有H、G、F、E、D、C项，即 z=y=x=r=t=u=0，A=1，B=1，且 ψ（n）=0，n≥3，代入通项公式（4）得本题数值解的通项公式为

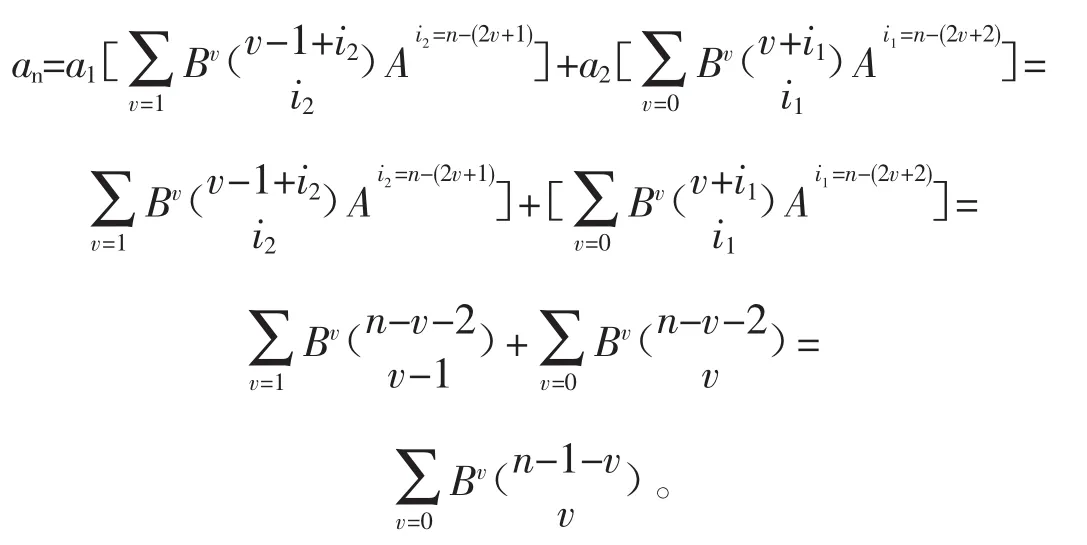
分别用n=3、4、5、6代入上式，便可计算出相应各项的值为

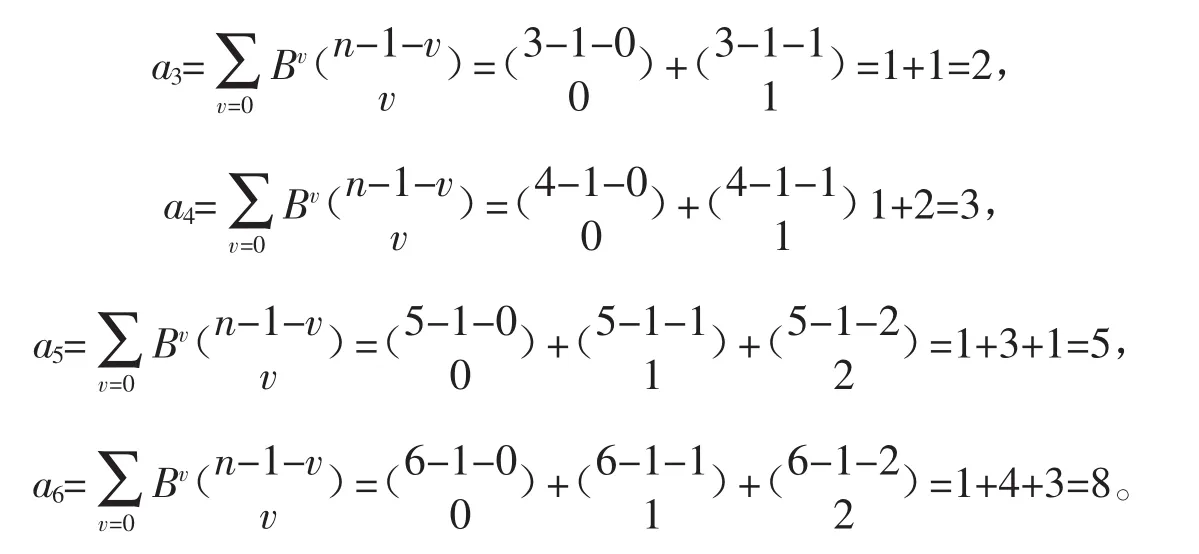
4 结论

本文通过逐阶逐项展开推导，找出其变化规律，归纳得出了一条高阶线性递推数列公式解的通项公式，该通项公式表达简单，算法简易，计算结果正确，且能通解任意常系数的八阶之内各阶线性递推数列，达到了快速求解的效果。用本通项公式计算与传统方法比较，有如下优点：

（1）容易掌握，适用范围广。适用于任意常系数的各阶线性递推数列，使用的符号和运算方法简单。

（2）有明确的通项表达公式，一式通用。是公式解的通项公式，适用于八阶以内的各阶任意常系数高阶齐次或非齐次线性递推数列的计算。

（3）可直接计算第n项的值an，还可以根据题目中的已知条件，求解初始项中各项的值或关系式中g（n）中的系数。

（4）不需解高次方程。避免解高次方程出现的无理根、复数根等难解现象。

（5）不存在“特解”的假设判断问题和难解现象。

（6）根据其规律性，还可扩展到九阶、十阶、…等的高阶线性递推数列的计算。

经过对高阶线性递推数列通项公式的研究，得出一条公式解的通项公式，能通解任意常系数的高阶线性递推数列。但公式解的通项公式较长，参数较多，难以记忆，计算时容易漏项。