“对比”与“体验”为数学课堂插上翅膀——“面积”与“面积单位”教学实践与思考

刘丹丹（特级教师）

【教学内容】

人教版三年级。

【教学过程】

一、创设情境，在“对比”中导入新课

1.“对比”中辨析周长不同。

师：同学们喜欢玩拼图游戏吗？这两个拼图有什么不同点？

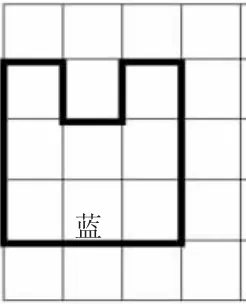
图1

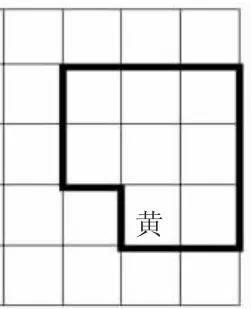
图2

生：这两个图形缺的一块小正方形的位置不同。

生：这两个图形面积不同。

师：你怎么知道？“面积”我们还没有学过呀，说说想法？

生：因为这两个图形缺少的边不同，所以……（学生沉思）

师：看来旧知与我们要学的新知混淆在一起了，那我们就从容易迷惑的地方开始新知学习吧。以前我们学过这样的知识，围成图1一周的长叫……（生：周长），围成图2一周的长叫（生：周长）。它们周长相同吗？（生：不同）

师：怎么看出来的？

生：图1缺的部分是3条边，图2缺的部分是2条边。

生：我是“移”边来比较的。

师：“移”再加个字就是……（生：“平移”）我们就用这个方法试试。

课件动态呈现平移过程：

图1

图2

师：对比平移前后图形周长的变化，看出不同了吗？

生：图1凹下去的那段，平移上去，就成了大正方形，图1周长比大正方形多了两条短边。图2平移两条边后就与大正方形周长相等。这样，图1周长就多出两条边，所以它的周长比图2长。

2.“冲突”中揭示本课题。

师：图1、图2有什么相同点？

生：图1和图2都比大正方形少了一块小正方形。

师：都用了几块小正方形拼的？（生：8块）都用了8块，我们就说这两个拼图的面积相等。

小结：这两个拼图的周长不同，但是它们面积相同。今天我们就来学习与面积有关的知识。（揭题并板书：面积和面积单位）

二、借助直观，在“体验”中认识新知

1.“体验”——观察与触摸中认识“面积”。

师：请看拼图，图1中蓝色图形的大小就是蓝色图形的面积，图2中黄色图形的大小就是黄色图形的——（生：面积）。

师：（用手摸向课桌面）课桌面的大小就是……（生：课桌面的面积）。（又用手指向黑板）谁来模仿说一下？

生：黑板面的大小就是黑板面的面积。

师：好了，我听见有人说，天花板面的大小就是天花板的面积，课桌面的面积比天花板的面积怎么样？（生：小很多）

师：接下来，请大家摸一摸数学书封面的面积，再请大家摸一摸数学书侧面的面积。谁来说一下它们之间……

生：数学书封面的面积比侧面面积大。

师：归纳一下，在你的想象中，什么是面积？

生：物体表面部分的大小就是面积。

师：物体的表面或者（指向投影上的拼图）封闭图形的大小，就是它们的面积。

2.“体验”——比较与探究中认识“面积单位”。

（1）谁的野餐垫大？

（出示一张学生春游照片）

师：记得春游那天老师问过大家“谁的野餐垫大呀？”你们有结果吗？

师：我选了两个野餐垫，（屏幕出示）两个都是长方形。

师：刚才比较课桌面与天花板面的大小时，同学们几乎异口同声地说出结果，现在怎么不说话了？为什么？

生：一个图形宽些，另一个图形长些。不好比较。

师：刚才比较课桌面与天花板面时，你们是怎么比出结果的？

生：刚才我们把课桌面“叠”到上面天花板上比的。

师：他用了一个“叠”字，实际上我们叠了吗？没有，我们是“看出来的”，这叫什么？（生：观察）课桌面与天花板面面积相差很大，我们用观察法就看出结果，可是这里图3和图4面积相近，我们用眼睛很难看出结果。怎么办？用你们说的重叠法来试试。

师：比出结果了吗？

生：没有。第一个图形宽多出一些，第二个图形长多出一些，没法比。

师：我们用观察法、重叠法都不能比较出面积大小，怎么办？

（让学生独立思考后，说一说想法）

生：可以把图上多出来的部分再来比。

师：多出来的部分用剪刀剪下来比？如果野餐垫是你的，你同意吗？

生：可以把多出的部分折叠着来比。

师：如果材质太硬不能折叠怎么办？

生：我把这两个长方形画在纸上，剪下来比。

师：借助中介物比较也是办法。

生：我们可以在背面画出相同的小方格来比。

师：同学们办法真多！这时“小精灵”等不及了，她告诉我们一个秘密：可以选用一种“小图形面”作单位来测量。

借助小精灵告诉的方法，分别用圆片、正三角形和小正方形来测量。课件动态呈现三种情况。

●第一种：圆形

师：小红身边正好有许多小圆片，她这样测量：

师：长的方向摆了几块？（生：5）宽的方向摆了几块？（生：2）一共摆了几块？（生：10）需要一块块数吗？［生：不用，5×2=10（块）］这个办法好！继续摆第二个图：

生：长里摆4块，宽里摆3块，一共 4×3=12（块）。

师：比出结果了吗？（生：比出来了，蓝色图形大）看来，摆圆片帮我们解决了谁面积大的问题。

●第二种：三角形

师：小军带来了许多小正三角形，他怎样用小正三角形来解决面积大小的问题呢？

生：红色图形，长摆9块，宽摆 2块，一共 9×2=18（块）。

生：蓝色图形，长摆7块，宽摆 3块，一共 7×3=21（块）。

师：用小正三角形测量能比出面积大小吗？

生：能，蓝色图形面积大。

●第三种：正方形

师：小青带来了小正方形，她说，我跟你们都不同，我用小正方形来测量。

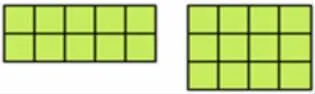
生：红色图形，长摆5块，宽摆 2块，一共 5×2=10（块）。

生：蓝色图形，长摆4块，宽摆 3块，一共 4×3=12（块）。

生：比出来了，还是蓝色图形面积比红色图形面积大。

（2）什么“图形面”作面积单位最合适？

师：三位同学都用自己的办法解决了问题，但用什么图形面作面积单位更合适？为什么？

生：用小正方形作面积单位最合适，因为用它拼没有空隙。

师：没有空隙地拼在数学上叫密铺。用圆片或小三角形拼都会有空隙，它只能大致帮我们比较面积的大小。所以要精确地测量面积要用什么小图形面作单位？

生：用小正方形作面积单位。

（3）在“体验”中认识常用的面积单位：平方厘米、平方分米、平方米。

（逐步出示1平方厘米、1平方分米、1平方米的正方形纸质模型并引导表述：什么是1平方厘米、1平方分米和1平方米）

介绍面积单位的写法。

找一找：找出身边哪些物体面积的大小大约是1平方厘米、1平方分米或1平方米。如：指甲盖的面积大约是1（ ）；1张小光盘正面的面积大约是1（ ）。

试一试：教师用报纸做了一个1平方米野餐垫，贴在黑板上。

师：如果这是一个野餐垫，可以坐几个人？（生：3个、5个）我在讲台边摆了一个1平方米野餐垫，请4个同学去坐坐。

师：如果是1平方米地面，可以站几个人？

（大约可以站15个学生）

三、操作实践，在“感悟”中内化知识

1.合作测量卡片面积。

（同桌合作测量一张卡片如图5或图6）

师：请选用合适的面积单位去密铺测量。哪个图形面积大？

图5

图6

（1）比较与选择。

师：你选用什么面积单位去测量？

生：平方分米。

师：请仔细观察图形上标的数据，投影上是放大的长方形和正方形，它们与实际大小有偏差。

学生经历周折，得出用平方厘米去测量最合适。教师拿出实际卡片让学生测量。

（2）操作与探究。

同桌合作测量，用1平方厘米学具，在卡片纸上密铺度量（每人只准备了8个1平方厘米的正方形，同桌2人共有16个）

师：有同学遇到麻烦了，小正方形不够用怎么办？

启发思考：一定要全部铺满，才能得出面积数吗？

生：小正方形数不够，只能在长铺10块，宽铺4块，这样能得出面积数。

2.闯关练习：课本第62页做一做。试一试再反馈。

下面图形的面积各是多少？

（）个□；（）个□； （）个□

3.实践作业。

（1）选用自制的合适面积单位测量课桌面的大小。

（2）一张扑克牌的正面面积有多大？（先估估，再用面积单位量）

【教学反思】

本节课是一次为青年教师上的“裸课”，整节课开场和展开部分与我预设一致，只有一处学生的表现出乎我的意料：就在合作测量环节——选用合适的面积单位测量时，学生竟然与我“背道而驰”，原来是投影放大惹的祸——学生选用黑板上实际的面积单位去对比测量放大的图形，这是我预设的不足呀，如果提前出示实际卡片会使课堂更有效。虽然有此处“意外”，但“体验式”学习仍使本课在以下三方面特点鲜明：

一、问题冲突点燃思维火花

本节课有三处问题冲突：第一，课始处，学生的回答表现出对“周长”和“面积”认识混淆。由于上学期学生已经建立了“周长”的概念，这里学生产生负迁移也是正常现象，本课教学时抓住新旧知识的“认知冲突”，在与旧知“周长”的“对比”中引入“面积”概念，便于学生厘清两概念的本质区别。同时由拼图方块导入面积相关知识的学习既直观又契合学生好奇的心理，也便于新旧知识的连接。第二，课中，选用什么“图形面”作面积单位来测量这个问题，学生充分交流之后，引入“小精灵”来告知小秘密，利用多媒体课件动态展示三位学生的不同方法，丰富了学生的选择背景，拓展了学生的思维空间。第三，课尾处，合作测量卡片的面积，学生经历选择合适面积单位的波折，再到拼摆不够的困难，直到找出解决问题的办法。这些“问题冲突”的解决促进了学生思维的发展和应用能力的提升。

二、直观操作激发学习兴趣

在生活中学生熟悉长度的测量，但学生由一维到二维的认识拓展遇到瓶颈，加上生活中人们大都是基于长度的测量通过计算得出面积的，因此学生对“面的测量”更加缺乏现实经验参照，这也是造成以往学生对面积大小估计困难的客观原因。解决的关键，在于给学生提供充足的“面的测量”机会，以弥补生活经验的缺失。本课中选用合适的“小图形面”测量面积——从观（课件）测量，到选用合适的面积单位测量——再到合作测量，为学生提供了较多的“面的测量”机会，培养了数感，满足学生在玩中学的心理需求。

三、数学思想方法提升应用能力

从课始的拼图导入，到课中的野餐垫大小的探究，最后到两张卡片面积的测量，这一系列生活中的问题，是通过“观察比较”抽象出数学问题，再利用如“平移”“旋转”“计算”等数学方法来解决问题的。这一过程其实就是应用意识培养的过程。尤其是课尾运用内化环节，通过选择（合适面积单位）——测量——不够怎么办？——部分密铺操作——抽象出数学模型：（长里铺几块）×（宽里铺几块）=整个图形的面积数，这也为后面的长方形面积公式的推导做好铺垫。闯关练习中运用平移、翻转等方法，把不规则图形转化为规则图形来解决问题。这些数学思想方法的运用很好地提高了学生的应用意识和创新意识。

本课通过“对比”和“体验”，以“应用实践”为推手很好地践行了陶行知的“行是知之始，知是行之成”思想，注重在实际应用中培养应用能力，实践出真知——为教学“面积和面积单位”提供了新的视角。