翼柱型量水槽应用于梯形渠道性能试验研究

刘鸿涛， 赵瑞娟，宋一梦，牛 炎， 于明舟， 韩 宇， 屈忠义

(1.长春工程学院 水利与环境工程学院，长春 130012；2.内蒙古农业大学水利与土木建筑工程学院，呼和浩特 010018； 3.吉林省水工程安全与灾害防治工程实验室，长春；130012；4.松辽水利委员会，长春 130012； 5.长春市水利勘测设计研究院，长春 130012；6.中国农业大学水利与土木工程学院，北京 100083)

灌区作为农业用水大户，其用水计量与管理尤为重要，与灌溉渠道相配套的量水设施研发具有重要意义。研究表明，堰槽类量水设施经济实用且稳定可靠，适合在灌区大规模推广应用[1-3]。随着灌区量水技术的不断发展，涌现出了一大批量水槽形式，如长喉道、短喉道和无喉道量水槽[4,5]，以及抛物线形、半圆柱形等新型量水槽[6,7]。吕宏兴于2003年提出了仿真机翼形状的机翼形量水槽[8]。但是针对不同的量水槽形式，其适用的渠道形式和收缩比范围不同，而且在部分高含沙、缓坡降的灌区，现有量水建筑物存在淹没度高、测量精度不够、水头损失大的问题。

翼柱型量水槽是剖面为对称翼形沿渠道中心线修砌，其具有结构简单，便于修建，省工省料，水头损失小，用于灌溉渠道量水精度较高的特点。其过流表面为减缓曲线，几乎无水流突变现象，水流条件好且不易产生淤积。

本文针对翼柱型量水槽在梯形渠道采用4种收缩比进行试验研究，分析其测流精度、水头损失、佛汝德数、临界淹没度等水力性能参数，为翼柱型量水槽在灌区最为常用的梯形渠道应用选型提供参考。

1 试验设计及测流原理

1.1 模型试验设计

试验系统由地下水库、供水管道、水泵、稳水池、梯形渠道及排水池组成。梯形渠道底宽0.60 m，渠深0.36 m，渠道边坡系数为1。梯形渠道翼柱型量水槽结构见图1。

图1 翼柱型量水槽平剖面图

翼柱型量水槽基本参数见表1。

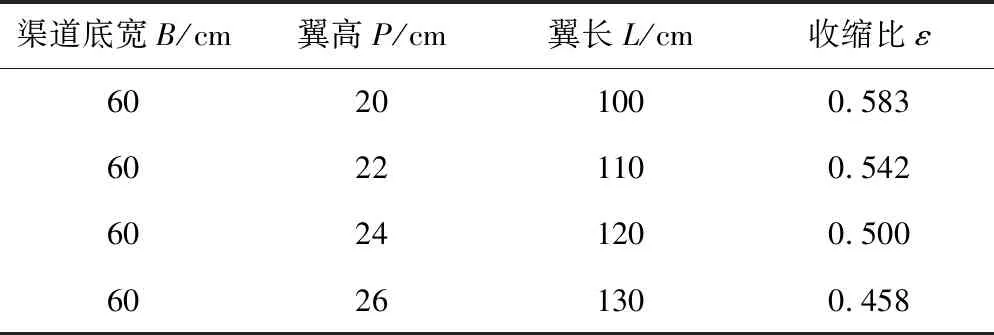
表1 量水槽基本参数

收缩比计算公式如下：

(1)

式中：ε为收缩比；Mc为喉口断面面积，m2；M为渠道断面面积，m2。

梯形渠道翼柱型量水槽试验分别在0.583、0.542、0.500、0.458四种不同收缩比情况下进行，试验流量由水泵变频机组供给，调节幅度为10～80 L/s。

试验中需要测量数据有渠道流量、量水槽上下游水深、量水槽喉口断面水深等。流量数据由DN200～B2C1D3法兰连接型管道电磁流量计(测量精度为0.1 %)量测，水深数据采用SCM60型数显水位测针(测量精度为±0.18 mm)读取。

1.2 测流原理

翼柱型量水槽是一种根据文丘里原理设计的量水槽，水流流经渠道两侧的束窄断面，发生能量交换，使上游水深与流量之间形成稳定的线性相关关系。量水槽实物见图2。

图2 翼柱型量水槽模型试验照片

2 结果与分析

2.1 流量公式与测流精度

文丘里槽过槽流量理论上一般与上游稳定水位H3/2成正比，不同收缩比情况下，翼柱型量水槽H3/2与流量关系见图3，由图3可知，不同收缩比条件下，试验流量Q与量水槽上游水位H3/2几乎位于一条直线上，具有很好的线性相关性。R2均大于0.997 1。

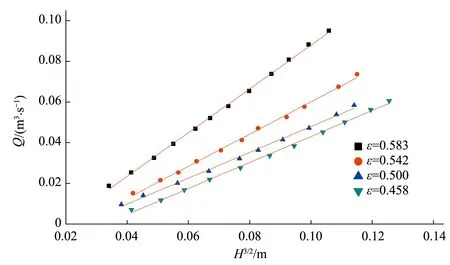
图3 模型试验流量Q与H3/2关系图

通过拟合得到4种不同收缩比的梯形渠道翼柱型量水槽流量计算公式，见表2。

图4为试验实测流量与公式计算流量的对比图，由图4可知，二者相关关系极好，R2高达0.998 6。

梯形渠道翼柱型量水槽测流相对误差计算公式如下：

表2 梯形渠道翼柱型量水槽流量公式

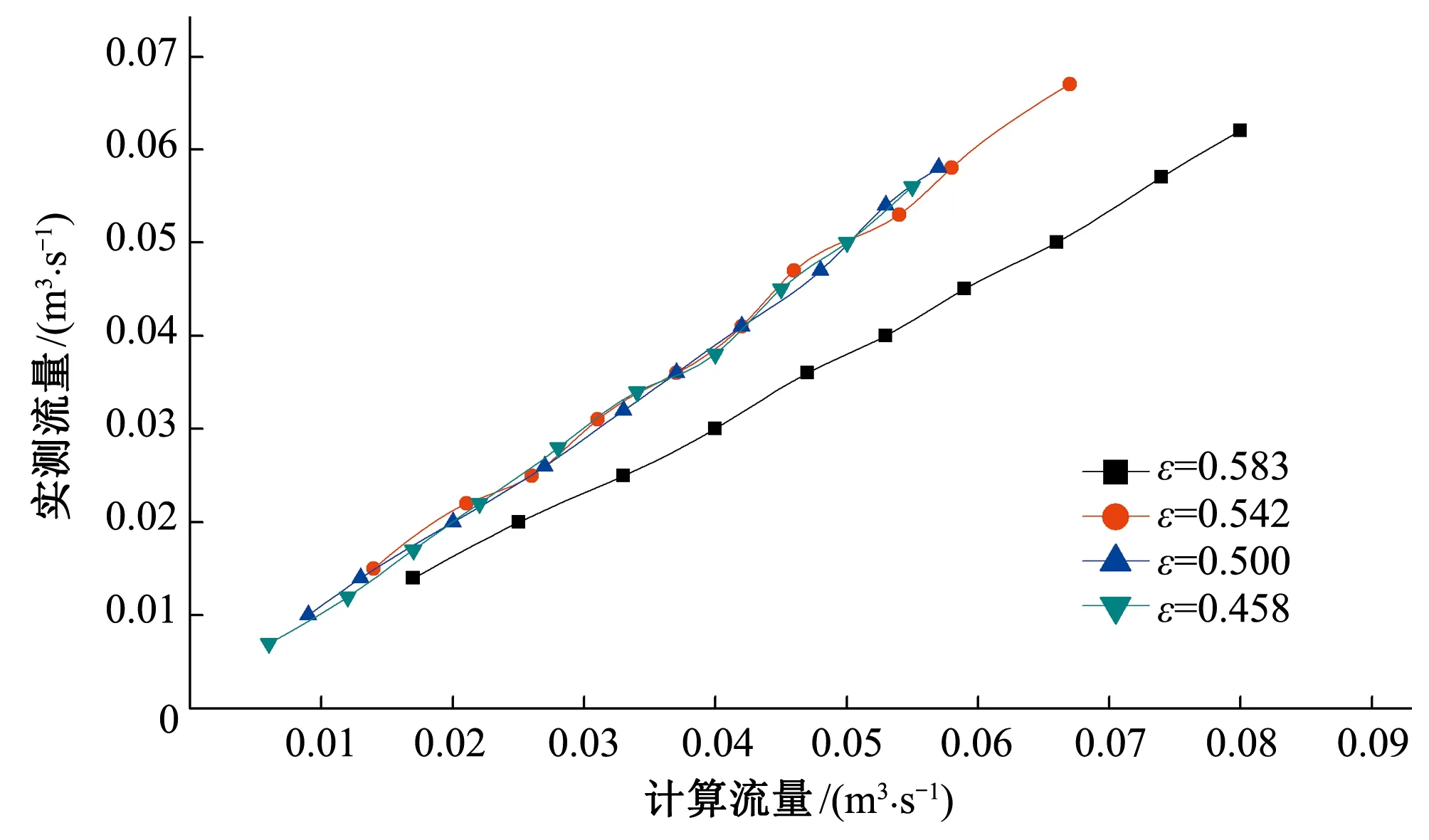
图4 实测流量与计算流量比较

(2)

式中：e为测流相对误差；Qc为表2公式计算流量，m3/s；Qm为试验实测流量，m3/s。

通过上式计算得到梯形渠道翼柱型量水槽测流相对误差范围为0.41%～3.55%，平均相对误差可达2.41%，满足我国《灌溉渠道系统量水规范》(GB/T 21303-2017)[11]要求。

2.2 临界淹没度

梯形渠道翼柱型量水槽临界淹没度最大可达0.899。说明在梯形渠道，翼柱型量水槽具有较大的自由出流范围。图5为不同收缩比翼柱型量水槽临界淹没度与过槽流量之间的关系。

图5 流量Q与临界淹没度关系

2.3 量水槽上游佛汝德数

佛汝德数Fr作为明渠水流流态的判别标准，是衡量量水槽量水性能优劣的重要指标，其计算公式如下：

(3)

式中：v为渠道断面平均流速，m/s；g为重力加速度，m/s2；h为断面平均水深，m。

通过对试验数据进行整理计算，得到不同收缩比条件下流量与佛汝德数的关系，如图6所示。由图6可知，4种不同收缩比情况下，翼柱型量水槽佛汝德数均小于0.4，满足《灌溉渠道系统量水规范》(GB/T 21303-2017)中Fr<0.5的量水要求[11]。同理可发现，梯形渠道翼柱型量水槽上游佛汝德数与收缩比有关，与二者均成正比关系。

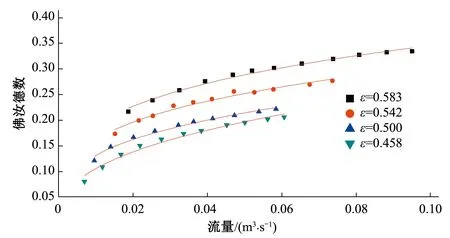
图6 不同收缩比ε条件下流量Q与佛汝德数Fr关系

2.4 壅水高度

由于量水槽修筑于渠道中间，势必会产生壅水，壅水过高不但会影响测流精度，也会造成水源浪费。壅水高度为量水槽上游稳定水位与下游稳定水位之间的差值。对试验数据进行初步分析，发现渠道壅水高度呈现与量水槽收缩比成反比，与过槽流量成正比的关系。经过计算可知，梯形渠道翼柱型量水槽最大壅水高度占渠道正常水深的29.7 %，平均壅水高度占渠道正常水深的20.6 %。渠道设计超高的计算公式如下：

H0=0.25h0+ha

(4)

式中：H0为渠道设计超高，m；h0为渠道壅水后的加大水深，m；ha为渠道安全量，可取0.2 m。

梯形渠道翼柱型量水槽上游壅水高度均小于渠道设计超高，可以满足灌区既成渠道的应用要求。

2.5 水头损失

根据能量方程，可推知量水槽水头损失公式如下：

(5)

式中：hj为水头损失，m；h1量水槽上游断面水深，m；h2为量水槽下游某断面水深，m；v1为量水槽上游某断面流速，m/s；v2为量水槽下游某断面流速，m/s；α为动能修正系数，取1；g为重力加速度，m/s2。

表3为不同流量条件下，梯形渠道翼柱型量水槽水头损失与上游总水头的对比情况，以百分数形式呈现。由表3可知，水流流经梯形渠道翼柱型量水槽产生的水头损失范围为7.12%～29.51%，同一流量条件下，水头损失随量水槽收缩比的增大而减小，同一收缩比条件下，水头损失随渠道流量的增大而增大。

3 结 语

(1)梯形渠道翼柱型量水槽流量公式测流平均误差为2.41%，满足《灌溉渠道系统量水规范》(GB/T 21303-2017)[11]的要求。

(2)梯形渠道翼柱型量水槽上游佛汝德数Fr均小于0.4，满足规范要求，上游佛汝德数随收缩比和流量的增大而增大。

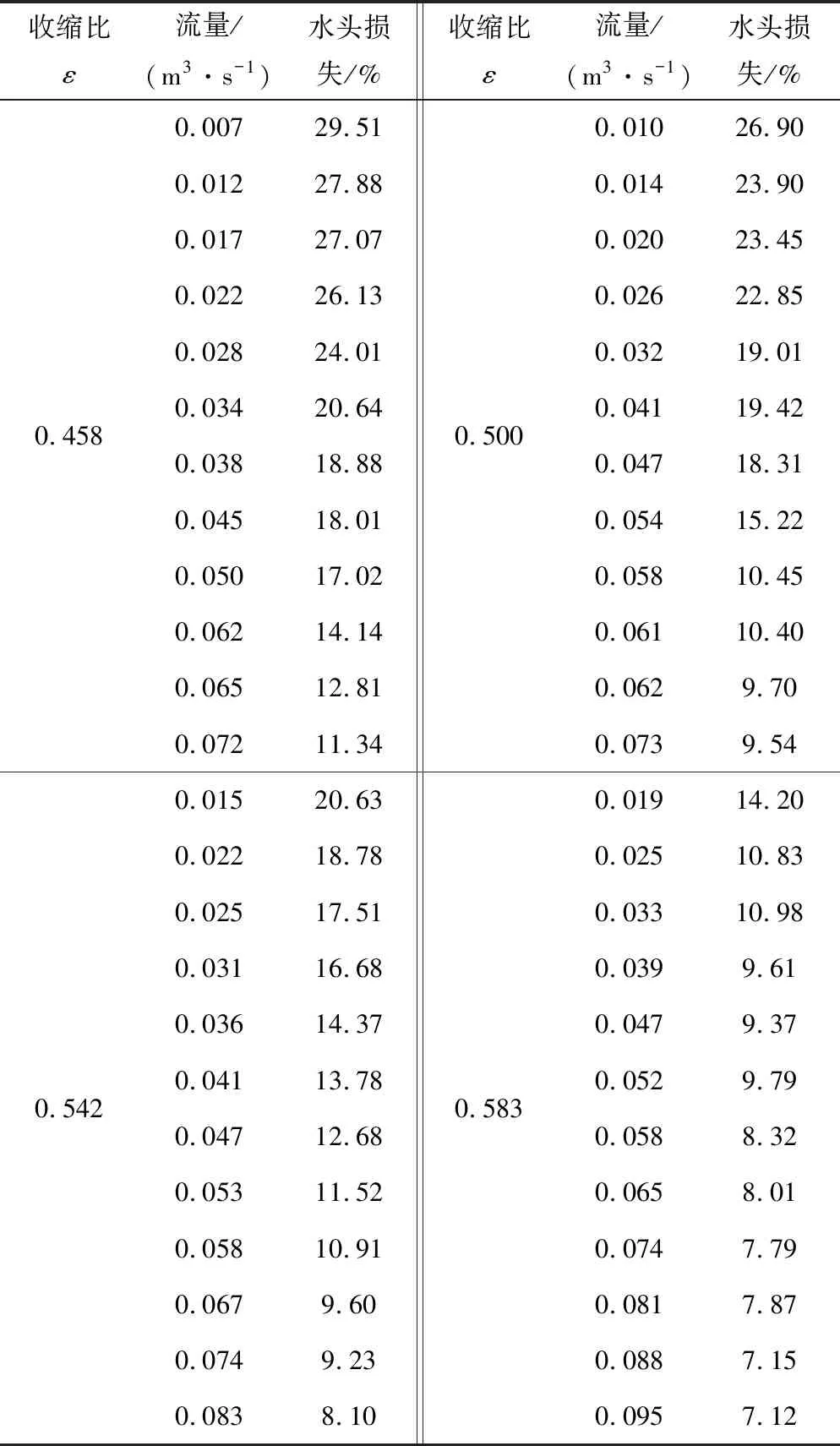
表3 不同流量水头损失计算表

(3)梯形渠道翼柱型量水槽临界淹没度高达0.899，在梯形渠道具有较大的应用范围。

(4)水流经过量水槽产生的水头损失范围为7.12%～29.51%，且收缩比越大，水头损失越小。

(5)梯形渠道翼柱型量水槽测流精度较高，各项量水性能较好。适合在灌区末级渠道推广应用。