自然通风建筑内空气流动和污染物扩散的数值模拟

谢海英，沐贤维，李 晓，王晓晓，黄 山

（上海理工大学 环境与建筑学院，上海 200093）

建筑内的空气污染可采用自然通风方式去除，研究者大多采用现场测量、风洞试验及数值模拟等方法考察室内通风效果和空气污染物迁移扩散情况［1-4］。考虑到数值模拟法成本低、周期短，本文利用Fluent软件模拟单体建筑模型自然通风时室内外空气流动和污染物扩散。利用数值模拟法研究空气污染物扩散问题时，需要选择合适的紊流施密特数（Sct），但已有研究大多采用软件的默认值，而较少考虑Sct的选取问题［5-7］。因此，本文选取不同的紊流模型和Sct，并利用已有的风洞试验数据［3］验证建筑内流场和污染物浓度场模拟值，据此评判紊流模型的预测能力并给出Sct的合理取值范围。

1 计算模型

风洞试验［3］研究了单体建筑自然通风时室内气流和污染物浓度的分布。图1是根据风洞试验［3］给出的数值模拟的单体建筑模型和计算域示意图。该建筑模型与原型的比例为1∶100，模型的长（L）、宽（W）和高（H）见图 1（a），坐标系的原点位于建筑物迎风面底部的中点，并定义x向、y向和z向的速度分别为u、v和w。在模型的迎风面和背风面处均有一位置和尺寸相同的窗口，且窗口均关于y= 0平面对称，窗口尺寸及位置见图1（a）。x向上建筑物迎风面距离计算域入口边界3H；建筑物背风面距离出口边界15H；y向上建筑物与计算域侧面的距离为5H；z向上建筑物顶部距离计算域顶面5H［8-10］。

定义计算域进口面上z=H处x向速度为UH。风洞试验中流场测量和浓度场测量采用相似的来流风速廓线，但UH不同：流场测量时UH为4.3 m·s-1；浓度场测量时UH为2.2 m·s-1。根据风洞试验采用Fluent软件自定义函数UDF（user defined function）拟合出计算域进口风速廓线，结果如图2所示。模拟浓度场时，按风洞试验选取乙烷（C2H4）与空气的混合气体代替污染物。污染源为点源，且位于模型内地面中心位置，释放口尺寸为8 mm × 8 mm，C2H4的体积分数为 5×10-3［3］。

图1 建筑模型和计算域示意图(单位：m)Fig.1 Isolated building model and the computational domain

计算域进口采用图2给定的来流条件，出口采用出流条件，其余墙面为固壁边界条件。网格由商用软件ICEM生成，为非结构网格，建筑模型周围网格细化处理。经网格独立性验证，本文选取网格数量约为4.5 × 106。所模拟的建筑内外无温差，控制方程为连续性方程、Navier-Stokes方程、紊流模型方程以及组分输运方程，方程具体形式参见文献［11］。控制方程采用二阶迎风离散格式，计算收敛的标准为残差达到1.0 × 10-5，且流场和浓度场无变化。

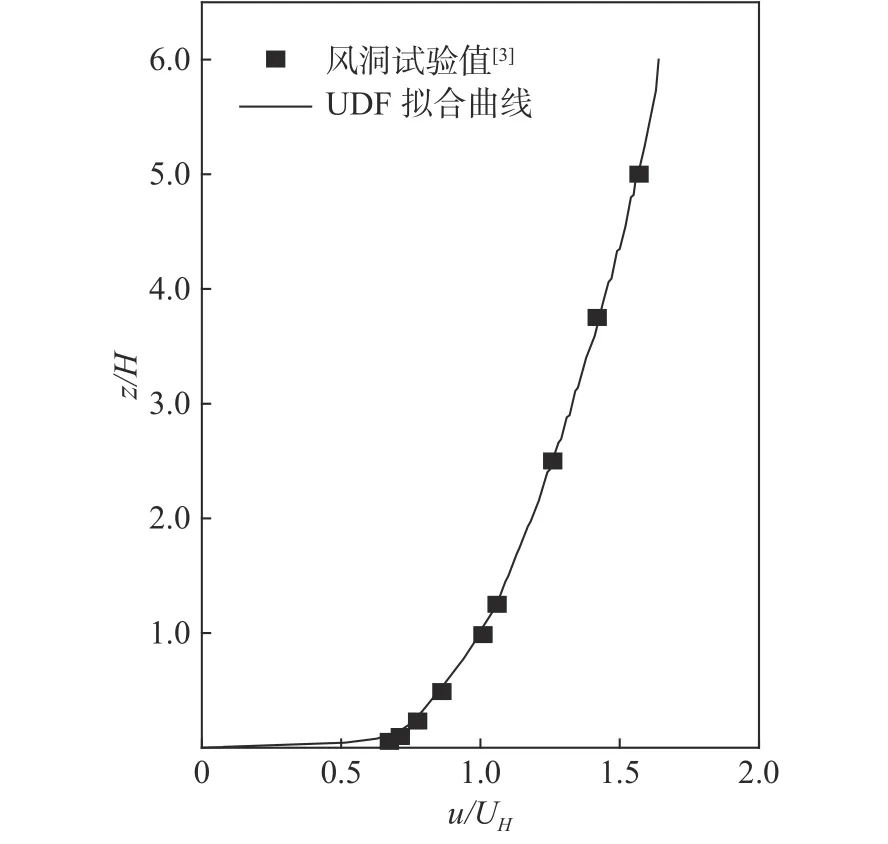
图2 来流风速廓线图Fig.2 Inlet velocity profile

2 计算结果与分析

2.1 速度场

本文首先采用标准k-ε紊流模型模拟了来流风速UH分别为4.3、2.2 m·s-1时的流场。图3为建筑内不同位置处u/UH的风洞试验值（UH= 4.3 m·s-1）和模拟值的比较，图中速度的测点是建筑物对称面（y= 0）上间距均匀的7条垂线，并依次命名为位置a、b、c、d、e、f和g[见图 3（h）]。由图 3中可知：UH= 4.3 m·s-1时速度场的模拟值在z/H＞ 0.6时和试验值吻合得较好；当0.2 ＜z/H＜ 0.6时，计算值略大于试验值；当z/H＜ 0.2时，模拟值略小于试验值。由图3中还可知，UH= 2.2 m·s-1时各位置上模拟的速度分布特征与UH= 4.3 m·s-1时的基本相似，且地面附近的模拟值与试验值吻合得更好。数值模拟结果表明，UH分别为4.3、2.2 m·s-1时，建筑内的流场基本相似。

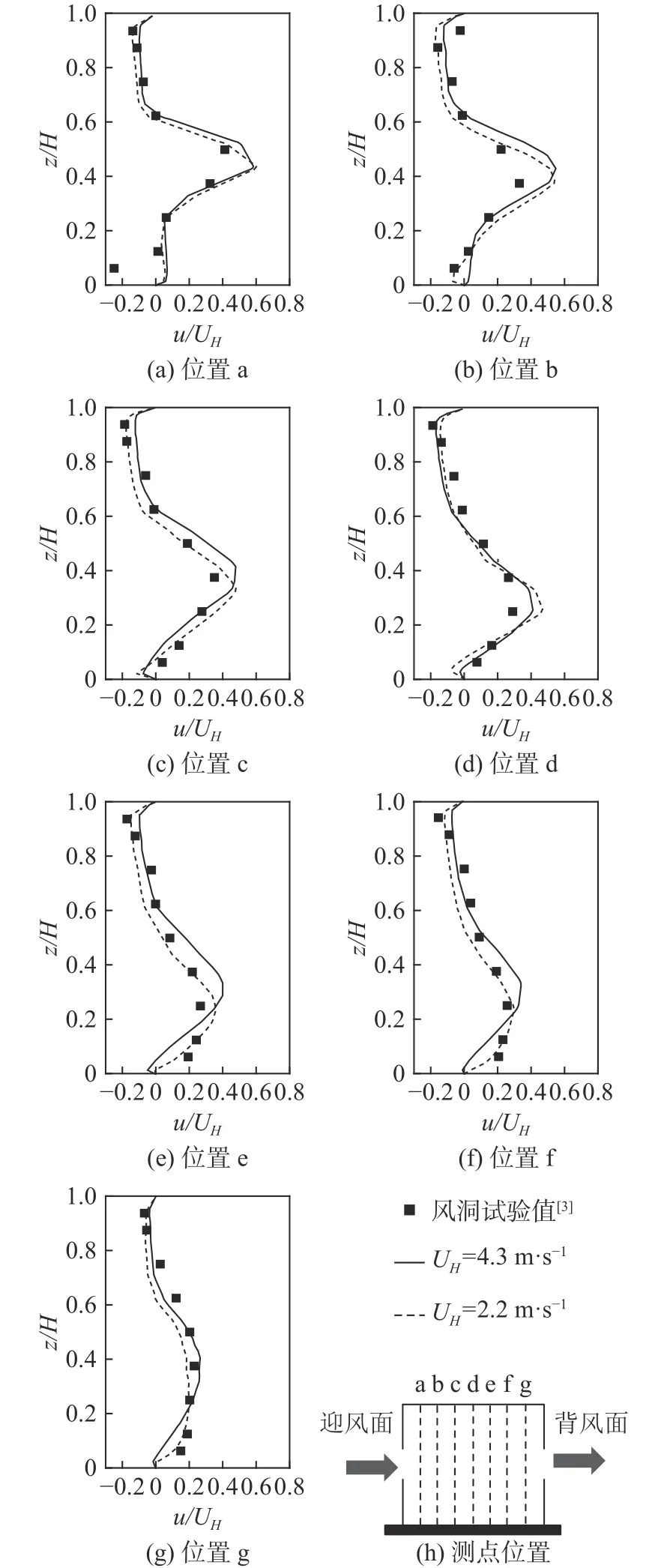
图3 标准k-ε模型模拟值和风洞试验值的比较Fig.3 Comparison between the simulation results with standard k-ε model and the measured results in the wind tunnel

图4为UH= 4.3 m·s-1时建筑内对称面（y=0）上的流线。由图中知，在靠近建筑迎风面窗口的地面附近，计算的回流区范围明显大于试验测得的范围，且涡心位置更远离迎风面的窗口。

风洞试验测量了无量纲通风量Q*，Q* =Q/（UHAin），其中：Q为通风量；Ain为窗口面积。表1为Q*模拟值和试验值的比较。由表1中可知，两种来流风速下，通风量的模拟值都略小于试验值。

为比较不同紊流模型的预测效果，本文给出了 realizablek-ε模型和 RNGk-ε模型的模拟值。图5为不同紊流模型在UH= 2.2 m·s-1时u/UH的模拟值和风洞试验值的比较。由图中可知，3种模型的模拟值及其和试验值的吻合情况基本相同，但在某些位置上有差异。

图6为建筑内各位置处k/UH2（k为紊动能）的模拟情况。由图中可知，在建筑内大部分位置，k的模拟值小于试验值，尤其在建筑物中上部区域，RNGk-ε模型的模拟值在建筑中部明显小于标准k-ε模型和realizablek-ε模型的模拟值。

图4 UH = 4.3 m·s-1时标准-模型模拟得的流线和风洞试验得到的流线比较Fig.4 Comparison of streamlines between the simulation results with standard k-ε model and the measured results in the wind tunnel at UH=4.3 m·s-1

表1 Q＊的模拟值和试验值比较Tab.1 Comparison of non-dimensional ventilation rate between the simulation and experiments

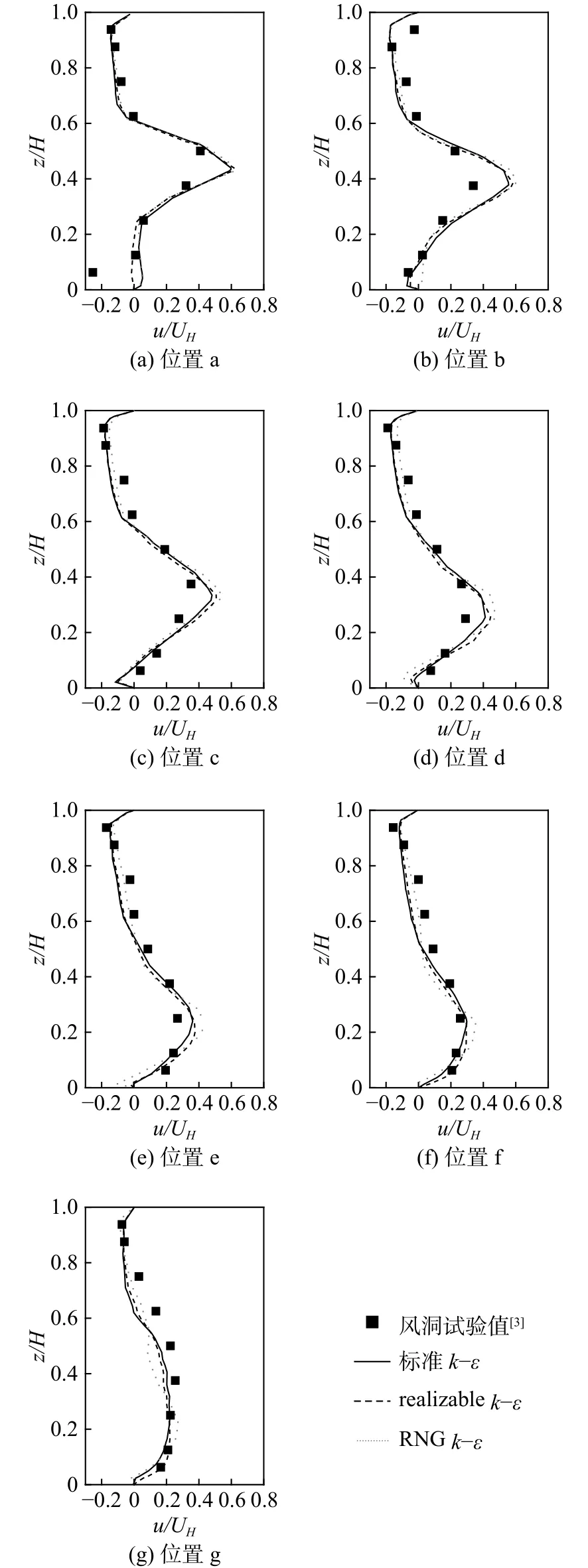
图5 3种紊流模型u/UH模拟值和风洞试验值的比较Fig.5 Comparison of u/UH between the simulation results from three turbulence models and the measured results in the wind tunnel

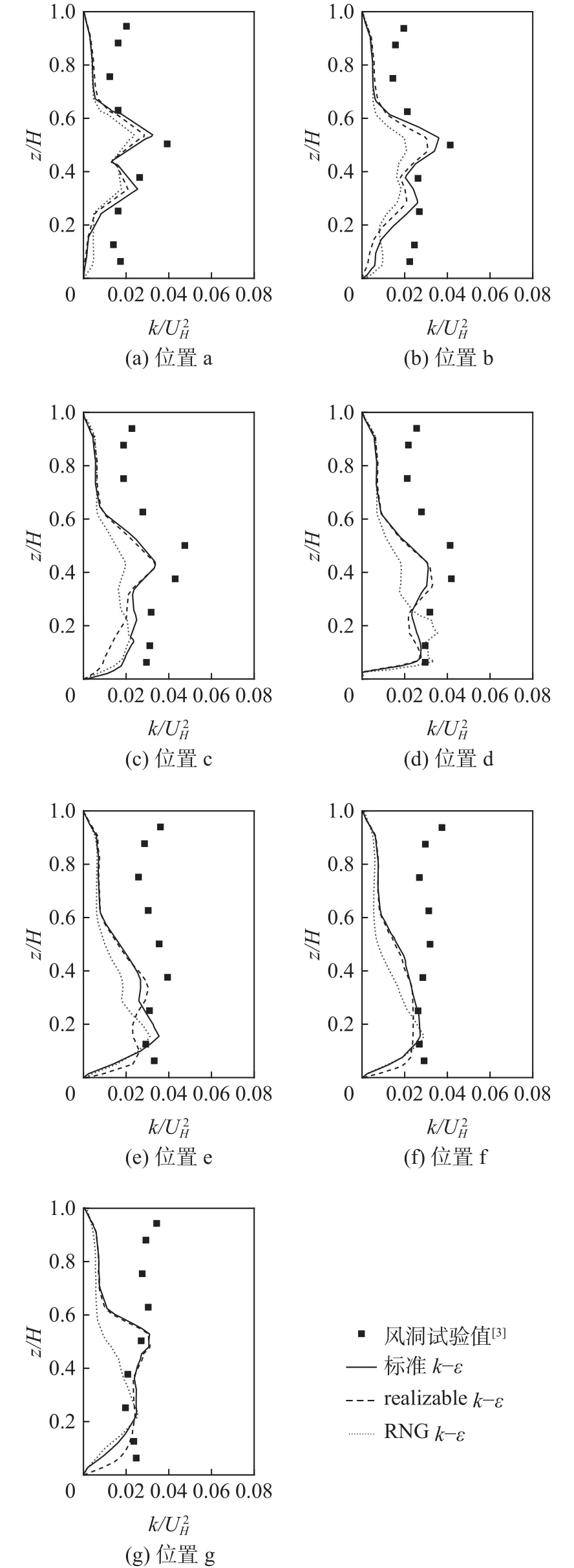
图63种紊流模型模拟值和风洞试验值比较Fig.6 Comparison ofbetween the simulation results from three turbulence models and the measured results in the wind tunnel

2.2 浓度场

依据前文模拟的流场，本文求解了组分输运方程并获得了浓度场。为考察Sct对浓度场的影响，组分输运方程中的Sct分别取 0.3、0.4、0.5、0.6、0.7、0.8、0.9、1.0。为方便比较，本文按风洞试验定义了C2H4的无量纲浓度c/C0，其中c为C2H4的体积分数，C0=qe/（H2UH），其中qe为释放率，单位为m3·s-1。

2.2.1 标准 k-ε模型

图7为标准k-ε模型在不同Sct时c/C0的分布情况。由于进、出风口位置形成了贯穿气流，因此建筑内上、下空间的空气流动被分割开来。同时，污染源位于建筑内地面中心位置，这导致污染物主要集中在地面附近，并且位置d的地面附近污染物浓度最大。然而，不同位置处的c/C0随Sct的变化情况并不相同，需结合流场模拟情况逐一分析。

位置a和b靠近地面处是进风口下方的回流区。由于标准k-ε模型模拟的回流区范围比实测的大（见图4），且位置a和b的地面处紊流强度模拟值小于试验值 [见图 6（a）、（b）]，因此，偏强的对流和偏弱的紊动能均使得这些位置的浓度模拟值大于试验值。因Sct=vt/Dt（vt为紊流动量扩散系数，Dt为紊流质量扩散系数）［12］，则当Sct＜ 1时，污染物的紊流扩散系数大于紊流动量扩散系数。当Sct取值越小（如Sct= 0.3），即人为增加污染物的紊流扩散强度，位置a和b的地面处浓度模拟值才能更接近试验值[见图7（a）、（b）]。因此，虽然Sct= 0.3时的模拟情况更好，但这是采用较小的Sct去修正流场预测不准确所带来的影响。

从图 7（c）～（g）中可知，Sct取 0.8～1.0时，浓度模拟值与试验值的吻合程度比Sct取0.3～0.7时好。与位置a和 b的地面处流场模拟值相比，标准k-ε模型能较好地给出位置c～g 地面处的时均速度 [见图 5（c）～（g）]和紊动能分布 [见图 6（c）～（g）]。结果表明，在流场模拟基本准确的情况下，模拟污染物的Sct应为0.8～1.0。

从图 7（d）～（e）中可知，在位置 d和 e的z/H=0.3附近，浓度模拟值远小于试验值，这可能是因为此处计算的u偏大所导致[见图5（d）～（e）]。当z/H＞ 0.5时，c/C0均较小，试验值和模拟值吻合较好，浓度模拟值随Sct的变化不明显。

2.2.2 realizable k-ε模型

图8为采用realizablek-ε模型在不同Sct时c/C0的分布情况。由于realizablek-ε模型与标准k-ε模型的流场模拟情况基本一致（见图5、6），因此其浓度分布也基本相同（见图7、8）。由图 6（a）～（c）中可知，realizablek-ε模型在位置a～c地面附近（z/H＜ 0.2）给出的紊动能略小于标准k-ε模型的值，因此，这些位置地面处的c/C0略大于标准k-ε模型的值。在位置 f～g的地面附近，realizablek-ε模型给出的紊动能比标准k-ε模型的略大 [见图 6（f）～（g）]，因此，这些位置的c/C0会略小于标准k-ε模型的值，但差异较小。总的说来，Sct在0.8～1.0时，realizablek-ε模型的浓度值和试验值吻合得较好。

2.2.3 RNG k-ε模型

图9为 RNGk-ε模型在不同Sct时c/C0的分布情况。由图5（d）中知，在位置d的地面附近（z/H＜ 0.1），RNGk-ε模型的u明显大于另外两种模型的值，且u与试验值方向相反。因为污染源正位于此处，所以污染物被对流传输至位置 c，因此，RNGk-ε模型在位置 a～c的c/C0都明显增大 [见图 9（a）～（c）]。在位置 e的地面附近（z/H＜ 0.1），RNGk-ε模型的u依然有反向和偏大的特点，因此，图9（e）～（g）的地面附近浓度比标准k-ε模型的小，也小于试验值。由于RNGk-ε模型对地面附近流动预测不理想，因此，Sct无论取较小值（0.3～0.4）还是较大值（0.8～1.0），浓度模拟值和试验值的吻合结果均不理想。

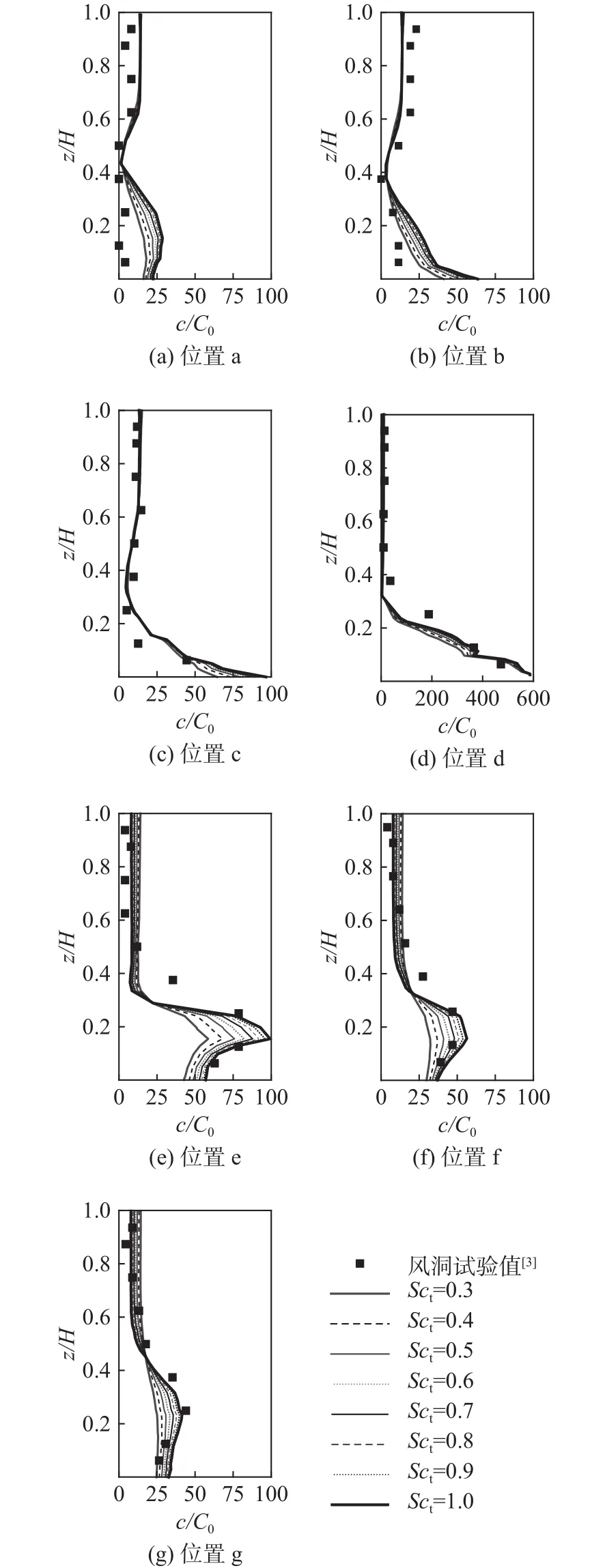
图7 标准 -， = 0.3～1.0时和风洞试验值比较Fig.7 Comparison of between the simulation results with standard - model and the measured results in the wind tunnel when =0.3～1.0

3 结 论

本文采用3种紊流模型（标准k-ε模型、realizablek-ε模型和RNGk-ε模型）数值模拟了单体建筑自然通风的流场和室内地面有点源时的气体污染物浓度场，考察了Sct对浓度场的影响，得出以下结论：

（1）3种紊流模型对单体自然通风建筑的室内速度场（包括主流方向的时均速度和紊动能）预测存在一定的差异，尤其是地面附近。测点位置的时均速度及地面附近的紊动能与试验值基本吻合，通风量的模拟值均略小于试验值。

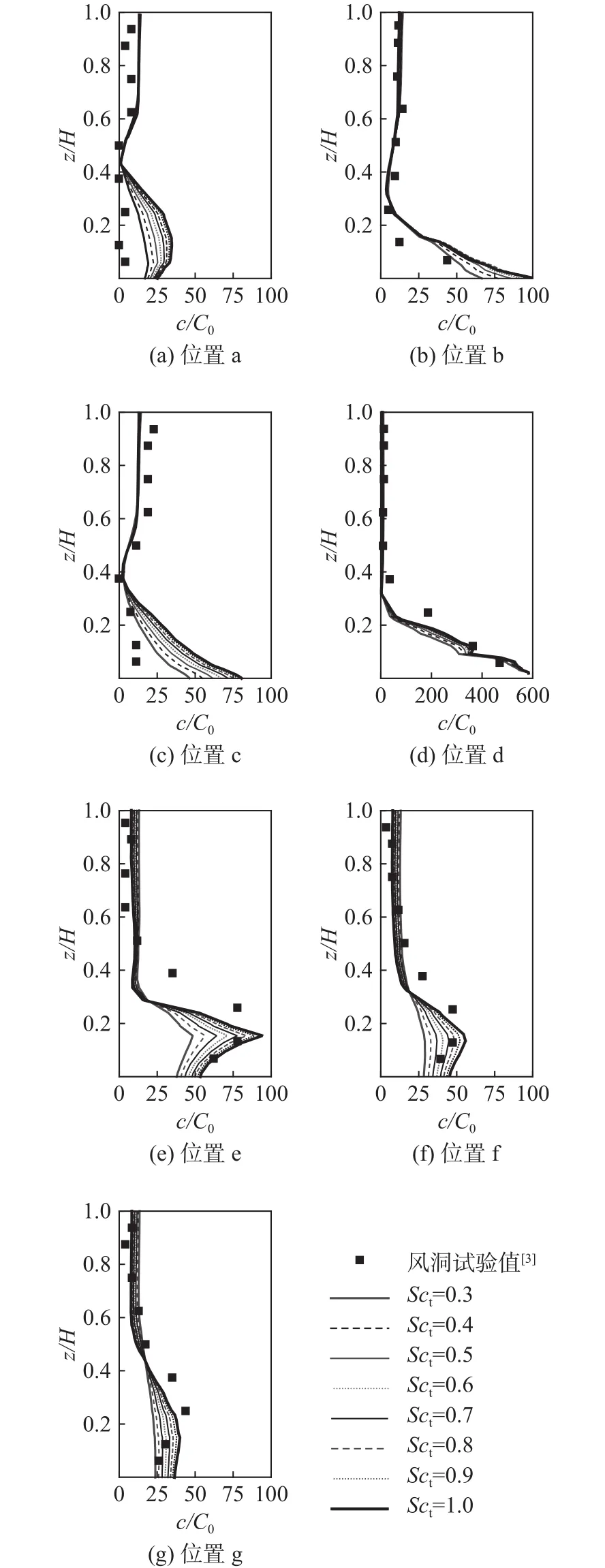
图8 realizable = 0.3～1.0时与风洞试验值比较Fig.8 Comparison ofbetween the simulation results with realizablemodel and the measured results in the wind tunnel when=0.3～1.0

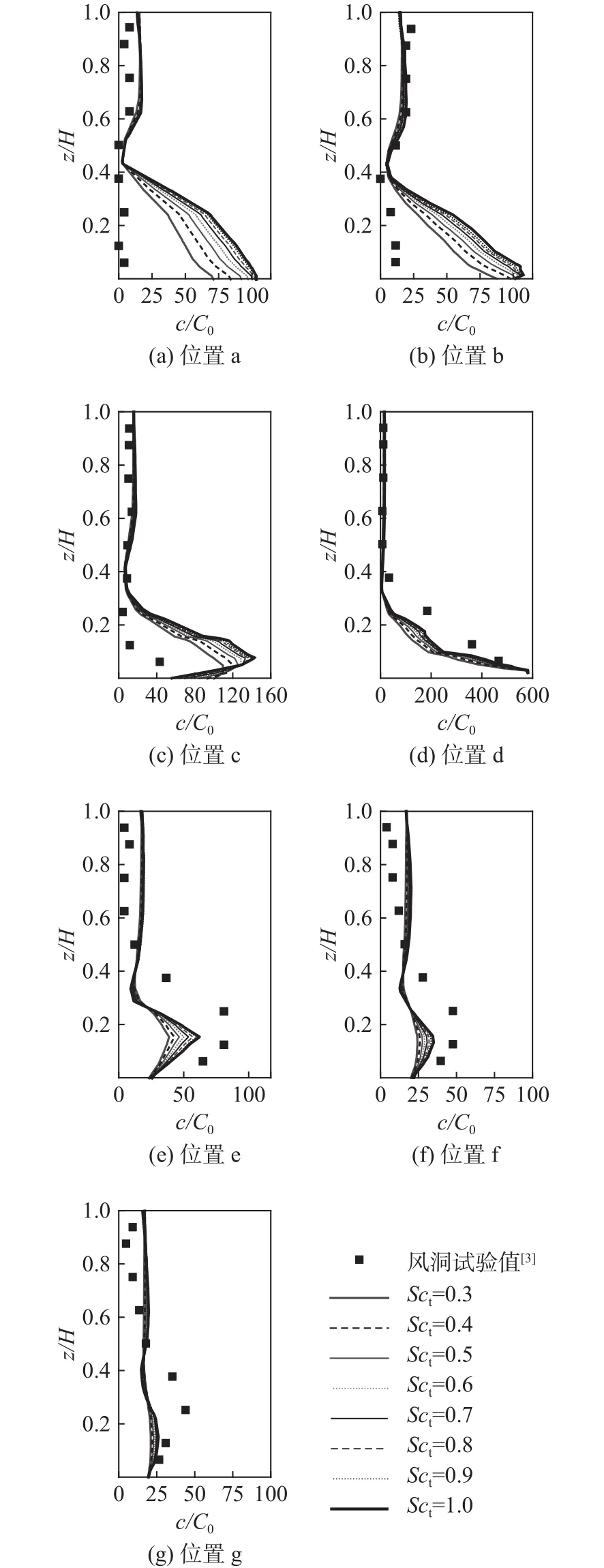
图9 RNG = 0.3～1.0时与风洞试验值比较Fig.9 Comparison ofbetween the simulation results with RNGmodel and the measured results in the wind tunnel when=0.3～1.0

（2）Sct取值会显著影响源附近高浓度区的模拟值。相比于RNGk-ε模型，标准k-ε模型与realizablek-ε模型模拟的流场更相似，大部分位置的流场模拟值与试验值吻合得较好，因此其浓度场也基本相同。当Sct为0.8～1.0时，浓度模拟值和风洞试验值吻合得最好。由于RNGk-ε模型对地面附近时均速度预测不理想，因此，无论Sct如何选取，浓度模拟值和试验值都相差较大。

（3）根据浓度模拟值和试验值的吻合程度确定最佳Sct取值时，应保证时均速度和紊流强度的预测准确。若无流场的试验验证，则选取的最佳Sct可能并不可靠。