厘清脉络 建构联系 感悟思想

徐月红　倪芳华

【教学内容】

苏教版六年级下册教科书第94页“整理与反思”，完成94—95页“练习与实践”第1—7题。

【教学目标】

1.使学生经历整理立体图形表面积、体积有关知识的过程，进一步理解立体图形的表面积、体积（容积）的含义，掌握常用的体积（容积）单位，以及相邻单位间的进率，理解和掌握常见几何体的表面积和体积计算方法，能正确进行有关立体图形的表面积和体积（容积）计算。

2.使学生在梳理相关知识的过程中，构建直柱体之间的内在联系，使知识结构化，发展学生的空间观念，培养类比、推理能力，增强合作意识。

3.使学生在整理立体图形的有关知识、运用所学知识解决问题的过程中，进一步体会立体图形与现实生活的密切联系，获得学习成功体验。

【教学重点】

自主梳理，构建立体图形表面积、体积的认知结构。

【教学难点】

归纳立体图形侧面积、表面积、体积的统一计算方法。

一、创设情境，引入新课

1.出示图：这是徐老师家客厅的一角，客厅里的一些物品听我来介绍一下。

这台长方体微波炉的容积是25立方分米，这个圆柱体垃圾桶的表面积是21平方分米……

2.从数学的角度，你想到了哪些立体图形？（贴出）和这些立体图形的哪些知识？

今天这节课徐老师将协助同学们对立体图形表面积和体积的有关知识进行整理和复习。（出示课题）

二、自主整理，构建网络

1.整理立体图形的表面积和体积的意义

（1）你能结合这些例子，说说什么是立体图形的表面积、体积、和容积吗？体积和容积有怎样的联系和区别？

2.表面积、体积和容积的计量单位分别是什么？相邻单位间的进率各是多少？课前已经请同学们在学案上进行了整理，把你的整理在小组里交流，要求一人主讲，其他人补充。

【评析：新课伊始，徐老师巧妙地创设了自家客厅的生活情境，漂亮的客厅内有大家熟悉的微波炉、电冰箱、金鱼缸、垃圾桶等生活用品，教师相机提出两个问题“从数学的角度，你想到了哪些立体图形？”“你能结合这些例子，说说什么是立体图形的表面积、体积、容积吗？”让学生感受到生活中蕴藏着许多数学知识，有效激发了学生学习的兴趣，同时，也帮助学生加深对长方体、正方体、圆柱表面积和体积含义的理解。】

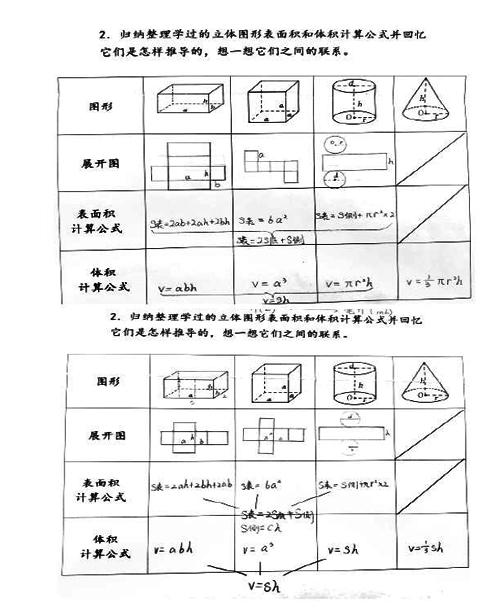
2.整理表面积计算方法

（1）师：结合具体的物体我们一起回顾了立体图形表面积、体积、容积的意义，以及计量单位，课前同学们对他们各自的计算方法也作了整理，拿出学案在小组里交流。

（2）请生上来分享自己的整理。

（3）利用一张A4纸，你能创造出哪些立体图形？这张纸与立体图形之间有什么联系？

（4）你能结合展开图和大家解释一下这些表面积公式的含义吗？教师课件动画演示。

3.整理体积计算方法

（1）表面积公式可以结合展开图来解释，那这些体积公式是怎样推导的呢？（選一个说一说）

（2）呈现体积推导关系图

（3）这些体积公式之间又有怎样的内在联系呢？想一想，在学案上填一填。

（4）为什么前面三个立体图形体积都可以用sh表示，圆锥不行呢？

教师指出：必须是上下一样粗的直柱体。

（5）我们可以这样来理解一下：演示动画图

很多个这样的正方形底面叠加成一个正方体。

很多个这样的圆形底面叠加成一个圆柱

很多个这样的长方形底面叠加成一个长方体

小结：像这样的直柱体体积都可以用底面积乘高来计算。

（6）体积间既然有联系，表面积之间是否也有联系呢？

展开图放在一起比一比，有什么相同点？

引导学生发现：S侧=Ch

S=2S底+S侧

小结：这些立体图形体积之间有内在联系，表面积之间也有内在联系，这就是我们数学的逻辑之美。结合大家的智慧我们完成了这个整理，这里有旧知识也有发现的新知识，请每个同学再次完善自己的整理。

【评析：教师精心设计学习单，放手让学生课前进行归纳、整理、探究，有效唤醒他们对分散所学到的关于立体图形的表面积和体积的各部分认知，以便于学生清晰地认识这些立体图形的特征，有助于他们加深对展开图与立体图形对应关系的认识。教师将表面积的意义与计算方法结合起来复习，将立体图形公式推导联系起来思考，将三维立体图形和二维平面图形相互转化，巧妙地进行系统整理，让学生从面到体构建起联系，获得清晰的直观表象，深悟转化思想，发展空间观念和推理能力。】

三、联系生活，应用拓展。

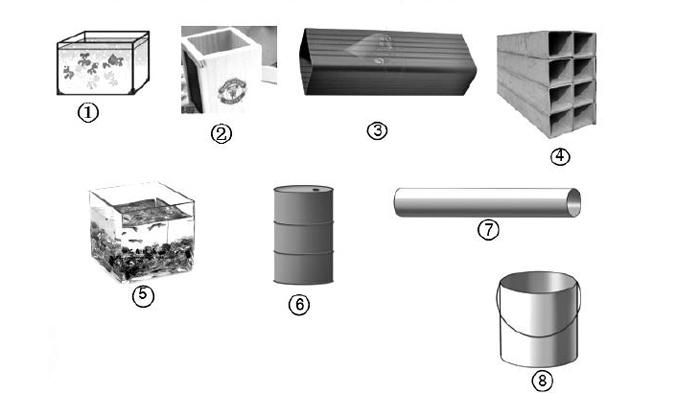
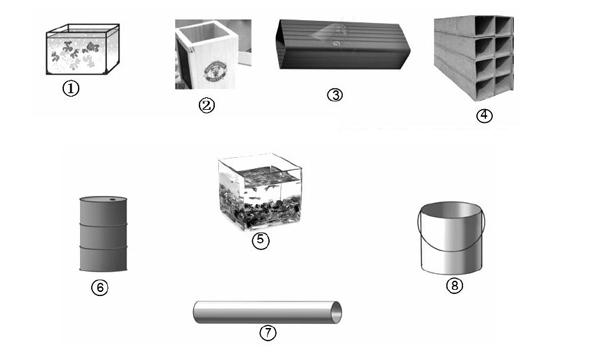
1.看看黑板上这些立体图形在我们生活中的样子（出示）

（1）灵活计算这些物体的表面积

①结合这些立体图形分类，第一类都是长方体，它们的表面积在计算的时候有什么不同？结合这个长方体来说一说。（用字母表示）

②这些长方体中有没有特殊的长方体呢？出示贴出。

③结合这个特殊的长方体说说这个笔筒还可以怎么算？

④你能用这样的方法，结合这些立体图形，看看下面这几个物体的表面积怎么算？用字母在图形旁表示一下。

⑤6号图形表面积可以用底面周长乘高，这里还有哪些物体表面积也可以这样算？（3号和4号）

（2）这些物体的体积可以怎样算？（直柱体都可以用底面积乘高来计算）

小结：我们发现这许许多多的物体的表面积和体积的计算，最后都回到了这几个简单的立体图形，可不要小看这几个基本的立体图形哦，它可是帮助我们建立空间观念的好帮手。

2.先想一想立体图形的样子，再算一算

给长方体罐头盒的四周贴上漂亮的彩纸。罐头盒长12cm，宽8cm，高10cm，至少需要多少cm2的彩纸？（还可以怎样算？）

3.想一想、比一比、算一算

如果以AB边为轴旋转一周，得到的立体图形的体积是多少立方厘米？

如果以CD边为轴旋转一周，得到的立体图形的体积是多少立方厘米？

【评析：徐老师精心设计了在生活情境中解决问题的练习题，充分发挥了复习的查漏补缺和巩固提升功能，同时也打通理和练的“通道”。第一组题，尽管都是求生活中長方体实物的表面积，但所求的面不尽相同，需要认真观察、仔细辨析，要结合具体问题来解决，促进学生对所学知识理解和明晰。第二组题求物体的体积，让学生自觉运用所学知识解决实际问题，学会“数学”地思维。第三题适时进行了延伸、拓宽，促进学生知识体系的完善和思维能力的提升。】

四、全课小结，升华提高

今天徐老师和同学们一起对立体图形的表面积和体积有关知识进行了整理和复习，我们从生活中的物体想到了黑板上的四个基本立体图形，最后又利用这几个立体图形回到了生活中去帮助我们解决一些实际问题，这就是数学，它来源于生活又回到了生活中去，希望同学们在以后的学习中也能把学到的数学知识用于生活，服务于我们的生活。

【总评】

有效的复习，要做到“温故知新，适度提升” 。复习时，如何通过对已有知识的纵向、横向梳理，连点成线，由线到面，行成知识网络，从而帮助学生形成和完善认知结构呢？

一、以基本概念为联结点，让学习充满活力

本节课的基本概念就是表面积、体积。基本概念理解得越深刻，就越具有生命力。课始，教师创设了非常熟悉而又亲切的数学情境，增强了复习课的趣味性，让复习且生且长。如徐老师提出“看到客厅实物图片，从数学的角度，你想到了哪些立体图形？和这些立体图形的哪些知识？”教师开门见山引入课题，明确本节课的学习内容，也促使学生主动把零散的知识点串联成知识线，逐步形成知识网。

二、发挥学生的主体作用，让梳理真正发生

学生是查漏补缺的主体。要让学生主动对知识点进行梳理，形成由“点”到“面”的系统知识。因此，徐老师十分重视为学生提供自主梳理的时间和空间，使学生体会数学知识、方法之间的密切联系。课前发放预学单，让学生自主整理两方面内容：一、表面积、体积和容积的计量单位分别是什么？相邻单位间的进率各是多少？你能在下面整理一下吗？二、归纳整理学过的立体图形表面积和体积计算公式并回忆它们是怎样推导的，想一想它们之间的联系（要求画出展开图、写出表面积计算公式和体积计算公式）。学生人人参与，成为复习的主人。课上，学生展示交流，呈现出来的图示法、图表法等直观简约，增强了知识点之间的联系、突出对比性。大家分享着不一样的整理方法，促进了思维提升。教师根据不同状况及时调整教学的着力点，使得复习更具有针对性。

三、以构建联系为目标，让认知结构生长

为打通学科内部的“脉络”，帮助学生构建侧面积和表面积的联系、立体图形之间的联系，教师先组织学生用一张长方形纸折一折、卷一卷，再用课件演示以长方形纸的一条边为轴将长方形旋转一周，动态感知圆柱的形成，让学生清晰地认识到长方形纸的面积与柱体侧面积的联系，从中找到蕴藏的规律，使得柱体侧面积和表面积的公式得到统一。教师再动画演示将一张正方形、长方形及圆形的纸向上叠加，分别变成正方体、长方体和圆柱体，再引导学生结合公式的推导，从“变”中寻找“不变”，沟通了“面”与“体”的关系，使学生明晰知识脉络，形成知识系统，认知结构逐步条理化、结构化。