基于层次聚类的定制产品模块划分方法研究*

吕 健，王 震，潘伟杰，赵慧亮,2，刘征宏,3

(1.贵州大学 现代制造技术教育部重点实验室，贵阳 550025；2.贵州民族大学 美术学院，贵阳 550025；3.贵阳学院 机械工程学院，贵阳 550005)

0 引言

为了在竞争激烈的市场环境中及时给用户提供满意的定制化产品，现代企业急切要求产品在设计和生产过程中具备一系列标准子配件以提高制造和装配效率及资源利用率，达到节约成本、缩短生产周期的目的[1]。作为标准化的新形式，模块化设计被认为是解决快速响应用户定制需求的有效方法[2]。模块划分方法作为模块化设计研究过程中的主要内容，其划分的结果直接影响定制化产品设计、制造、装配和维护的复杂性。

围绕定制化产品模块划分方法，众多专家学者在该领域相继进行了研究。Gu等[3]考虑了产品的功能性、可制造性、可使用性、可重用性和可回收性等多个工程目标，从问题设计、交互分析和模块形成三个主要阶段对产品进行模块分析和划分。王日君等[4]提出应用公理设计的功能域—物理域的“之字形”映射架构对产品进行逐层分解，若得到对角矩阵，分解后的子结构可单独作为一个模块，划分完成；若得到满矩阵或三角矩阵，则对子结构进行功能和结构相关性分析，运用模糊树图聚类法完成聚类。陈继文等[5]从客户需求特性、流特性和技术特性出发，基于零件功能和结构相关性构建模糊等价矩阵，动态划分功能模块，以模块内平均聚合度和模块间平均分离度对多个划分方案进行评价与决策。侯昆峰等[6]提出基于相似性和独立性分析的绿色模块化重设计方法，采用模糊综合评价法对最终设计方案进行对比评价。

模块划分属于多目标综合优化问题，难以建立统一的优化模型[7]，现有的模块划分方法比较复杂，通用性较差，而且随着产品零件数量的增加，计算量会随之增加，对模块划分方案的评价也比较局限，为此，通过分析用户需求和零件功能、结构相关性构建模糊关系矩阵，利用凝聚层次聚类方法进行聚类，然后基于信息熵理论，以产品生命周期各阶段复杂度为优化目标建立数学评价模型，对不同划分结果进行综合评价，得到最优方案。

1 模块划分方案的形成

1.1 零件关系矩阵建立

定制化产品首要目标是考虑用户个性化需求。在模块划分之前，要先对用户的个性化需求进行调研与分析，采用质量功能展开方法将不确定用户需求转化成一系列明确的产品质量特性，再转变成产品模块划分待配置零件实体。

模块化设计目的是将具有最大功能和结构相关性的零件聚合成一个模块，使模块内的聚合度和模块间的分离度达到最大，要求模块与模块之间功能和结构独立，有利于提高产品多样性、维修性和绿色性[8]，满足用户个性化定制和产品更替。为了使零件聚合成独立模块，需要综合考量零件之间功能和结构的相关性，合理定义零件之间的交互值。

首先对零件的功能特性和结构特性进行分解。功能特性是指零件所要执行的服务于产品系统性能的一系列能量传输和操作行为，主要表现为零件之间的能量流、信息流、作用力流和物质流的转换和传输。结构特性包含零件的尺寸、接口等几何特性及其排列顺序、装配形式等特征，主要包括排列、联接、装配等。如图1所示。

图1 零件特性分解示意图

其次描述零件之间相关关系，给出如表1所示的零件间相关关系定义。

表1 零件之间相关性定义

综合考虑零件i,j(i,j=1,2,…,N,N为零件总数量)之间功能和结构相关性，定量描述零件i,j之间交互值，具体描述模型如下：

(1)

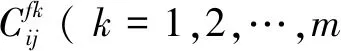
(2)

由零件i,j经过加权平均后所得综合相关度Cij建立零件关系矩阵：

(3)

其中，0≤Cij≤1，Cij=Cji，Cii=1(i,j=1,2,…,N)，关系矩阵T为对称矩阵。

1.2 基于凝聚层次聚类的模块划分

凝聚层次聚类(Agglomerative Hierarchical Clustering, AHC)是一种自下向上聚合数据的聚类算法，通过计算每一个类别的数据点与所有数据点之间的距离来确定它们之间的相似度，距离越小，相似度越高，将最为相似的两个数据点进行组合，成为一个新的数据点，替换原有的两个数据点，再进行下次聚合，并重复这一过程，最终创建一棵有层次的嵌套聚类树。

得到零件相关关系矩阵T后，由于其是相似矩阵，不一定有传递性，需要对其进行传递闭包处理，得到零件等价矩阵T′，对等价矩阵T′进行层次聚类，得到聚类树图，对其进行截割，得到不同模块划分方案。

2 面向产品生命周期的模块划分方案评价方法

产品生命周期包括产品的设计、装配、维护、更新升级、循环利用等过程，而模块划分的不同结果会直接影响产品生命周期的不同阶段，因此，在模块划分过程中应综合考虑产品生命周期过程，减少对产品的影响。

在信息论中，熵表示随机变量不确定性的度量，在系统中，熵可以用来表达系统的复杂度[9]。熵值越大，复杂度越高，系统越不稳定。每种模块划分方案构成了一个关于产品生命周期各阶段存在熵(复杂度)的系统。模块划分方案是否合理，能否实现直接取决于熵的大小。因此，把上述产品生命周期5个阶段作为优化目标，通过计算不同模块划分方案的熵值来选择最合理的划分方案[10]。

2.1 设计复杂度

模块集成的功能特性越多，其内部结构越复杂，模块的设计难度越大，同时设计中所包含的辅助功能模块也增加了设计难度。否则，模块功能少，结构简单，设计也简单。设计复杂度定义为：

(4)

式中，g为模块粒度；Mg为模块粒度g对应的模块数量；N为产品零件数量；di为第i个零件的相对变化率。

2.2 装配复杂度

模块粒度划分越细，模块数量越多，装配难度加大，装配时间变长，装配精度越难达到要求，因此，合理划分模块数量显得尤为重要。装配复杂度定义为：

(5)

式中，nt(g)为模块划分粒度为g时第t(t=1,2,…,Mg)个模块的零件数量。

2.3 维护复杂度

从设备维护角度考虑，应尽可能将易受损的零件分离开，将产品分割成多个部分以便提高维护效率，从产品的完整性来看，降低了模块维护的复杂度。维护复杂度定义为：

(6)

式中，mi为第i个零件的相对易损率。

2.4 更新升级复杂度

竞争激烈的市场环境和飞速发展的科学技术使得产品的开发周期变短、更新换代变快，产品中某些部件尚未结束功能寿命时，就被更新升级的部件所取代，因升级部分零件而放弃整个产品，明显浪费大量资源。将频繁升级的部件划分成独立模块，产品升级时只需更换升级部件，可缩短产品升级时间，提高资源利用率。更新升级复杂度定义为：

(7)

式中，ri为第i个零件的相对功能寿命。

2.5 循环利用复杂度

当整个产品废弃时，应考虑某些零件的完整性、回收性、可重用性，把产品中可回收利用的零件拆卸下来，重新应用到其他产品中，避免大量可回收资源的浪费、对环境的破坏。循环利用复杂度定义为：

(8)

式中，ci为第i个零件的相对回收率。

式(4)、式(6)、式(7)、式(8)中，di，mi，ri，ci利用层次分析法得到。

2.6 建立数学评价模型

不同阈值λ对用不同模块粒度g，对应不同模块划分方案，每种划分方案都可得到一个综合复杂度H(g)，当H(g)值最小时，系统的复杂度最低，即最佳的模块划分方案，这是一个无约束离散优化模型：

min{H(g)=Hd(g)+Ha(g)+Hm(g)+Hr(g)+Hc(g)}

(9)

2.7 模块划分结果调整

零件功能和结构特性因子权重和产品生命周期各阶段零件间相对影响率等由层次分析法得到，依靠的是专家和设计师的实际经验，存在一定主观性，在一定程度上对模块划分结果存在偏差，因此，结合实际生产情况，对划分结果进行分析，对相关矩阵做适当调整，或直接对划分结果做相应调整，得到最合理的模块划分方案。

1.显示屏 2. 出烟口 3. 传感器 4. 拨烟块1 5. 拨烟块2 6. 链条 7. 齿轮1 8. 齿轮2 9.皮带轮1 10. 皮带 11. 皮带轮2 12. 电机 13. 开关键 14. 暂停键 15. 复位键图2 立式分拣机结构简图

3 实例

现以条烟立式分拣机为例，验证上述模块划分方法的合理性和有效性。考虑到一台立式分拣机包含多条分拣烟道的特殊形制，每一条烟道可划分成一个独立的系统，其他的支撑结构及公共挡板单独作为一个模块，因此只取一条烟道为研究对象，在实际生产中根据用户需求配置相应烟道。如图2所示，立式分拣机共包括15个零件。

对条烟立式分拣机进行功能和结构特性层次划分，确定其影响模块划分的特性因子，如图3所示。

图3 立式分拣机零件特性分解示意图

由层次分析法得到图3中功能和结构各因子权重为：wf1=wf2=wf3=wf4=0.1，ws1=0.2496，ws2=0.1765，ws3=0.1019，ws4=0.072。

由式(1)可得任意零件i,j之间的综合交互值Cij，例如，零件4和6之间的综合交互值为：C(4,6)=0.1×0.8+0.1×0+0.1×0.8+0.1×0+0.2496×0+0.1765×0+0.1019×0.9+0.072×0=0.252。

由此可得零件之间关系矩阵T，应用传递闭包循环计算T的模糊等价矩阵T′，如表2所示。

表2 模糊等价矩阵T′

续表

由表2可知，对角线上的数值为1，表示零件与自身相比，相关性最大。运用凝聚层次聚类法对等价矩阵T′进行截取，如图4所示。不同λ截割会得到不同的模块划分方案，当λ取0或1时，相应的模块数为1或15，没有划分意义。

图4 立式分拣机零件聚类树图

表3是产品零件的相对变化率di，相对易损率mi，相对功能寿命ri，相对回收率ci。表4是模块划分粒度为g时第t个模块的零件个数。

表3 零件生命周期各阶段相对率

表4 模块粒度g对应模块零件数量

利用式(4)～式(8)计算可得不同λ取值时不同的模块划分方案，如表5所示。由表可得，当λ=0.226时，对应的总复杂度最小，表明该划分方案为最优方案，最终划分方案如图5所示。

表5 模块划分方案

图5 立式分拣机模块划分方案

如图5可知，零件4,5,6,7,8,9,10,11,12之间互有关联，合成一个模块符合实际情况，主要完成立式分拣机的分拣工作，与实际工作情况一致。零件13,14,15结构互不干扰，功能相互独立，也反映了用户需求和实际操作(13负责开始和结束工作；14可临时暂停工作；15可使暂停的机器重新运转)。1和3虽有联系，但也相互独立，可单独划分。

4 结论

凝聚层次聚类方法是基于底层零件的聚类，能更好地解决零件数量大、结构多而导致计算量大、模块划分过程困难的复杂产品模块划分。

全面考虑产品生命周期各个环节的复杂度，使模块划分对产品生命过程的影响降到最小，基于信息熵理论，为模块划分方案提供了有效的数学评价工具。

实例验证，基于层次聚类的模块划分方法保证了模块之间功能和结构的独立性，同时使模块划分设计变得简单易行。基于信息熵理论的评价方法，综合考虑了模块划分对产品生命周期各阶段的影响，使得最终方案更有利于满足客户的多样化需求，更有利于产品的再设计。