含磁电弹夹层的压电/压磁层合纳米梁弯曲的研究
朱炳任, 刘世伦, 陈红迁
(1. 陆军装甲兵学院车辆工程系, 北京 100072; 2. 陆军装甲兵学院装备保障与再制造系, 北京 100072)
压电和压磁材料及其复合结构因具有优越的力磁和力电耦合性能被广泛应用于便携电子设备的制造中[1]。与其他复合方式相比,压电和压磁材料的层状复合结构在室温下的磁电性能更为突出[2]。尽管诸多研究者对压电和压磁材料的层状结构的力学行为进行了大量研究[3-8],但他们主要关注压电和压磁材料的单层结构或通过理想方式结合的层合结构的力学行为。在工业生产中,热压法是加工PE/PM层状复合材料常用的工艺[9],这种加工方法制得的层合材料会在压电层和压磁层之间形成同时含有2种材料颗粒的夹层,称之为磁电弹(Magneto-Electro-Elastic,MEE)夹层,其同时具有力、电、磁耦合性能[10-11]。在纳米尺度上,该夹层对层合材料的力学性质的影响十分明显[12]。因此,笔者考虑了热压法对层合梁界面层的实际影响,基于正弦剪切型变形梁与非局部理论理论,建立了含MEE夹层的层状复合梁的力学模型,通过哈密顿原理推导出层合梁的平衡方程与边界条件,并分析了MEE夹层对层合梁中点弯曲挠度的影响规律,以期为工程中压电材料和压磁材料的层状复合结构的应用提供理论参考。
1 理论模型
1.1 几何模型
图1为横向载荷qm(x)作用下含磁电弹夹层的压电/压磁层状复合纳米梁理论模型。层状复合纳米梁受简支约束,图中:L、b分别为纳米梁的长度和宽度;h(j)(j=1,2,3)为第j层高度,且有h(1)+h(2)+h(3)=h,h(1)=h(2),h(3)=h0。建立直角坐标系,x轴正方向沿MEE夹层中心线水平向右,z轴沿层合梁的左端垂直向下,y轴方向由右手螺旋法则确定。

图1 横向载荷qm(x)作用下含磁电弹夹层的压电/压磁层状复合纳米梁理论模型
1.2 非局部本构模型
由于层合纳米梁的力学行为存在尺寸效应,为提高计算精度,采用非局部理论来描述其尺寸效应[12]。假设层合纳米梁中应变、磁场强度、电场强度沿纳米梁高度方向连续变化,应力、电位移、磁感应强度沿高度方向的变化不连续[13],层合纳米梁沿z轴极化。因此,压电和压磁材料的非局部本构关系为[14]
(1)
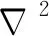
为广义位移,其中εxx和γzx为应变分量,Ex和Ez为电场强度分量,Hx和Hz为磁场强度分量;Λ(j)为本构矩阵,其具体形式为
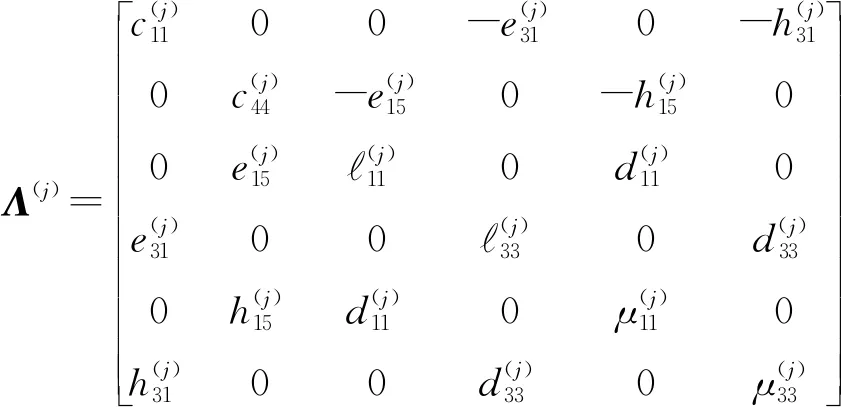

1.3 层合纳米梁模型
采用正弦剪切变形理论对层合纳米梁的弯曲进行分析。电势与磁势的分布满足麦克斯韦方程。基于此,WANG[15]首先假设电势是一个余弦函数加上一个线性函数;此后,这一假设在压电和压磁梁、板的弯曲、屈曲和振动分析中得到了广泛应用[16-17]。在此,也采用上述假设。由于电场与磁场的相关物理量关系式形式相同,因此对磁势也采用相同形式的表达式。层合纳米梁的电势、磁势和横向位移、纵向位移可依次表示为
(2)
式中:φ0(t,x)、ϑ0(t,x)、w0(t,x)、u0(t,x)、ψ0(t,x)分别为层合梁中面的电势、磁势、横向位移、纵向位移以及绕y轴的转角;Δφ、Δϑ分别为层合纳米梁上下表面电势和磁势差,由于层合梁无外加电势,也并不处于磁场之中,因此Δφ=0,Δϑ=0。下标中的逗号表示对相应坐标的偏导数。
层合纳米梁广义的几何关系为
(3)
将式(2)代入式(3)可得
(4)
1.4 载荷模型
在层合纳米梁的上表面沿z轴正方向加载单位面积为qm(x)的横向外力,将其按傅里叶级数展开为
(5)
式中:

(6)
层合纳米梁所受载荷为均布载荷q0,此时
Qn=4q0/(nπ),n=1,3,5,…。
(7)
2 求解运动方程
(8)
因此,广义应力τ(j)所做的虚功为
(9)
式(8)中的广义虚应变δε由式(4)通过变分获得。将式(8)代入式(9)并进行分部积分处理,可得


(10)
式中:
横向力所做虚功

(11)
根据虚功原理可知:广义应力与横向外力所做虚功相同[12]。即

(12)
将式(10)、(11)代入式(12)并化简,即得到层合纳米梁平衡方程
(13)
以及相关边界条件
(14)
为方便求解平衡方程(13),且满足层合纳米梁的边界条件(14),将广义位移u0,w0,φ0,ϑ0和绕y轴的转角ψ0用如下三角级数表示:
(15)
式中:Un、Ψn、Wn、Φn、Θn均为无量纲待定系数。
结合式(1)、(13)、(15),并利用三角函数的正交性对方程组进行化简,可得
(16)

将式(17)化为矩阵方程式的形式,即
PE=Q。
(17)
式中:P为系数矩阵;E=[UnWnΨnΦnΘn]T,Q=[0 -α(4q0/nπ) 0 0 0]T。
3 数值计算与讨论
将层合纳米梁平衡方程赋值,求解平衡方程非零解Wn。通过式(2)、(15)求得层合纳米梁弯曲挠度w,为便于对比分析,将弯曲挠度通过
(18)
进行无量纲化处理
3.1 退化验证计算
为验证本文对层合梁弯曲控制方程的推导是否正确,通过
(19)
将层合梁退化为各向同性单层弹性梁,并按文献[18]的参数设定进行计算,结果见表1。可以看出:本文计算结果与文献[18]一致,证明本文理论推导的正确性。
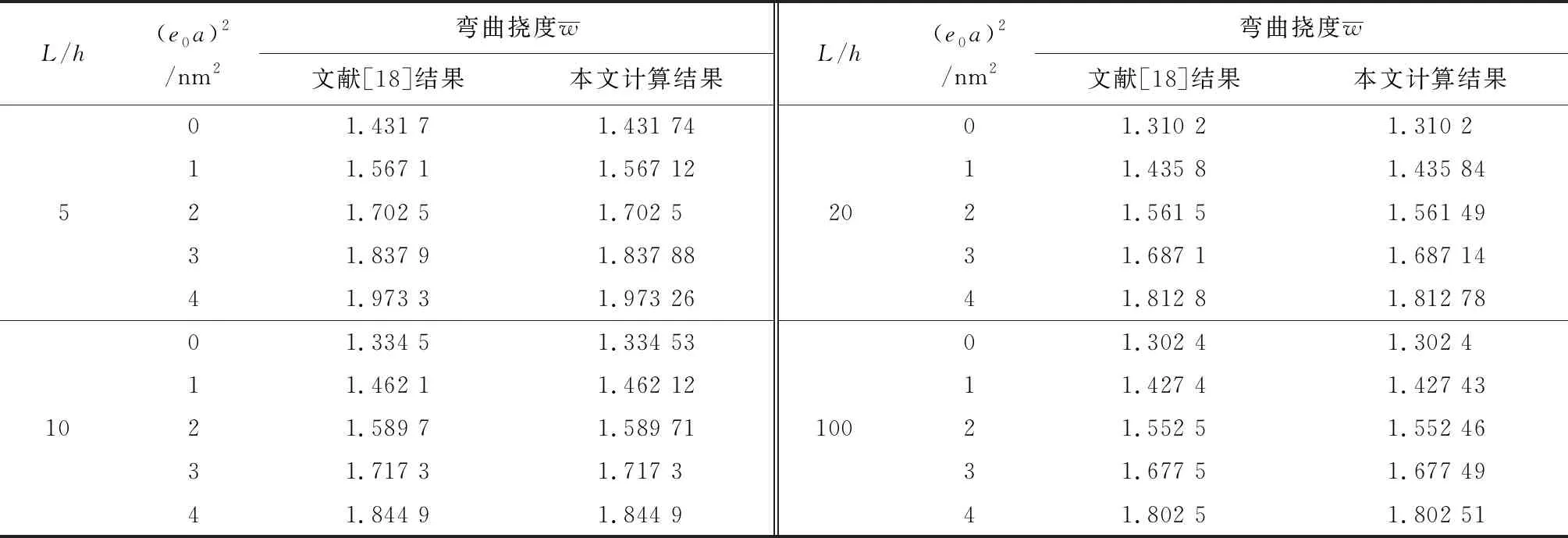
表1 各向同性单层弹性纳米梁无量纲梁中点弯曲挠度
3.2 重要参数对弯曲影响规律
令层合纳米梁长度L=10 nm,长高比L/h=5、7、10式(15)中x=L/2。压电材料选用BaTiO3,压磁材料选用CoFe2O4,相关材料材料参数见表2。
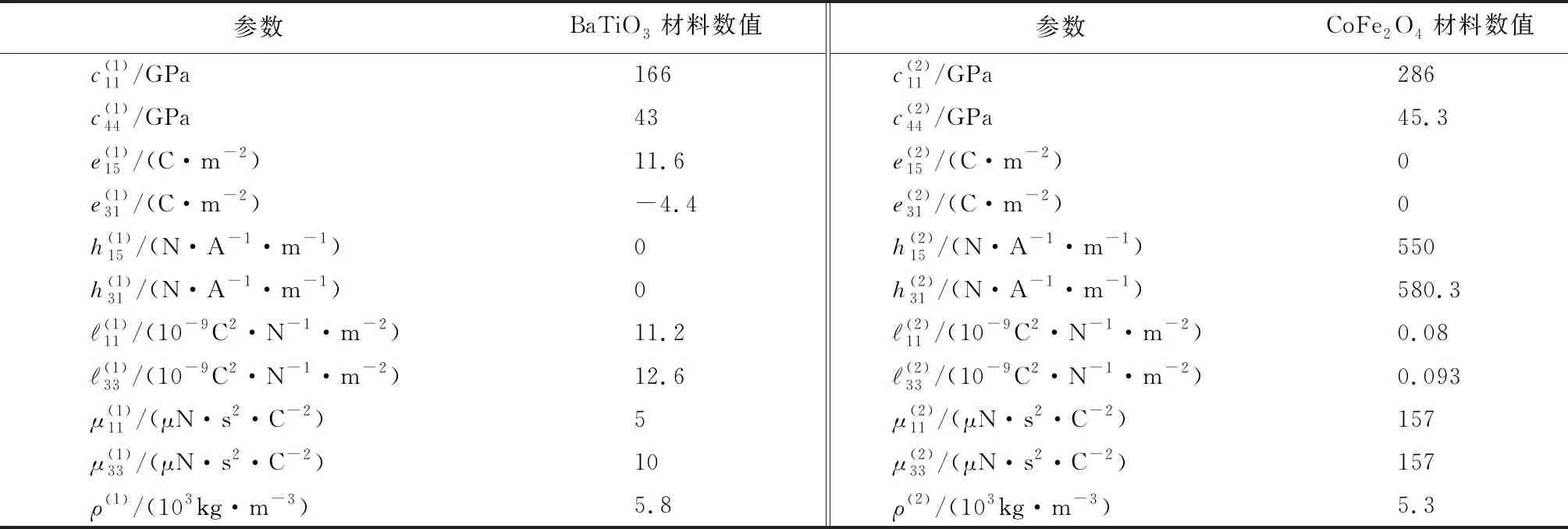
表2 材料参数[19]
根据混合律理论[20],MEE材料的相关材料参数Pmee与压电材料Pe和压磁材料Pm参数满足
Pmee=PeVe+PmVm。
(20)

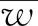

图随Ve的变化曲线
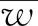
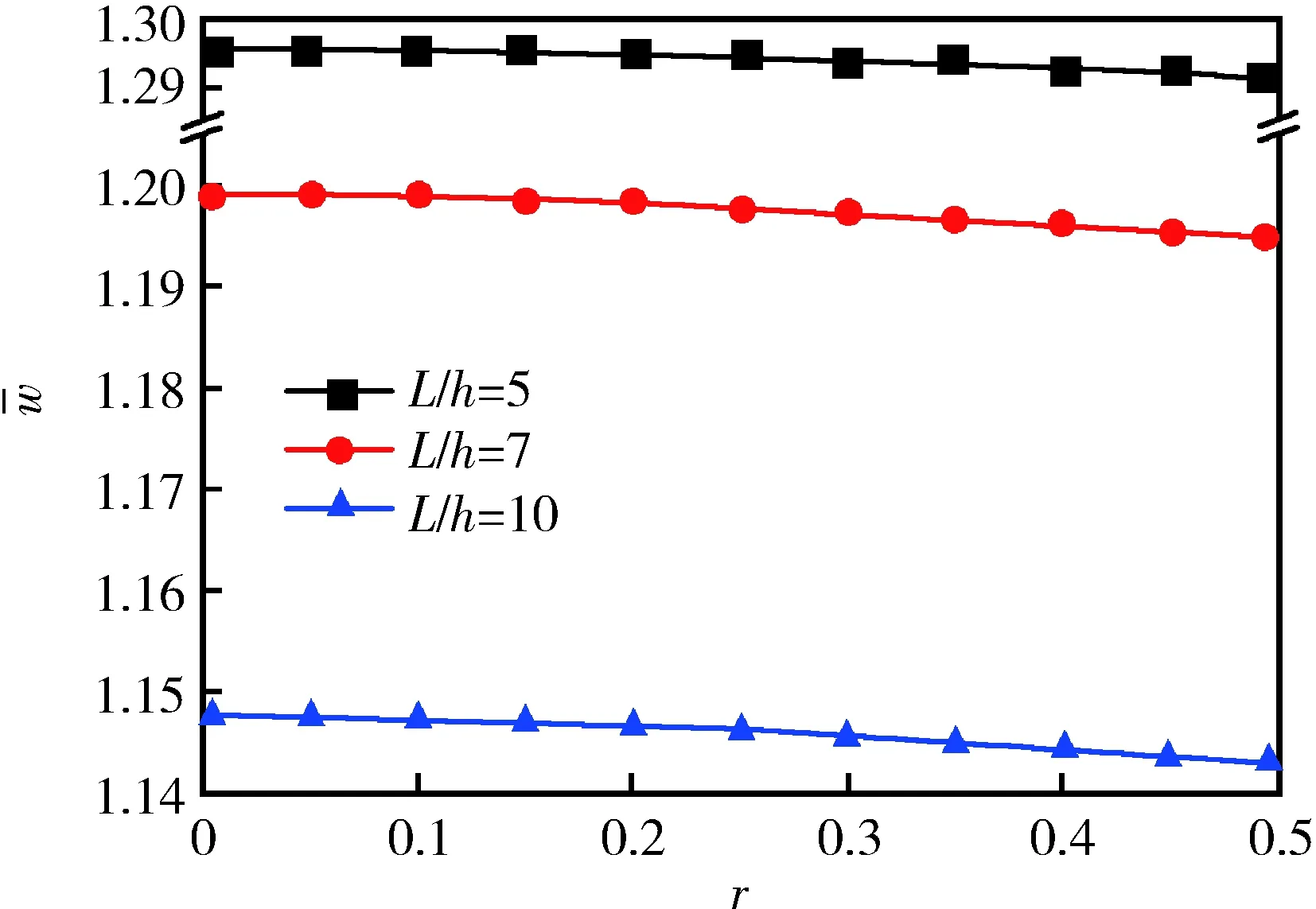
图随r的变化曲线

图随(e0a)2的变化曲线

4 结论
为研究含MEE夹层的PE/PM层状复合纳米梁的弯曲规律,基于非局部理论与正弦剪切型变形梁理论建立了相应力学模型,并应用虚功原理和正弦剪切变形理论推导出层合梁的平衡方程与边界条件,最后通过数值计算,求解出了层合梁中点的弯曲挠度,分析了其随MEE夹层重要参数的变化规律。主要结论如下:
1) 压电材料体积分数和层厚比为磁电弹夹层的重要参数,二者对层合梁抗弯刚度的影响效应互逆:前者对抗弯刚度起弱化作用,后者起强化作用。
2) 压电材料体积分数和层厚比都对层合梁的抗弯刚度的影响效果较为明显,二者均随长高比增大而变明显。
3) 非局部参数对层合梁的抗弯刚度有弱化作用。当长高比变大时,非局部参数对层合梁的弱化作用随之变小。
附录A
βNxx,x、βMxx,xx、βPxx,x、βQzx、βRx,x、βRx,x、βSz、βTx,x、βUz均为控制方程中具有相似形式的表达式,具体形式如下:

(h/π)(nπ/L)2sin(zπ/h)Ψn]+
(A-1)
z(nπ/L)4Wn+(h/π)(nπ/L)3sin(zπ/h)Ψn]-
(A-2)
(nπ/L)2Un+z(nπ/L)3Wn-
(h/π)(nπ/L)2sin(zπ/h)Ψn]+
(A-3)
(A-4)
(A-5)
(nπ/L)Un+z(nπ/L)2Wn-
(h/π)(nπ/L)sin(zπ/h)Ψn]-
(A-6)
(A-7)
(nπ/L)Un+z(nπ/L)2Wn-
(h/π)(nπ/L)sin(zπ/h)Ψn]-
(A-8)

