面向多目标的弹药毁伤试验信息获取M策略研究

史宪铭， 赵汝东， 尤志峰， 姜广胜，2

(1. 陆军工程大学石家庄校区装备指挥与管理系， 河北 石家庄 050003；2. 陆军步兵学院石家庄校区军政基础系， 河北 石家庄 050003)

弹药需求预计是弹药保障的基础性工作，对于弹药筹措、储备、补给都具有基础性牵引作用。为科学预计弹药需求，在仿真计算的基础上，需要对一定数量的弹药进行实装实打试验，而观察次数优化对检验弹药打击效果十分重要。为使数据统计精度最高，打一发进行一次观察统计最为精确，但因受到诸多因素(如目标区域封锁时间、试验时长、试验费用)的制约，则需要在统计精度、试验时间和试验成本之间进行权衡。

以往实装实打试验侧重试验结果忽略过程优化，主要是通过实装实打试验得到弹药的毁伤模式[1]、毁伤能力[2]或打击效能[3]，而对于试验本身优化的研究较少。基于此，笔者在可靠性截尾试验[4-5]统计分析基本原理的基础上，提出了弹药毁伤试验最优信息获取M策略，以得到某弹药对某种目标达到某一毁伤等级时的弹药需求量，最后通过实例对构建的多目标优化模型进行了验证，以期为不同弹药对不同目标毁伤到不同程度下的弹药需求预计提供理论依据和数据支撑。

1 信息获取M策略

1.1 基本原理

信息获取M策略，是指弹药毁伤试验中对统计精度、试验时间和试验成本进行权衡得到的策略。标准弹药间隔发数下的信息获取策略，是指在进行弹药毁伤试验时，为准确评估毁伤程度、测定目标毁伤等级而采取的打一发弹药现地观测一次毁伤效果的方案，简称“标准试验”，此时策略M=1。信息获取M策略结合了可靠性截尾试验统计分析的基本原理，其基本思路为：在目标装备完好率为100%的前提下，以标准弹药间隔发数打击目标装备，并观察统计目标毁伤情况，如此往复进行，直到目标达到特定的毁伤等级时停止射击，记录达到该毁伤等级的弹药量。

1.2 弹药需求量分析

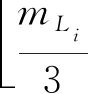
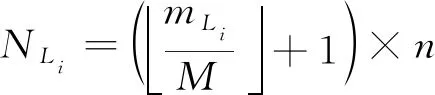
(1)

式中：⎣·」为向下取整函数。

1.3 M策略考虑因素分析

以标准弹药间隔发数进行弹药毁伤试验，可以及时准确地观测到每打完一发弹药目标作战效能的变化情况，最真实地反馈目标的毁伤程度，使得测定的试验数据精确度最高。虽然统计精度为非常重要的指标，但从试验整体出发仍需考虑经济、时间等因素，以保证弹药毁伤试验的可行性。

2 多目标参数分析

2.1 弹药毁伤试验时间

弹药毁伤试验时间T包括试验准备时间Tpr、单发弹药飞行时间Taf、试验数据采集耗时Tdc等，反映了毁伤试验的效率，其表达式为

(2)

2.2 弹药毁伤试验费用

弹药毁伤试验总耗费C包括[6]单发弹药费用Cam、试验材料费Ctm、人员成本Cst、单个目标装备费用Cte。其中：Cam为单发弹药价值与毁伤试验过程中发射1发弹药所需的其他费用的总和；Ctm为试验过程中所需的传感器、标记物、油料等易耗品的成本，该项费用与观测次数直接相关；Cst为试验人员的各项开支，包括工资补贴、生活开支及其他费用，是试验时间的函数；Cte为承受毁伤试验的单个废旧装备或产品样本所具有的价值。则有

(3)

2.3 毁伤效果统计精度

为计算方便，用不同信息获取方案下各目标达到毁伤等级Li时的均值与标准试验下均值的相对误差来表示统计精度，相对误差越小，则精度越高。

目标毁伤等级是按毁伤程度对目标的毁伤程度划分的级别。参考文献[7]将目标毁伤划分为5种等级，如表1所示。因零毁伤基本不影响打击目标的作战效能，且毁伤试验中此情形发生的可能性极小，故不对目标零毁伤时的弹药量展开研究。

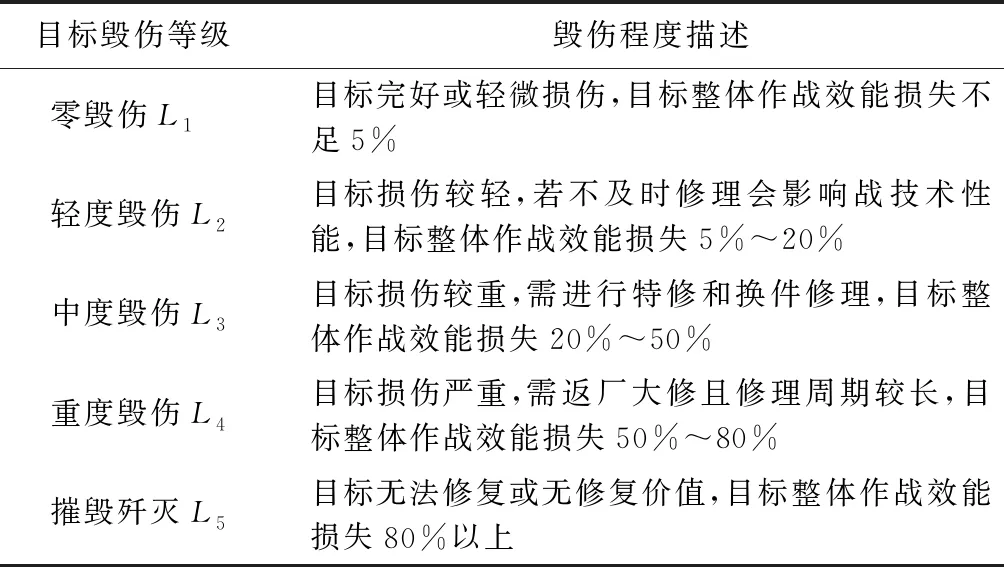
表1 目标毁伤等级界定

毁伤试验往往设置多个目标，已知标准试验中各目标达到毁伤等级Li时的弹药需求量均值为μ，则间隔发数为n时每个目标达到毁伤等级Li的弹药需求量均值和标准差可依次表示为[8]

(4)

(5)

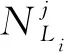
由于弹药价值高，试验次数较少，故采用t分布检验原理[9-10]对误差进行统计分析，即

(6)

式中：tγ为t分布概率密度函对应的随机变量。

对式(6)移项可得

(7)

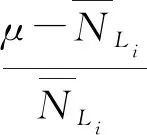
(8)

由式(8)可得

(9)

取置信度γn=95%，结合式(9)并查找t分布表计算tγ，从而获取δn的值。

δn为间隔发数n时的统计误差，未充分体现由于间隔发数选取带来的误差。经研究，当间隔发数为n时，每个目标达到毁伤等级Li的弹药需求量标准差与间隔发数为正相关。为便于研究，取n=1时的s′代替sn，取间隔发数M作为调节系数，此时相对误差δ可表示为

(10)

3 模型构建及求解

3.1 基本假设

为了简化问题，突出研究重点，做如下假设：

1) 当间隔发数为n时，每个目标达到毁伤等级Li时的弹药需求量的均值，为此方案下的实际弹药需求量；

2) 当敌方作战效能损失80%以上，不再具备反击能力时，意味着目标已被歼灭，此时停止射击，所提供弹药足以摧毁目标；

3) 弹药毁伤试验不考虑敌方目标对我方的反击，我方装备始终处于完备可持续战斗状态；

4) 当目标装备为同种装备时，其战术技术性能相差不大，且达到特定毁伤等级所需弹药量也相差不大；

5) 弹药发射间隔期忽略不计，只统计单发弹药从开始射击到命中目标所用的时间；

6) 工作人员每次观测目标装备毁伤程度所用时间不因其毁伤程度的差异而不同；

7) 当目标装备有50%及以上毁伤等级达到Li时，即可认定此时毁伤等级为Li。

3.2 约束条件确定

3.2.1 试验时间限制

由于射击时间远远小于观测时间，且毁伤试验要求在一定时间Tlim内完成，则有

试验时间上限

T≤min{Tpr+mLi(Taf+Tdc),Tlim}；

(11)

试验时间下限(一次性打完恰好达到预定毁伤程度)

T≥Tpr+NLiTaf+Tdc。

(12)

3.2.2 试验成本限制

试验毁伤试验费用要在预算以内，即

C≤Cbud。

(13)

费用总额不小于一次标准试验的费用，即

(14)

达到毁伤等级Li+1的弹药需求量大于达到Li级毁伤的弹药需求量，即

Cam(NLi+1-NLi)>0。

(15)

3.2.3 误差区间

根据统计分析，可以确定误差范围为

(16)

3.3 理想点法

为克服不同类型数据的数量级对理想点法目标函数(总目标)的影响，更为客观地体现毁伤试验总时间、试验过程总费用、观测结果误差等3个目标对总目标的贡献，在此对原始的理想点法总目标进行调整，即

(17)

3.4 优化模型建立

在分析毁伤试验总时间、试验过程总费用、观测结果置信度等多个目标的基础上，结合弹药毁伤试验实际，考虑毁伤试验成本限制、精确度范围、时间限定等约束，构建的多目标优化模型[13-18]为

(18)

(19)

(20)

(21)

3.5 算法流程

模型求解算法的具体步骤如下：

1) 设置目标参数，确定各目标表达式；

2) 建立约束条件，确定各变量的取值范围及其数量关系；

3) 构建多目标决策模型；

4) 在各变量取值范围内，搜索其最优点，并输出单目标最优结果；

5) 建立多目标向量函数，定义一定的模，用理想点法求解最优值。

6) 停止运算，输出最优间隔发数及弹药量。

4 实例分析

选取某新型压制武器弹药A作为研究对象，确定目标装备Ek达到中度毁伤L3时的最佳间隔发数及所需弹药量。

假设：试验开始时间为0 h，Tlim=150 h，Tpr=16 h，Taf=0.05 h，Tdc=0.5 h；N=6；Cte=50万元，Cam=20万元，Ctm=5万元，Cst=3万元，Cbud=4 000万元。

表2为装备Ek为不同打击强度下的毁伤率对比。以装备Ek中度毁伤L3为例，通过表2可以看出：当L3>50%时,方可确定目标装备Ek为中度毁伤；当目标装备Ek达到中度毁伤L3时，间隔发数1、2、3分别对应的弹药需求量为84、93、102。

表2 装备Ek不同打击强度下的毁伤率对比

表3为达到中度毁伤时各目标装备所需弹药量。根据表3中不同间隔发数下的弹药需求量可以确定标准试验中：μ=14，s′=0.83；当置信度γn=95%、N=6时，tγ=2.446 9。根据式(17)、(21)可以确定多目标下最佳弹药间隔发数为1.3发，需求弹药14.3发。

表3 达到中度毁伤时各目标装备所需弹药量

表4为标准试验与信息获取最佳策略数据对比。可以看出：在保证信息获取最佳策略统计精度在90%以上的基础上，与标准试验相比，信息获取最佳策略降低了成本、节约了时间。按照理想点法得到的不同毁伤等级要求下弹药打击目标时的信息获取M策略及各方案下的弹药需求量，如表5所示。

表4 标准试验与信息获取最佳策略数据对比

表5 信息获取M策略及各方案下的弹药需求量 发

5 结论

当前针对弹药毁伤试验数据采集方案设计的研究较少，以毁伤试验最佳弹药间隔发数的选取为目标展开研究，在试验成本限制、精确度范围、时间限定等约束下构建起考虑毁伤试验时间、试验过程费用、统计精度等多个目标的优化模型，确定了信息获取最佳策略和弹药需求量。实例表明：借助t分布检验原理统计分析各方案下的误差，用不同信息获取方案下各目标达到毁伤等级Li时的均值与标准试验下均值的相对误差来表示统计精度，可为今后基于统计推断的弹药需求预计精度测算提供思路；采用理想点法目标函数，在一定程度上降低了主观性，克服了不同类型数据的数量级对目标函数的影响；模型及算法科学、可行，能够指导弹药毁伤试验信息获取工作。

为更精确地确定达到各毁伤等级的弹药需求量，下一步可以融合专家经验数据、试验仿真数据等先验信息，借助贝叶斯推断、D-S证据理论等融合方法确定弹药需求量，以达到弹药精确保障的目的。