蔡氏电路的实验与仿真研究

吴淑花，孟玮德，马志春

（石家庄学院 机电学院，河北 石家庄 050035）

0 引言

自混沌运动于1963年被美国气象学家Lorenz首次发现以来[1]，混沌理论及其相关应用在50多年里被不断地深入挖掘，从医学上对于癫痫病的预报，到野生动物种群的数目消长，再到长期准确的天气预报、保密通信以及天体轨道的预测，混沌的身影无处不在.混沌电路是研究混沌理论的重要手段之一，自1983年蔡少棠发表蔡氏电路以来[2-7]，以实际应用为主的蔡氏电路改进、变形、多涡卷蔡氏电路及基于忆阻器的混沌系统等相关研究层出不穷，而且应用于更广泛的领域[8-18].例如，文献[9]充分利用放大器本身限幅的非线性特点构造蔡氏等效电路，删除了电感这一使电路性能不稳定的元件，让电路结构简单、误差小并且易于调节，适用于保密通信；文献[11]提出一种模块化设计方法，由三涡卷蔡氏无量纲状态方程设计电路，仅使用了反相加法器、积分器和反向器构成电路，使各元件参数独立可调，易于电路实现；文献[13]简化双运放型蔡氏电路，并验证其确实可以产生混沌信号，降低了研究成本.

蔡氏电路在混沌研究中占有重要地位.本研究利用以蔡氏电路为原理的ZKY-HD实验仪进行相关实验研究，探究非线性电阻RNL的工作原理，并通过示波器观察变阻器W1阻值变化对混沌相图的影响，分析W1在电路中所承担的作用.同时利用Multisim对实验仪的构成电路进行仿真，观察电感L1和变阻器W1的参数变化对混沌相图的影响，并搭建仿真电路测量非线性电阻RNL的伏安特性.将仿真结果与实验结果对比，分析得出ZKY-HD实验仪各模块元器件的职能，进而帮助初学者理解蔡氏电路的工作原理.

1 ZKY-HD实验仪的结构与原理

1.1 ZKY-HD实验仪的构成

ZKY-HD型混沌原理及应用实验仪（6303）由成都世纪中科仪器有限公司生产，仪器机号为07-007，其结构图如图1所示.ZKY-HD实验仪的电路图如图2所示，仪器参数（混沌信号发生模组）为：L1=18 mH，C1=100 nF，C2=10 nF，R1=3.3 kΩ，R2=22 kΩ，R3=22 kΩ，R4=2.2 kΩ，R5=220 Ω，R6=220 Ω.

图1 ZKY-HD实验仪结构图

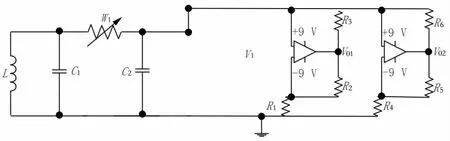
图2 ZKY-HD实验仪元件构造图

1.2 蔡氏电路

蔡氏电路是1983年由美籍菲律宾华裔蔡少棠搭建的一种非线性电子电路，它能够表现出完整的混沌分岔和混沌吸引子行为，并且容易实现.蔡氏电路主要由非线性电阻、变阻器、电感以及电容所构成[2-5].其原理如图3所示，其中RNL为非线性电阻.图4即是一种简单的非线性电阻的实现方式.

2 利用ZKY-HD实验仪的实验研究

以下通过实验探究W1、RNL模块在混沌信号的产生中对电路的影响.先将非线性电阻RNL作为独立模块，实验研究该模块的伏安特性；再将W1放在整个电路里，保持其他元件参数不变，调节W1的大小观察系统的状态变化，以此来研究可变电阻的大小对系统的影响.

2.1 对RNL的实验研究

一般情况下，电阻是作为负载的角色参与电路构成，电阻两端的电压大小与通过电阻的电流大小成正比，作伏安特性曲线其斜率为正，通常被称为正阻；若电阻两端的电压大小与通过电阻的电流大小成反比，斜率为负，这样的电阻即为负阻.自然界中不存在天然的负阻元件，只有电阻处于电路中且有电流通过才会有负阻产生.负阻代表电阻在电路中发挥电源的作用，而正阻是电阻的本质属性.从功率意义上来说，正阻是耗能元件，负阻输出功率，是产能元件，可视作电路中的电源.

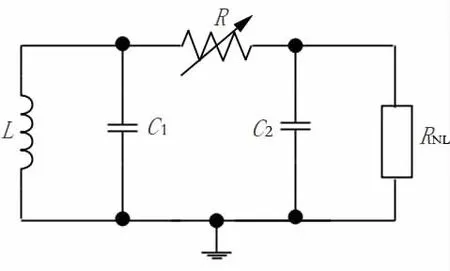
图3 蔡氏电路原理图

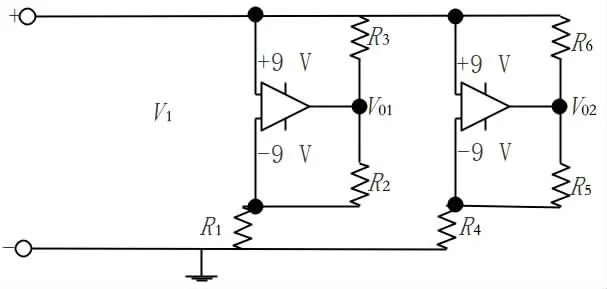
图4 非线性电阻

RNL模块内部构成如图4所示，通过改变电源电压，测得多组数据，利用这些数据作I-U曲线如图5所示.

由I-U伏安特性曲线可得：当|V1|≤|VC|时，在I-U图中的CD段，两个运放均为正常工作，由于运放输入端不取电流，且对于该同相加法器存在虚断和虚短，则有[2]：

即：

解得：

而 R3=R2，R6=R5，代入数值得 kCD≈-0.76×10-3，从表格数值看 kCD≈-0.7×10-3.

当|VC|≤|V1|≤|VB|，在I-U图中的BC和DE段，左侧的运放单元输入电阻大，先到达饱和，不承担放大作用，其作用仅相当于电阻和一个电源串联，即R3以用电器的身份接入电路，而右侧运放单元依旧工作在放大区，则此时[2]：

代入数值得 kBC≈-0.41×10-3，从表格数值看 kBC≈-0.4×10-3.

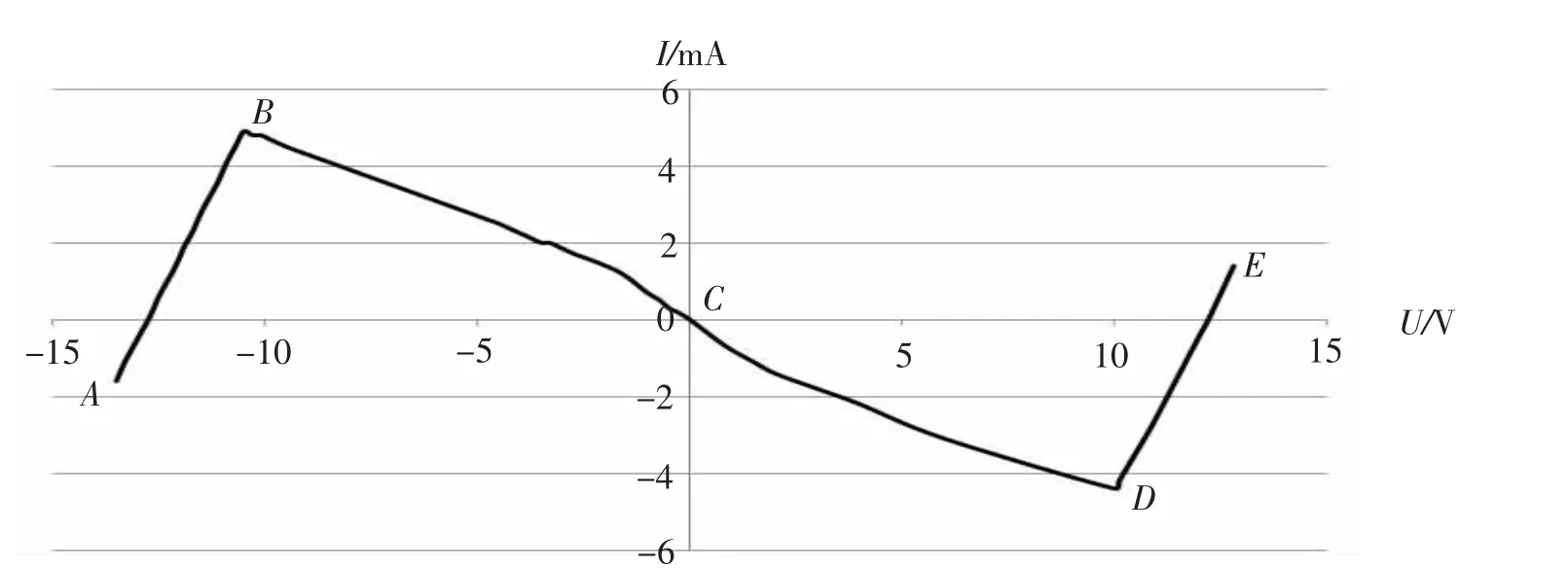
图5 RNL的I-U曲线

当|VB|≤|V1|，在I-U图中的AB和EF段，两组运放单元全部达到饱和，R3、R6以用电器的身份接入电路，此时[2]：

代入数值得R总≈4.59×10-3Ω，从表格数值看kAB≈2.3×10-3.

在可变电压源取不同电压值时，RNL所得阻值也不同，其I-U伏安特性曲线表现为5段线性函数.可见，RNL的作用一是维持LC振荡电路的振荡信号；二是使得振荡周期产生分岔与混沌等一系列非线性现象.

2.2 对W1的实验研究

W1为变阻器，当将W1扭旋到底时，即阻值为零时其相图为一个点，也就是说，此时电路系统处于平衡点；慢慢调节W1，使其阻值逐渐增加，电路状态依次为单周期、双周期、4周期、多周期直至单吸引子和双吸引子.随W1增大示波器输出的相图如图6所示.

通过电路实验可知，当W1阻值为零时混沌相图为一点，随着其阻值的增加，系统状态展示出完整的倍周期分岔过程，并在增大到一定值时电路进入混沌振荡状态，但由于该实验仪无法读出W1阻值，因此对于周期分岔和混沌吸引子的分界线无法知晓，利用Multisim仿真可以测得数值.

3 基于Multisim的电路仿真研究

利用Multisim对ZKY-HD实验仪的原理电路进行仿真，电路搭建如图7所示，通过改变L1和W1的元件参数，探究其对电路的影响.

3.1 L1的参数变化对电路的影响

系统元件参数分别为 L1=18 mH，C1=100 nF，C2=10 nF，R1=3.3 kΩ，R2=22 kΩ，R3=22 kΩ，R4=2.2 kΩ，R5=220 Ω，R6=220 Ω.保持其他元件参数不变，仅改变电感L1的大小，观察系统的状态变化.具体取值范围见图8，该图为电路系统的相图变化.

通过对以上数据分析，当0mH≤L1＜12.27 mH时，混沌相图为一点，即此时系统处于平衡点；在12.27 mH≤L1＜15.89 mH范围内，电路系统随着电感数值的增大展示出完整的倍周期分岔过程；当15.89 mH≤L1＜23.3 mH时，电路系统处于混沌状态.L1作为振荡信号产生的一部分，其数值选择不同，系统非线性振荡的程度也不同，随着电感的增大，对电路系统非线性振荡影响越强，系统越容易进入混沌状态.

图 6 电路系统的相图.（a）单周期分岔；（b）双周期分岔；（c）4 周期分岔；（d）多周期分岔；（e）单吸引子；（f）双吸引子

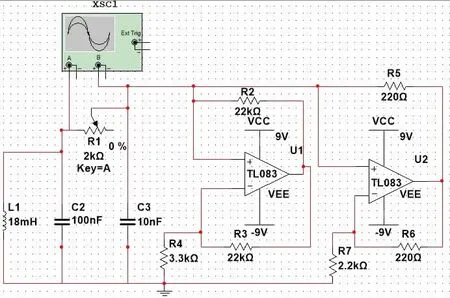
图7 ZKY-HD实验仪的电路仿真

图 8 电路系统的相图.（a）12.27 mH≤L1＜14.57 mH；（b）14.57 mH≤L1＜15.22 mH；（c）15.22 mH≤L1＜15.29 mH；（d）15.29 mH≤L1＜15.89 mH；（e）15.89 mH≤L1＜16.23 mH；（f）16.23 mH≤L1＜23.3 mH

3.2 W1的参数变化对电路的影响

系统元件参数为 L1=18 mH，C1=100 nF，C2=10 nF，R1=3.3 kΩ，R2=22 kΩ，R3=22 kΩ，R4=2.2 kΩ，R5=220 Ω，R6=220 Ω，保持元件参数不变，仅改变变阻器W1的大小，观察系统的状态变化，具体取值范围见图9，该图为电路系统的相图变化.

通过仿真数据分析，当0 Ω≤W1＜8 Ω时，混沌相图为一点，电路处于平衡状态；随着电阻大小的增加，在8 Ω≤W1＜86 Ω范围内，系统状态展示出完整的倍周期分岔过程；当86 Ω≤W1＜492 Ω时，系统处于混沌振荡状态.仿真结果与实验测得结果相吻合，并确定了具体的阻值范围及周期分岔及混沌吸引子的分界线.将电路实验与仿真实验结合分析，W1将非线性电阻与LC振荡电路的特性相融合，促使电路系统处于非线性振荡状态，随着阻值增大，其影响越大.

3.3 RNL的伏安特性

利用Multisim搭建非线性电阻的仿真电路，探究其伏安特性，仿真电路如图10所示，所得I-U仿真曲线如图11所示.

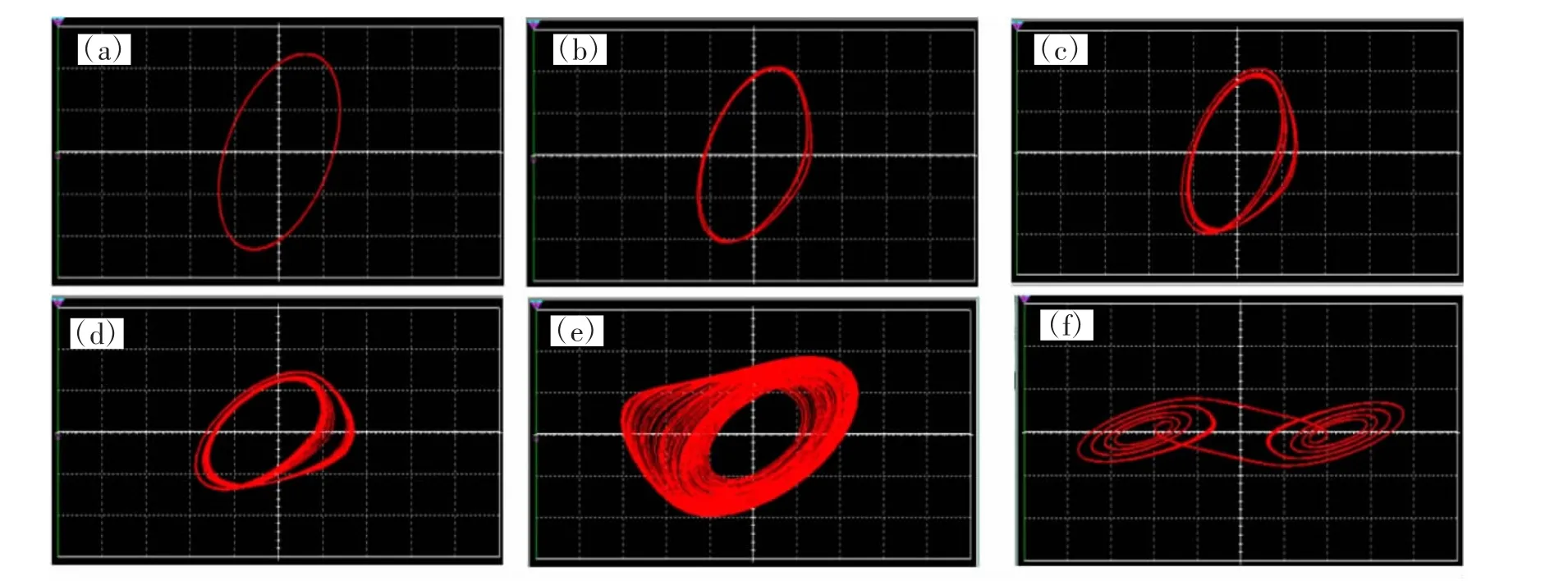
图 9 电路系统的相图.（a）8 Ω≤W1＜58 Ω；（b）58 Ω≤W1＜72.6 Ω；（c）72.6 Ω≤W1＜76 Ω；（d）76 Ω≤W1＜86 Ω；（e）86 Ω≤W1＜112 Ω；（f）112 Ω≤W1＜492 Ω

仿真电路搭建说明：1）XFG1为函数发生器，选择信号为三角波，振幅选择为15 V，选择三角波信号中电压随时间增大时段，令其作为-15 V到+15 V线性变化的正比例函数信号源；2）在Multisim中，为了将电流测量转化为电压测量，外接一个阻值为1 Ω的电阻，测得电阻两端的电压即为通过电路干路的总电流，由示波器XSC1直接显示伏安特性曲线，如图11所示.

从结果中可以看到明显的5段线性函数，再一次验证了RNL的非线性.与图6对比可见，电路实验与仿真研究相互验证.由于仿真电路更理想化，所以其伏安特性曲线为分段线性函数的结果更清晰，转折点也更明显.

4 结论

在蔡氏电路中，各元件参数的变化都会对电路系统产生影响.本研究在通过电路实验研究的同时，利用Multisim对实验仪的构成电路进行仿真实验，将两种实验研究相互对比分析，探究可调电阻W1、非线性电阻RNL以及电感L1的电路职能.

通过以上两种实验方式的结果，分析电感和变阻器的数值对混沌相图的影响，发现电感元件和可变电阻对系统的影响很相似：随着电感参数（或变阻器阻值）的增大，系统由平衡点进入到倍周期分岔，进而进入混沌状态，也就是说足够大的电感和可变电阻保障了电路的非线性振荡，其正确性被Multisim仿真结果所证实.仿真电路对非线性电阻伏安特性的测量直观地展现出其I-U仿真曲线为5段线性函数，进一步验证了电路实验结果的正确性.

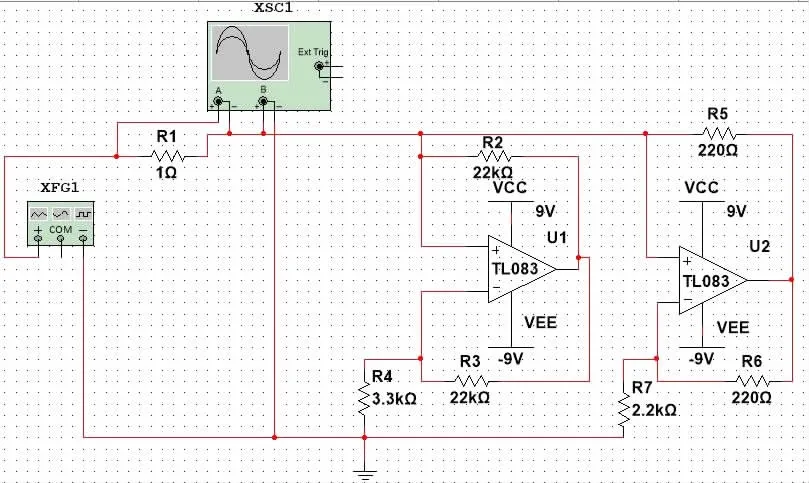
图10 RNL仿真电路图

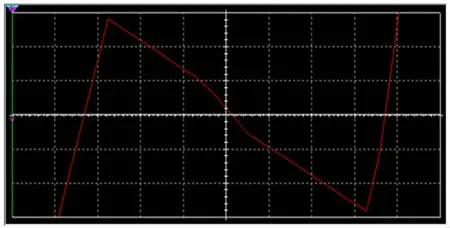
图11 I-U仿真曲线图

本研究可以帮助初学者快速掌握蔡氏电路的工作原理，理解各模块元器件的职能，并为蔡氏电路的改进与优化提供理论支持.