基于3次Bezier曲线的缓冲包装CAD框架构建*

徐绍虎， 崔 爽

(重庆工商大学 机械工程学院，重庆 400067)

0 引 言

为了提高缓冲包装设计的效率，很多学者进行了缓冲包装CAD系统的开发研究。戴杰明[1]等用Delphi开发了缓冲包装CAD系统；田丽[2]等、李光[3]等以Visual Basic为编程语言，开发了缓冲包装CAD 系统；黄颖为[4]等、袁艳[5]等以Visual C++为编程语言，开发了缓冲包装CAD 系统；卢杰[6]等用C++Builder开发了缓冲包装CAD 系统。缓冲系数—最大应力曲线经常被用于缓冲包装设计。缓冲材料不同，其缓冲系数—最大应力曲线也不同。目前，在进行缓冲包装设计时，往往需要根据缓冲系数—最大应力曲线来确定缓冲衬垫的面积和厚度。其实，如果缓冲系数—最大应力曲线方程已知，那么只需根据方程来设计即可。然而，由于缓冲材料的静态压缩本构模型多是非线性的，故其应力—应变曲线方程很难用确定的数学关系式来表达；即使采用数值分析的方法进行拟合，在分段表示本构模型时容易出现不易收敛的问题[7]。而缓冲系数—最大应力曲线是基于缓冲材料的静态压缩试验得到的，同样很难用确定的数学关系式来表达其方程；即使根据拟合的本构模型来推导，得到的缓冲系数—最大应力曲线方程类型也各不相同。这样，在利用计算机进行辅助缓冲包装设计时很难用统一的方法来处理以获得缓冲衬垫的尺寸。曾在文献[8]中提出了利用3次Bezier曲线建立基于静态压缩试验的蜂窝纸板本构模型，得到的拟合曲线和实验曲线有很好的拟合度，方法可以推广至建立所有缓冲材料的本构模型，进而得到缓冲系数—最大应力参数方程。基于3次Bezier曲线，提出了利用计算机辅助缓冲包装设计流程，并探讨了确定缓冲衬垫尺寸的软件开发框架设计。

1 3次Bezier曲线[9]

Bezier曲线由一组多边折线(称为特征多边形)的顶点唯一控制其形状，n次Bezier曲线需n+1个控制点。Bezier曲线经过首末两个控制点，与特征多边形的首、末两条边相切，切点分别为首、末两个控制点。贝塞尔曲线的参数方程可表示为

(1)

式(1)中，Pi(i=0，1，…，n)是特征多边形各顶点坐标，Bi，n(t)是基函数，Bi，n(t)的参数方程可表示为

(2)

一条3次Bezier曲线由点P0(ε0，σ0)、点P1(ε1，σ1)、点P2(ε2，σ2)和点P3(ε3，σ3)4个控制点唯一地定义，如图1所示，点P0和点P3为其首末两点，边P0P1和边P2P3为其切线且切点分别为点P0和点P3，参数方程为

P(t)=(1-t)3P0+
3(1-t)2tP1+3(1-t)t2P2+t3P3(0≤t≤1)

(3)

图1 三次贝塞尔曲线Fig.1 Three cubed Bezier curve

3次Bezier曲线可用分量表示，参数方程按t的升幂排列为

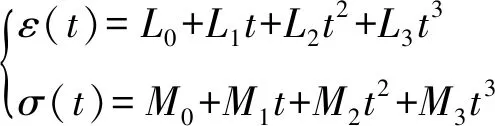
(4)

式(4)中：

L0=ε0L1=-3(ε0-ε1)L2=3(ε0-2ε1+ε2)
L3=-ε0+3(ε1-ε2)+ε3
M0=σ0M1=-3(σ0-σ1)M2=3(σ0-2σ1+σ2)
M3=-σ0+3(σ1-σ2)+σ3

2 缓冲包装设计流程

从缓冲材料试验开始至缓冲包装设计结束，基于3次Bezier曲线的计算机辅助缓冲包装设计流程如图2所示。方法主要包含两个过程：确定缓冲材料的本构模型和缓冲特性曲线参数方程；利用缓冲系数—最大应力曲线进行缓冲包装设计。

图2 基于3次Bezier曲线的缓冲包装设计流程Fig.2 Cushioning packaging design process based on three cubed Bezier curve

2.1 本构模型及缓冲曲线参数方程的确定

读取缓冲材料静态压缩试验数据，绘制应力-应变试验曲线。根据试验曲线的特点，采用3次Bezier曲线分段拟合试验曲线，得到拟合曲线的参数方程。分段点确定的方法根据试验曲线各点切线的斜率变化趋势确定。即：若斜率一直在增大，在某点突然变小，则该点为分段点；反之，亦是。分段点不宜太多(太多的话，可以增大试验曲线的取样点间隔)，原则上不要超过3个，即拟合曲线方程最多采用四段式。

N(N=0，1，2，3)个分段点将实验曲线分成N+1段，每段试验曲线均采用3次Bezier曲线进行拟合。拟合时需要4个控制点，首末两个控制点(点P0和点P3)是已知的，所以需要确定的是另两个控制点(点P1和点P2)。点P1和点P2可采用方法确定：(1) 若试验曲线在由点P0、点P1、点P2和点P3控制的曲线下方，则应将点P1和点P2下移，相反则上移；(2) 若试验曲线谷底开口比由点P0、点P1、点P2和点P3控制的曲线大，那么应该将点P1和点P2的距离增大，相反则减小；(3) 若试验曲线有很长一段斜率变化很小，则由点P0、点P1、点P2和点P3的曲线某条边(相邻控制点的连线)很长，相反则很短。

点P1和点P2确定后，3次Bezier曲线也就唯一地被确定，通过总偏差φ比较拟合曲线和试验曲线的拟合度，总偏差φ的表达式[9]如式(5)所示。

(5)

式(5)中：n为试验曲线取样点的数目；σi为试验曲线第i个取样点的应力值；σ(ti)为对应第i个取样点应力的3次Bezier曲线拟合值。

当φ小于设定的阈值α时，拟合曲线和试验曲线的拟合度好，从而得到3次Bezier曲线拟合的应力-应变参数方程。根据式(6)分段推导出缓冲系数C的参数方程，结合应力-应变参数方程，得到缓冲系数—最大应力参数方程。

(6)

2.2 缓冲包装设计[10]

进行缓冲包装设计时，只要知道W(产品重量)或S(产品表面积)、H(等效跌落高度)、G(产品脆值)，利用缓冲系数—最大应力参数方程就可以得到缓冲衬垫的面积A和厚度T。全面缓冲设计时，缓冲衬垫面积A=产品表面积S，厚度T由式(7)求出。局部缓冲设计时，考虑到外包装的尺寸及缓冲效率，找到选定的缓冲材料最小缓冲系数C及其对应的最大应力σm，由式(7)和式(8)分别求出缓冲衬垫厚度T和面积A。

(7)

(8)

缓冲衬垫尺寸设计完成后，进行衬垫尺寸校核，包括产品强度校核、挠度校核、跌落姿态改变时缓冲能力的校核、蠕变量校核和温湿度校核。

3 软件开发框架设计

3.1 菜单设计

若缓冲材料的缓冲系数—最大应力曲线已知，即已经利用3次Bezier曲线建立了缓冲材料的缓冲系数—最大应力参数方程，则可根据参数方程直接进行设计；若是新材料，则首先需要利用3次Bezier曲线建立该缓冲材料的缓冲系数—最大应力参数方程，将缓冲材料转为已有材料，然后进行缓冲设计。利用Visual Basic进行软件开发时可在窗体(假定命名为Form1)内设计如图3所示的3级菜单。

图3 缓冲材料选择3级菜单设计Fig.3 Three-level menu design for selection of cushioning material

3.2 基于已有材料的控件设计

利用已有材料进行缓冲设计，控件ComboBox设计如图4所示。

图4 缓冲形式选择控件设计Fig.4 Control design for selection of buffer form

以局部缓冲为例，控件Frame、控件Label、控件TextBox、控件CommandButton设计如图5所示。只需输入H、G、W的值，就可以计算出缓冲衬垫尺寸。单击“衬垫尺寸校核”，弹出窗体(假定命名为Form2)，在窗体Form2内进行校核。以挠度校核为例，若A>(1.33T)2，则提示挠度校核通过。

图5 局部缓冲控件设计Fig.5 Control design for partial buffer

3.3 基于新材料的控件设计

需要将新材料转为已有材料。根据新材料的静态压缩试验，得到其应力—应变试验曲线，利用前述方法确定分段点，控件ComboBox设计如图6所示。

图6 曲线拟合段数选择控件设计Fig.6 Control design for selection of number of curve fitting segments

如果试验曲线只利用一条3次Bezier曲线来拟合，则选择“未分段”，控件Frame、控件Label、控件TextBox、控件Command-Button设计如图7所示。点P0和点P3是试验曲线的起点和终点，根据试验曲线先输入点P1和P2的估计值，单击“比较拟合度”，计算φ，并会在控件PictureBox内绘制试验曲线和拟合曲线的比较图，利用前述方法确定点P1和点P2。当φ<α时，拟合曲线和试验曲线的拟合度好，输出参数方程。

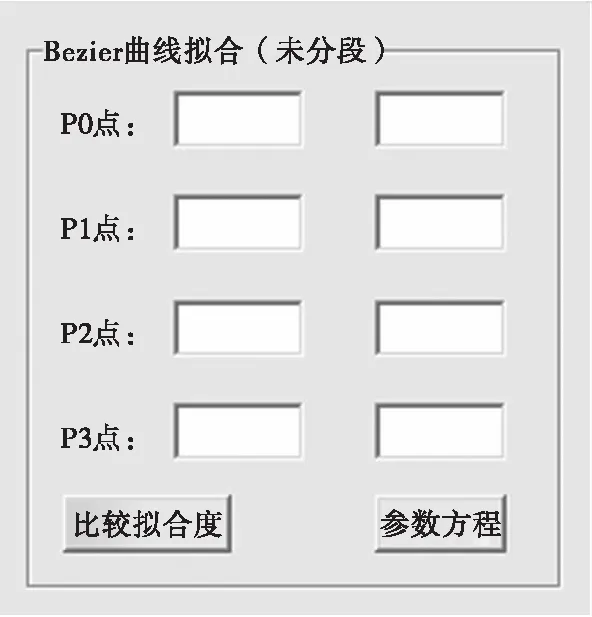
图7 未分段曲线拟合控件设计Fig.7 Control design for unsectioned curve fitting

图8 两段式曲线拟合控件设计Fig.8 Control design for two-stage curve fitting

若试验曲线利用3次Bezier曲线分段来拟合，则根据段数选择“两段式”、“三段式”或“四段式”。以“两段式”为例，控件Frame、控件Label、控件TextBox、控件CommandButton设计如图8所示。第一段中，点P10是试验曲线的起点，点P13是分段点，根据试验曲线先输入点P11和点P12的估计值，“比较拟合度”和“参数方程”操作同前，单击“下一段”，进入第二段。第二段中，点P20是分段点，点P23是试验曲线的终点，根据试验曲线先输入点P21和点P22的估计值，后面的操作同前。

根据得到的应力—应变拟合曲线，推导出缓冲系数—最大应力曲线方程，并记录缓冲系数的最小值及其对应的最大应力。将这些数据添加到缓冲材料的已有材料库，进行缓冲包装设计时就可以从菜单“缓冲材料”→“已有材料”中选择材料。

4 结束语

通过静态压缩试验得到缓冲材料的应力-应变曲线，提出了3次Bezier曲线分段拟合应力—应变曲线时确定分段点和控制点的方法，进而得到了缓冲材料分段本构模型。根据3次Bezier曲线拟合的本构模型可推导出缓冲材料的缓冲系数，从而得到缓冲系数—最大应力参数方程。基于3次Bezier曲线拟合的应力-应变曲线、缓冲系数—最大应力曲线均收敛于分段点。缓冲材料本构模型、缓冲系数—最大应力方程均采用3次Bezier曲线参数方程分段表示，为计算机辅助缓冲包装设计提供了一种简洁有效的方法。基于3次Bezier曲线，提出了从缓冲材料试验开始至缓冲包装设计结束的设计流程，并探讨了开发基于3次Bezier曲线的计算机辅助缓冲包装设计软件框架。利用“已有材料”(“新材料”需处理成“已有材料”)进行缓冲设计时，只需输入W(产品重量)或S(产品表面积)、H(等效跌落高度)、G(产品脆值)即可得到缓冲衬垫的面积A和厚度T，大大提高了缓冲包装设计的效率。