约束DC优化的双束法及对偶问题*

杨 芳， 陈 恩

(重庆师范大学 数学科学学院，重庆 401331)

0 引 言

DC规划(Difference of Convex Programming)问题是非凸优化的一个重要子类，许多非凸优化问题都可以转化为DC规划问题。定义在Rn上的函数f称为DC函数，若它可以表示成两个凸函数的差。目标和约束函数都是DC函数的数学规划问题称为约束DC规划问题。

求解一个非光滑DC优化问题的方法有很多，如割平面法[1]、分支定界法[2]、DCA算法[3]等。而近年来，约束方法在求解DC优化问题上取得了很大的进展[4-11]。2017年，Joki等[4]对目标函数的DC分量函数分别建立了两个独立的分段仿射近似，结合这两个凸分段仿射近似生成一个DC函数的分段仿射模型，由此提出了一种求解无约束非光滑DC函数值极小化的近似约束方法(PBDC)，该方法收敛到一个ε-临界点。后来，该作者在此基础上又提出了一个新的停止条件使算法收敛到Clarke稳定点，即求解无约束非光滑DC优化问题的双束法(DBDC)[5]。本文先考虑L1精确罚函数构造原问题的增广目标函数，然后把无约束DC优化问题的双束法推广到带有凸约束的DC优化问题。

文章其余部分按如下方式构成：第1节介绍了本文使用的相关概念；第2节把双束法推广到带有凸不等式约束的DC优化问题；第3节证明了双束法中求解搜索方向d的对偶问题和原问题等价及相关性质；最后第4节是结束与讨论。

1 预备知识

考虑下述不等式约束DC规划问题:

(1)

其中f1(x)、f2(x)、gj(x):Rn→R,j=1,2,…,m是凸函数，函数f1、f2称为f的两个凸DC分量。

为了叙述后文，先给出以下概念：

定义1[4]设f(x):Rn→R是凸函数，则函数f在x∈Rn处的次微分定义为

∂cf(x)={ξ∈Rn:f(y)-f(x)≥ξT(y-x),∀y∈Rn}

定义2[4]函数f(x):Rn→R称为Rn上的局部Lipschitz函数，若对任意的有界集X⊂Rn,存在常数L>0，使得

称定义在Rn上的DC函数f在Rn上局部Lipschitz连续，即在任意的有界集上Lipschitz连续[6]。

定义3[5]局部Lipschitz连续函数f(x):Rn→R在x∈Rn处的广义次微分定义为

∂f(x)=conv{ξ∈Rn:∃{xi}⊂RnΩf,
s.t.:xi→x,▽f(xi)→ξ}

其中，Ωf是f的不可微集，且当f为定义在Rn上的凸函数时，∂f(x)=∂cf(x)。

假设1 对∀x∈Rn,次微分∂f1(x)、∂f2(x)是多面体集。

假设2 水平集Γ0={x∈Rn:f(x)≤f(x0)}是紧集。

2 双束法

双束法是近年来提出的解决无约束非光滑DC优化问题的一种改进的近似束方法。对于无约束非光滑DC优化问题的双束法，其主要思想是分别利用DC分量的次梯度信息构造两个束集合，因此假设在每个点x∈Rn，可以计算DC分量f1(x)、f2(x)的函数值和次梯度ξ1∈∂f1(x)，ξ2∈∂f2(x)。为了同时考虑原目标函数的凸性和凹性，利用非凸目标函数的特殊凸分解结构，对两个凸DC分量进行近似，然后将DC分量的次梯度信息收集到一个束集合中，即每个DC分量都有一个包含次梯度信息的束集合[ 5 ]。在当前迭代点xk，双束法保留的束信息为

利用凸束方法中使用的经典切平面模型思想和目标函数DC分量的凸性，就可以构造fs在当前迭代点xk处的凸分段线性近似模型[1]：

其中fs在当前迭代点xk处的线性化误差为

fs(x)≥fs(y)+▽fs(y)T(x-y),∀x∈Rn

则有

(2)

又因为线性化误差依赖于当前迭代点xk，当迭代获得一个新的迭代点xk+1时，需使用下述公式更新线性化误差：

文献[8-9]把无约束非凸优化的近似束方法推广到了约束非凸优化问题，考虑本文带有凸不等式约束的DC优化问题，对式(1)构造增广目标函数:

φ(x)=f1(x)-f2(x)+ckp(x)，x∈Rn

其中p(x)=max{gj(x),0},ck∈R+是罚参数。令φ1(x)=f1(x)+ckp(x)，则有

φ(x)=φ1(x)-f2(x)，x∈Rn

(3)

其中φ1(x)、f2(x):Rn→R是凸函数。

构造凸函数φ1(x)的分段线性近似模型：

其中p(x)在当前迭代点xk的线性化误差为

此时双束法保留的束信息为

本文考虑的DC优化问题涉及凸约束函数gj(x),利用文献[5]中的无约束非光滑DC优化问题的双束法思想，即对目标函数的DC分量函数分别构造凸分段线性近似模型,由此可以构造式(3)的增广目标函数φ(x)的凸分段线性近似模型,则有

(4)

令d:=x-xk是当前迭代点xk的搜索方向(位移)，则式(4)可等价写成

故搜索方向d是下列二次规划问题的解：

(5)

其中:

故式(5)可等价写成：

(6)

故式(6)等价于求解下述二次规划问题：

(7)

3 Lagrange对偶理论

引入式(7)的Lagrange函数：

证明式(7)的对偶问题应为

而L(d,v,α)是关于d的严格凸二次函数，先求L关于d的极小，得到

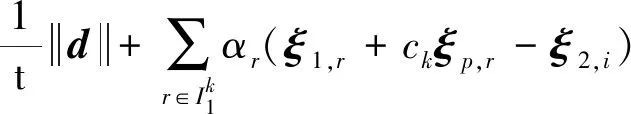
于是有

带入函数L(d,v,α)中可得

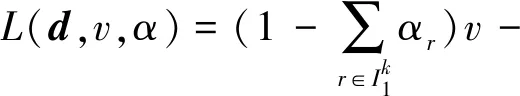
引理1 下述性质成立：

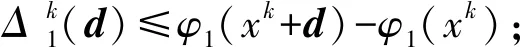
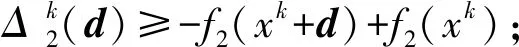
(3) 对参数t>0,有

证明(1)由f1的凸性和式(2)成立，则有

从而

(2) 证明方法同(1)。

(3) 注意，对式(5)，当d=0时，目标函数值为

定理2 对任意的近似参数t>0,有

组合得到：

(8)

最后由引理1的性质(3)可得：

(9)

化简式(9),可得定理2成立。

4 结论与讨论

双束法是近年来提出的解决无约束非光滑DC优化问题的一种非常有发展前景的近似束方法。本文首先考虑L1精确罚函数，将带有凸不等式约束的DC优化问题转化为无约束DC优化问题，然后在模型构造中，利用了非凸目标函数的显式凸DC分解结构，分别建立增广目标函数DC分量的凸分段线性近似模型，再组合这两个模型得到增广目标函数的切平面模型。此外还给出了双束法子问题搜索方向d的求解方法及对偶问题，证明了搜索方向d在范数中有界，对算法的收敛性证明起到了关键性的作用。本文考虑的约束问题是带有简单凸约束的情形，此外还可以考虑线性约束，甚至是非凸约束的情形。在此基础上，后续工作将继续研究带凸约束的DC优化问题的双束法算法。