城市中心区轨道交通站间距 优化研究
李 婷,靳文舟,朱子轩
(华南理工大学 土木与交通学院,广东 广州 510000)
0 引言
城市轨道交通作为组成城市公共交通系统的重要组成部分,是解决城市交通拥堵问题的重要切入点。站间距作为城市轨道交通网络建设的重要因素之一,其设置至关重要。合理的站间距能够缩短乘客的出行总时间,增强线路的客流吸引能力,提高线路的运营效率;同时,还能节省建设成本,最大化实现城市轨道交通的社会效益。以目前城市轨道交通建设实践来看,站间距的确定往往取决于建设者的主观经验及周边环境,容易导致站间距不合理的情况。
关于轨道交通站间距优化,国内外学者主要从运营成本、站点选址、出行时间等方面进行研究。Anthony[1]基于公交运营成本约束条件下建立平均站间距优化模型;Vladimir等[2]建立城市轨道交通枢纽站点的选址模型;Steven等[3]基于运营总成本最小为目标建立城市轨道交通站间距优化模型。王宏亮[4]利用GIS技术的空间分析对轨道交通站点进行选址,在站间距优化时重点考虑站间距不同设置方案对区域内旅客的OD出行结构所产生的影响。潘琢[5]利用双目标最短路算法和模糊多目标格序决策方法对站点分布及线路进行选择。魏金丽等[6]提出考虑客流量随站间距概率分布的合理站间距优化模型。李松等[7]从交通可达性的角度来研究铁路车站站点设置的影响因素,分析城市轨道交通站间距。
这些研究主要是针对完整的城市轨道交通网络,较少有单独针对城市中心区轨道交通站间距优化的研究。因此,在城市中心区轨道交通网络的研究基础上,以乘客总出行时间最短为目标构建站间距优化模型,以广州市中心区城市轨道交通作为案例分析,得到相应的最优站间距取值。
1 城市中心区轨道交通站间距优化模型构建
当站间距取值较大时,车辆的运行速度也就更高,乘客在车上花费的时间会更少,但较大的站距会增加人们到达站点的时间。当站间距取值较小时,车辆的运行速度低、停站时间长,增加乘客在车上的时间,但较小的站间距可以减少人们在站外的用时。乘客出行时间与站间距的关系如图1所示。
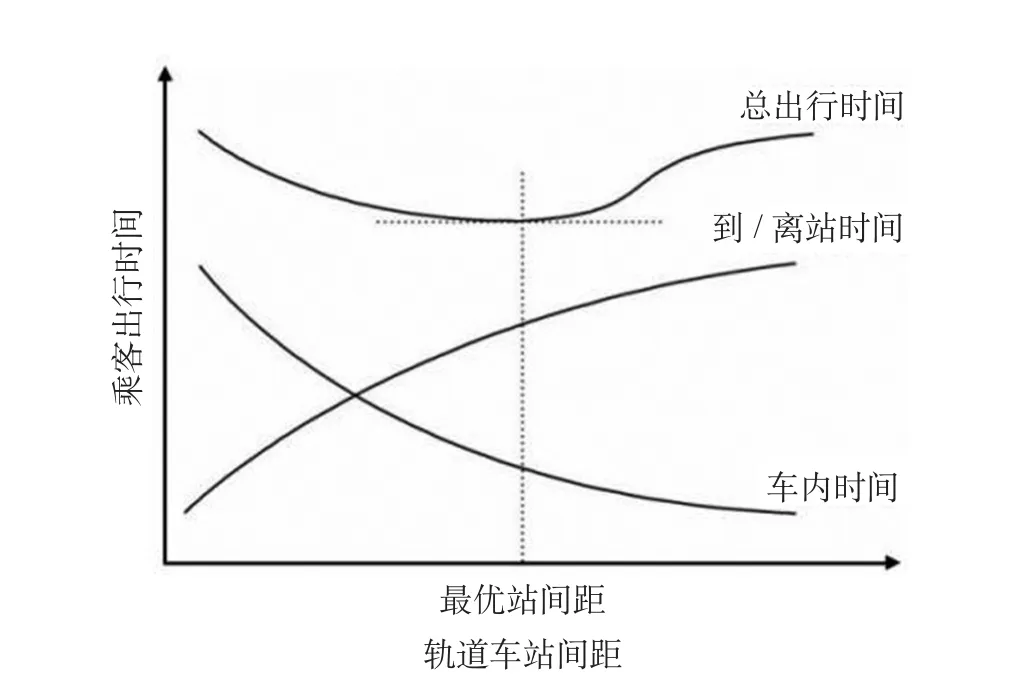
图1 乘客出行时间与站间距的关系Fig.1 Relationship between passenger travel time and station spacing
1.1 模型假设
在总出行时间曲线上存在着某个站间距值(或者区间),使其对应的乘客总出行时间值最小,这个值就是最适宜站间距。为了简化求解过程,假设如下。
(1)随着城市轨道交通的不断发展,城市轨道交通线路数量逐渐增加,增加到一定数量时,假设城市中心区的地铁线路网络将呈现一种整齐的“棋盘格式”,在此基础上,再假设每个相邻站点之间的站间距都近似相同。
(2)不考虑乘客的换乘时间,当有换乘情况时,可以看作一条线路进行处理。
(3)在城市中心区内,每个站点的吸引范围规定为以地铁站为中心、以站间距为边长的正方形区域。
(4)对于每个独立的站点而言,在其吸引范围内的客流密度是相同的,暂不考虑站点的客流量差异。
(5)在每个站点的吸引范围内,当乘客的出发地/目的地与站点的距离小于500 m时,乘客将选择步行前往;距离大于500 m时,乘客将选择坐公交车/骑自行车前往。
(6)将利用地铁从出发地到目的地的总出行时间分为3部分:乘客从出发地到达地铁站的时间T1;乘客从地铁站到达目的地的时间T2;乘客乘坐地铁的时间T3(包括等待时间、站内行走时间等)。将T1和T2合称站外时间,T3称为站内时间,假设乘客在地铁站外的出行情况是一致的,即T1和T2的构成是一致的。
1.2 站外时间模型建立
1.2.1 一般假设情况
站外时间的决定因素有:乘客的出发地/目的地离地铁站的距离和出行方式。根据模型假设,可以将站间距X取值分为3个区间范围进行计算,在每个区间范围内,利用双重积分依次计算乘客在站外出行的平均距离,进而求得站外时间。
(1)站间距X取值区间为时X≥1 km,即在每个站点的吸引范围内,乘客将选择步行或坐公交车/骑自行车前往站点。记E1为乘客步行前往地铁站的区域,E2为乘客坐公交车/骑自行车前往地铁站的区域,则当X≥1 km时乘客站外出行方式选择示意图如图2所示。

图2 当X≥1 km时乘客站外出行方式选择示意图Fig.2 Choice of travel mode outside station when X ≥1 km
在E1区域内,从出发地到最近地铁站的平均距离可表示为

在E2区域内,从出发地到最近地铁站的平均距离可以表示为
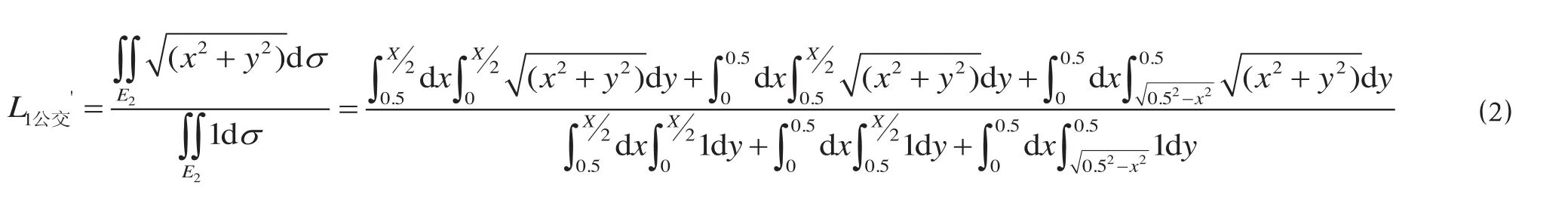
当X≥1 km时,从出发地到最近地铁站花费的时间可以表示为
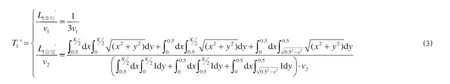
式中:T1'为从出发地到最近地铁站花费的时间,h;v1为步行的平均速度,km/h;v2为乘坐公交/骑自行车的平均速度,km/h。
(2)站间距X取值区间为时,即在每个站点的吸引范围内,乘客将选择步行或坐公交车/骑自行车前往站点。当X< 1 km时乘客站外出行方式选择示意图如图3所示。
在E1区域内,从出发地到最近地铁站的平均距离可表示为


图3 当0.5km < X < 1 km时乘客站外出行方式选择示意图Fig.3 Choice of travel mode outside station when 0.5 km < X < 1 km
在E2区域内,从出发地到最近地铁站的平均距离可以表示为

(3)当X≤ 0.5km时,即在每个站点的吸引范围内,乘客均选择步行前往站点。当X≤0.5km时乘客站外出行方式选择示意图如图4所示。
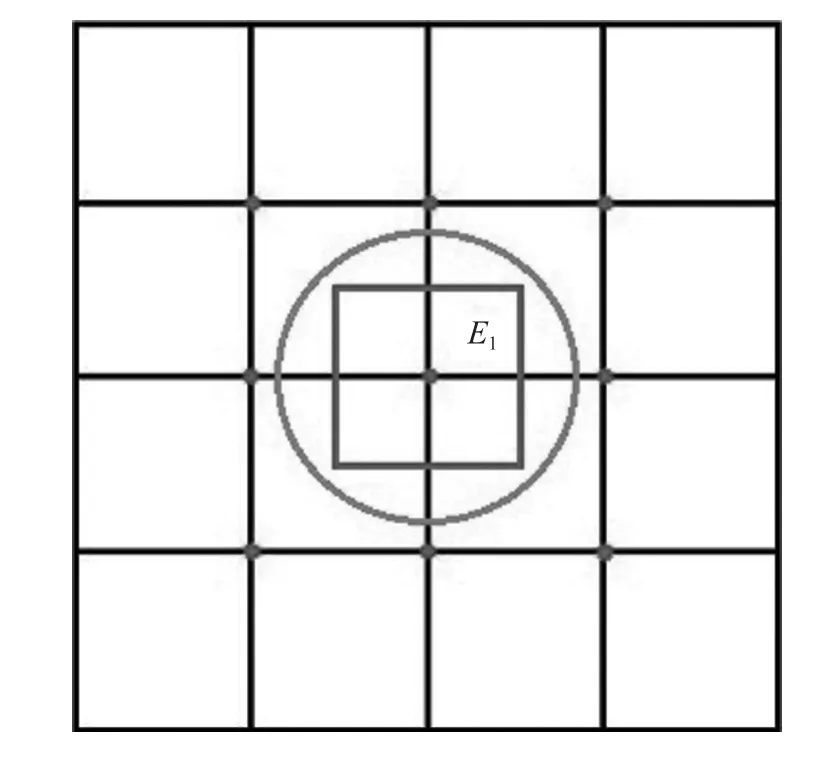
图 4 当 X ≤ 0.5km时乘客站外出行方式选择示意图Fig.4 Choice of travel mode outside station when X ≤ 0.5 km

在E1区域内,从出发地到最近地铁站的平均距离可表示为

当X≤ 0.5km时,从出发地到最近地铁站花费的时间可以表示为
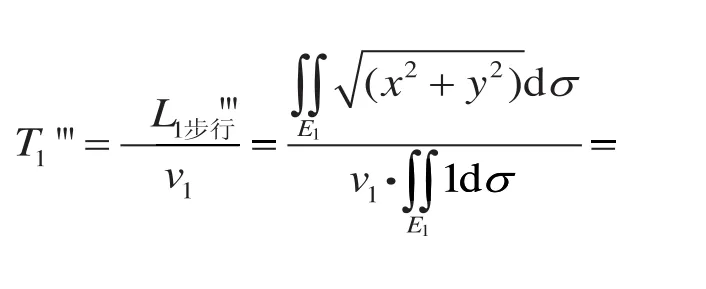
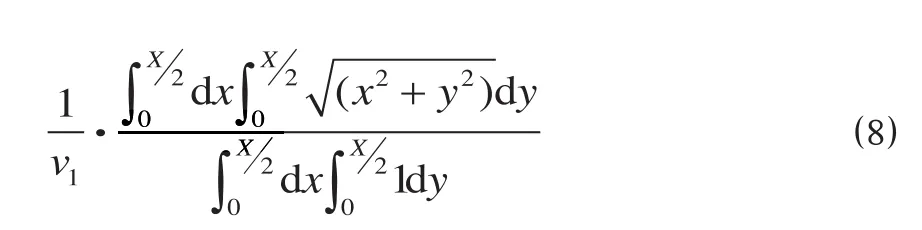
由于v1,v2的值是可以确定的,因而以上3种情况下得出的T1的模型公式是站外时间T1关于站间距X的函数关系式。同时,由于已假设乘客在地铁站外的出行情况是一致的,因而T1和T2的计算模型是一致的,则T1的模型公式也是站外时间T2关于站间距X的函数关系式。
1.2.2 特殊假设情况
虽然将乘客前往地铁站所选择的交通方式细分为步行、乘公交车或骑自行车是合乎情理的,但城市轨道交通系统在建成后要保证它的使用年限,因而在计算最适宜站间距时可以将目标放宽到未来,不妨做出超前假设。当城市发展到一定程度时,轨道交通网络建设也将更加密集与成熟,站点的覆盖率更高,在此情况下,乘客若想使用轨道交通出行,直接步行前往站点即可,不用再使用公交车或自行车等交通工具。因而可以将第5点假设替换为“在每个地铁站点的吸引范围内,乘客均选择步行前往地铁站”。
在新的假设条件下,从出发地到最近地铁站的距离和从地铁站到目的地的距离可以表示为

式中:L1为乘客从出发地到最近地铁站的距离,km;L2为乘客从地铁站到目的地的距离,km。
从出发地到最近地铁站花费的时间和从地铁站到目的地花费的时间可以表示为

式中:T1为乘客从出发地到最近地铁站花费的时间,h;T2为乘客从地铁站到目的地花费的时间,h。
1.3 站内时间模型建立
站内时间是乘客乘坐地铁花费的时间,包括乘客在车上的时间、在站内行走的时间及等待的时间。当站间距较小时,列车需要频繁停站,导致站内时间增加,适当地增大站间距可以有效节省站内时间。
假设地铁列车的运行过程为:起动时均加速至稳定运行速度,停站时从稳定运行速度匀减速至停车,则站内时间与各影响因素的关系可以表示为

式中:T3为乘坐地铁花费的时间,h;H为乘客使用地铁出行的平均距离,km;S为停站时间,h;B为列车启动及制动的总时间,h;A为列车在启动及制动过程中行驶的距离(假设加速度与减速度相同),km;V为列车运行稳定速度,km/h。
1.4 总时间模型建立
乘客的出行总时间为站外时间与站内时间之和,可以表示为

式中:T为乘客的出行总时间,h。
对公式 ⑿ 进行求导,可得

根据运动学理论,公式 ⒀ 中的变量A,B可用加速度求出,则调整后可以表示为

式中:a为列车运行加速度,m/s2。
当且仅当公式 ⒁ 成立时,乘客出行总时间T取最小值。由公式 ⒁ 可知,最适宜站间距X的大小与乘客步行速度v1、乘客出行平均距离H、列车运行稳定速度V、列车加速及减速时的加速度a及停站时间S有关。
2 实例研究
通过对广州市目前营运的13条轨道交通线路的站间距进行调研,发现广州市中心区轨道交通站间距主要集中在1.0 km到2.0 km之间,经计算,平均站间距为1.6 km。构建基于总出行时间最少的城市中心区轨道交通站间距优化模型求解如下。
2.1 最优站间距求解
根据公式 ⒁ 求解广州市中心区轨道交通的最优站间距,需要获得的数据有:乘客步行速度v1、乘客平均出行距离H、列车运行稳定速度V、停站时间S及列车加速及减速时的加速度a等。
(1)乘客平均轨道交通出行距离H。广州市轨道交通乘客的平均出行距离H需要利用轨道交通出行OD数据及广州轨道交通营运路线站间距数据来进行计算,由于研究的对象是广州中心区的最适宜站间距,因而选用基本处于中心区的1号线至6号线从2018年8月31日到2018年9月7日共8 d的全天轨道交通出行OD数据,对数据进行处理后,计算出H的值为11 km。
(2)乘客步行速度v1。根据美国道路通行能力手册[8]可知:“当行人中老年人和小孩的比例为0 ~ 20%时,平均步行速度为1.2 m/s,当老年人和小孩的比例超过20%时,平均步行速度下降到1.0 m/s。”因而可将乘客步行速度v1的取值定为1.2 m/s,即4.32 km/h。
(3)列车运行稳定速度V。对于广州市目前的轨道交通网络,不同的轨道交通路线,由于每条线使用的列车车型不尽相同,因而列车运行的参数也不尽相同,根据各方资料总结[9]加实地调研,每条线的最高运行速度及平均运行速度(均取整处理),广州市轨道交通路线的最高及平均运行速度如表1所示。
尽管目前每条轨道交通线的列车都有它的稳定运行速度,但由于这里对最适宜站间距的计算是针对未来线网发展到一种密集成熟的状态下的,因而应将模型中需要用到的稳定运行速度V取值为普遍的轨道交通列车最高运行速度80 km/h,即V= 80 km/h。
(4)停站时间S。为了看到不同情况下的最适宜站间距的差别,可以将停站时间分别取30 s,40 s,50 s和60 s来计算。

表1 广州市轨道交通路线的最高及平均运行速度km/hTab.1 Maximum and average running speed of Guangzhou rail transit line
(5)加速度a。对于加速及减速时的加速度a,可选用列车常用制动平均减速度取值1 m/s2,即a= 1 m/s2。
2.2 计算结果分析
广州市目前轨道交通的平均站间距为1.6 km。为了使H的取值更贴近现实,应对其限定一个取值区间。根据平均站间距值,可以将H的取值区间定为[9.6,12.8]。代入公式⒁进行计算,得到最适宜站间距X计算结果如表2所示。

表2 最适宜站间距X计算结果Tab.2 Calculation results of the optimal station spacing X
根据公式 ⒁ 及表2结果可以看出,在乘客平均出行距离H相同时,随着停站时间的延长,最适宜站间距的取值逐渐增大。对停站时间S以10 s为梯度逐渐增加,可以看出每增加一个梯度时,最适宜站间距的取值也跟着增加,增加的幅度呈现逐渐减小的趋势。
对于广州市这种大型城市来说,城市轨道交通承受全市公共交通出行总客流量的近一半,日均客流量目前可达600万人次以上,未来还将会继续增长。为了满足如此大的客流量,停站时间S的取值应该要较大。就目前现状而言,在体育西路站等客流量集中的换乘站,停站时间可达50 s以上;在其他客流量相对小一点的车站,停站时间也基本维持在30 s以上。因此,30 s到60 s的取值也是具有实际参考意义的。
3 结束语
城市轨道交通作为城市公共交通的重要组成部分,其建设需要满足城市的发展及乘客日益增长的出行需求,这对轨道交通网络建设的覆盖率提出了更高的要求。对于城市中心区域,合理的站间距可以在满足城市轨道交通建设要求的同时,实现最小化乘客出行时间成本,最大化城市轨道交通出行的便利性。而受到各种因素的影响,城市中心区轨道交通站间距的确定一直缺少合理的理论指导,因而建立城市中心区轨道交通站间距优化模型很有必要。基于乘客总出行时间最短的站间距优化研究利用微积分理论的计算方法,比较准确地对最优站间距的取值作出求解。另外,还应加入对站点吸引客流密度、乘客换乘时间等因素的考虑,为城市中心区轨道交通站间距的合理设置提供更好地理论依据和支持。

