全数字CDR抖动分析及改进研究

徐东明, 黄小斌

(西安邮电大学 通信与信息工程学院， 陕西 西安 710121)

随着数据业务量的不断增加，对通信系统的要求不断提高，具有高速率、大容量等优点的光纤通信成为了主流的数据传输形式。全数字时钟数据恢复(clock data recovery, CDR)电路的作用是恢复光纤通信传输系统的时钟数据并进行再定时输出。在通信系统信道中传输的数据信号一般不包含与数据信号同步的时钟信号。为了保证数据处理的同步，接收端需要使用CDR电路从数据流中提取时钟等时序信息，从含有噪声的信号中恢复出有序、有效的数字信号。

在时钟数据恢复过程中，由于接收数据的定时变化与其理想位置的时间偏差，或者是由于每个周期与其理想值的偏差导致抖动现象发生[1]。抖动导致CDR电路接收数据的定时变化。定时变化会产生错误并降低系统的效率，即使很少的时序变化也会降低系统的灵敏度[2]。为了精确地恢复出时钟信号，全数字CDR电路必须严格控制抖动。

通常采用Inverse Alexander相位检测器[3-4]和LC正交数字控制振荡器方法[5]减小全数字CDR的抖动。Inverse Alexander相位检测器方法认为抖动主要来源于相位检测器，通过调整Alexander相位检测器输出的早、晚信号来减小抖动[4]，但该方法支持的输入数据速率范围较小，核心功耗较大。LC正交数字控制振荡器方法[5]认为抖动主要来源于数字控制振荡器，其通过最小化压控振荡器比例、控制反馈环路的延迟来减小抖动，但这种方法的峰峰值抖动较高，单位能量损耗较大。

为了降低全数字CDR电路中的抖动现象，减少能量损耗，本文拟建立全数字CDR离散时间多速率模型，使用全数字CDR线性时变系统分析抖动来源，采用辅助频率锁定环的方法对数字控制振荡器进行改进，以期在降低全数字CDR电路中的抖动的同时减少电路能量损耗。

1 全数字CDR抖动来源

分析全数字CDR电路结构及原理，利用建立的离散时间多速率(discrete-time multi-rate, DTMR)模型分析全数字CDR抖动的来源。

1.1 全数字CDR电路结构及原理

全数字CDR电路的整体架构[6]如图1所示。它由多相位Bang-Bang检测器、二次采样器、数字环路滤波器和数字控制振荡器(digitally controlled oscillator, DCO)组成。

多相位Bang-Bang检测器用于确定输入数据流和恢复时钟信号之间的相位差。当时钟存在超前和滞后输入数据时,多相位Bang-Bang检测器会分别产生早、晚信号以减少或增加恢复时钟的频率。这些早、晚信号通过采样器进行二次采样降低输入数据速率，以满足数字环路滤波器(digital loop filter, DLF)工作范围的要求，由DLF滤除包含带外噪声的信号控制DCO，以减小相位误差，输出恢复的时钟信号。

图1 全数字CDR整体架构

1.2 全数字CDR离散时间多速率模型

根据全数字CDR的结构，建立DTMR模型分析全数字CDR抖动。全数字CDR输入信号的离散时间多速率模型原理如图2所示。

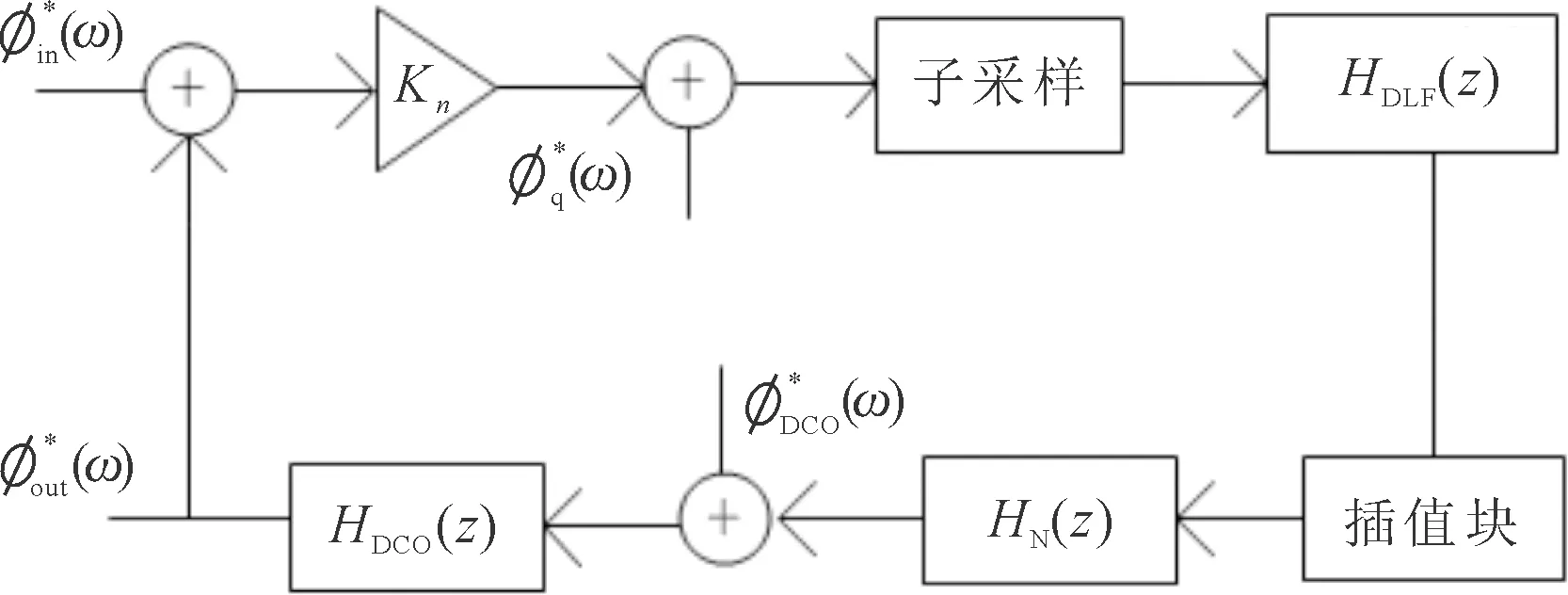
图2 离散时间多速率模型原理

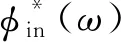
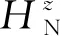
(1)

其中，Tclk表示时钟周期，KDCO表示DCO的增益。

在s域的零阶保持器传递函数[8]可以表示为

(2)

其中Tdig表示数字时钟周期。

1.3 全数字CDR抖动的来源

建立了全数字CDR的离散时间多速率模型后，下面将在全数字CDR线性时变系统的频域分析抖动来源。

离散时间多速率系统输出信号的相位频谱[9]可以表示为

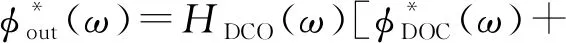
(3)

其中，HDCO(ω)表示DCO在ω域的传递函数，HN(ω)表示零阶保持器在ω域的传递函数，HDLF(Nω)表示在采样因子为N条件下DLF在ω域的传递函数，F(Nω)表示在采样因子为N条件下对样本序列输出信号频谱F(ω)进行的二次采样。

F(Nω)和F(ω)的频谱函数可以分别表示为

(4)

DLF在ω域的传递函数[6]可表示为

(5)

其中T(ω)表示样本序列在ω域的周期。

将式(4)代入式(3)中可得

(6)

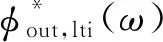
(7)

将式(6)代入式(7)的求和项中，由于舍去输出信号相位频谱的高次谐波分量，所以

(8)

由式(8)可知，全数字CDR环路中各个不相关噪声源输出相位的功率谱密度函数[10]的表达式为

(9)

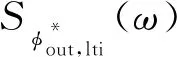
(10)

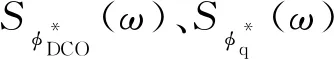
由于时域的抖动和频域的输出相位功率谱密度函数存在正相关关系[12]，所以式(10)表明了全数字CDR产生的抖动主要来自于数字控制振荡器，可以通过改进DCO来降低抖动。

2 数字控制振荡器的改进

2.1 辅助频率锁定环的采用

为了扩大采样频率的锁定范围，在复位全数字CDR时使能，保证正确的采样频率操作，降低锁定期间的抖动性能，采用辅助频率锁定环[13](frequency locked loop，FLL)锁定采样频率。

2.2 DCO的设计

为了兼顾4相位和8相位时钟，对齐数字边沿与时钟相位[14]，采用四级差分振荡器设计DCO。四级差分振荡器每级都有一个8位微控制电容器组，其中4位最高有效位采用二进制编码，4位最低有效位采用温度计编码，以减少锁定期间的切换活动。四级差分振荡器结构如图3所示。

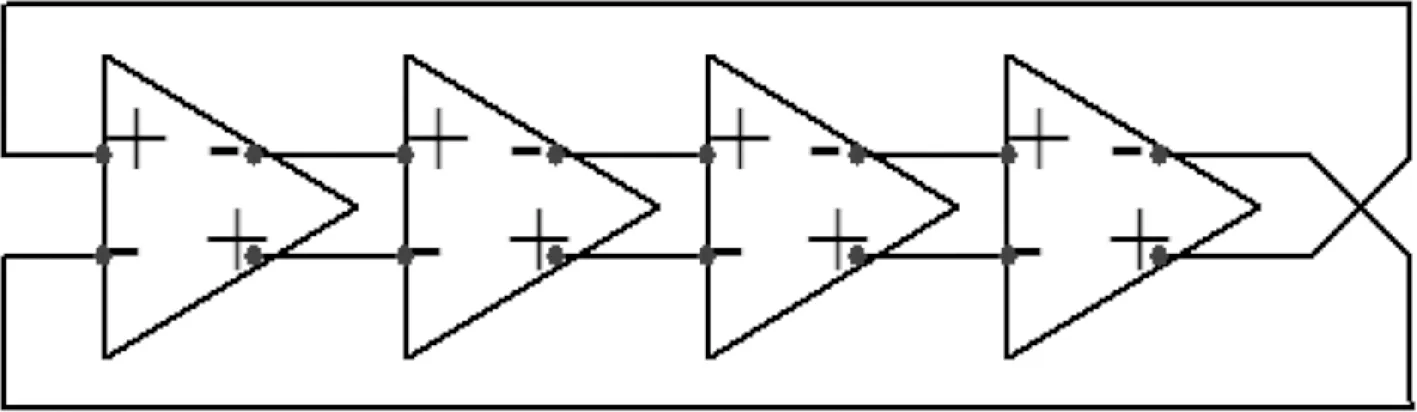
图3 四级差分振荡器结构

在设计过程中，采用型号为YSO8918MR的可编程DCO，使用硬件描述语言Verilog编程完成DCO的电路设计，再将其程序烧录至FPGA上进行多次测试，发现当环路作为多相位Bang-Bang检测器运行时，不会影响稳态抖动性能。

图4 确定DCO输出序列与参考时钟相位误差

2.3 DCO的校准

在全数字CDR正常工作之前，需要对DCO进行校准。首先应该将DCO频率调整到输入数据速率的四分之一频率处，上下浮动约±30 MHz[15]。例如当输入数据速率为25 Gb/s时，调整到6.25 GHz。为此，在校准周期中，通过一个基于外部参考时钟和计数器的自动频率控制环路完成DCO的粗调。频率控制环路对数字时钟和外部参考时钟的时钟周期数进行计数，将计数与串行接口的寄存器值进行比较，逐渐调整，直到DCO频率位于所需频率上下浮动±30 MHz的范围内。

3 仿真结果及分析

在3.3V电压下，利用具有正弦抖动的26 Gb/s数据序列作为输入数据，以采样因子N=16进行二次采样，进行全数字CDR抖动值测量，并应用MATLAB仿真120次。文献[3,5]以及本文设计的抖动幅度随抖动频率的变化趋势如图5所示。

可以看出，随着抖动频率的增加，文献[3]、[5]及本文方法的抖动幅度都呈现上升的趋势。随着输入数据速率的不断提高，数字控制振荡器的抖动不断加大，使得全数字CDR的抖动幅度增加[16]。本文设计采用了辅助频率锁定环扩大了采样频率的锁定范围，FLL在复位全数字CDR时使能，并保证正确的频率操作，降低了锁定期间的抖动，导致本文设计的CDR产生的抖动幅度低于其他两种CDR。

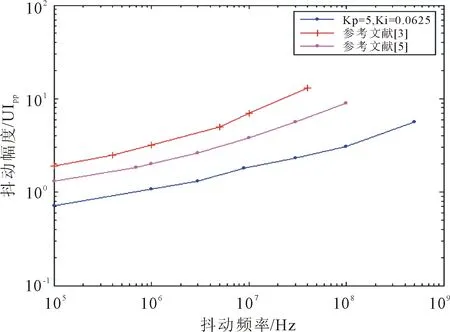
图5 抖动幅度曲线

全数字CDR的眼图仿真结果如图6所示。可以看出，由于采用了辅助频率锁定环扩大了采样频率的锁定范围，导致DCO可以进行更准确地锁定频率，即在眼图张开最大的时刻进行数据的采样，因此，降低了系统的抖动。

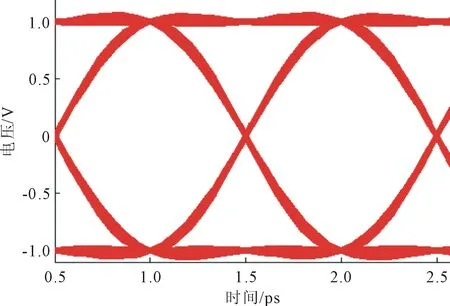
图6 全数字CDR的眼图仿真结果

文献[3]、[5]及本文方法的数字CDR性能仿真结果如表1所示。可以看出，本文方法支持的输入数据速率为13.0 Gb/s～26.0 Gb/s，峰峰抖动值为1.19 ps，单位能量损耗为2.3 pJ/bit，满足抖动掩膜要求。与文献[3]和[5]相比，本文方法支持的输入数据速率较宽、峰峰抖动值较小、单位能量损耗较低。

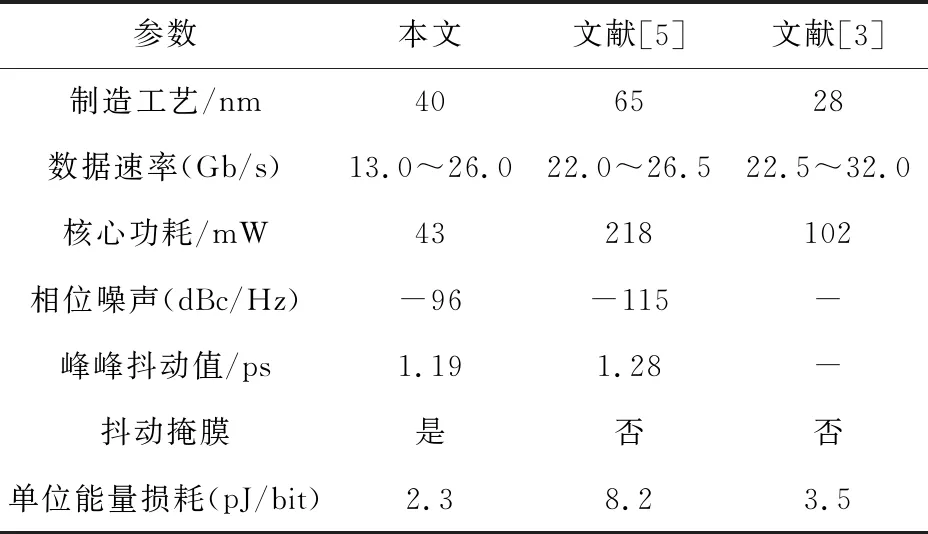
表1 不同方法的数字CDR性能仿真结果

4 结语

通过全数字CDR线性时变系统的频域对抖动分析，得出抖动主要来源于DCO。进而采用辅助频率锁定环改进DCO的抖动性能，减小了DCO的抖动。与Inverse Alexander相位检测器方法和LC正交数字控制振荡器方法相比，不仅提高了输入数据速率范围，而且降低了系统的峰峰抖动值、单位能量损耗。