基于非局部信息的截集式PCM图像分割算法
曹雪红, 高梦飞, 范九伦, 雒 僖, 于海燕
(1.西安邮电大学 自动化学院, 陕西 西安 710121; 2.西安邮电大学 通信与信息工程学院, 陕西 西安 710121)
图像分割[1]是把所选中的图像根据纹理、灰度、形状、颜色等特定准则划分成若干个具有相同性质的类别的过程,是从图像处理到图像分析的关键步骤。图像分割的常用方法有阈值分割[2]、区域分割[3]、边缘分割[4]和聚类分割[5]等,其中模糊C-均值聚类 (fuzzy C-mean clustering,FCM) 算法[6]是最经典的模糊聚类算法之一。FCM算法要求样本点到各个聚类中心的隶属度之和为1,受此约束条件的影响,FCM算法对噪声点比较敏感。为克服FCM对噪声敏感的缺陷,Krishnapuram等人提出了可能性C-均值聚类(possibilistic C-means, PCM)算法[7],该算法放弃了FCM算法的隶属度和为1 的约束条件,构建了一个新的目标函数。PCM算法使得噪声数据点得到的隶属度值比较小,对聚类分割结果来说,噪声对其产生的影响可以忽略,但是, PCM算法对初始聚类中心比较敏感,容易产生一致性聚类结果。
针对PCM一致性聚类的缺点,学者们提出了一些改进的算法。Pal等人[8]在FCM和PCM算法的基础上提出了可能性模糊C-均值聚类 (possibilistic fuzzy C-means,PFCM) 算法,克服了一致性聚类的缺点。YU等人[9]提出了截集式可能性C均值聚类(cutset-type possibilistic C-means,C-PCM) 算法,该算法将截集引入到PCM算法中,利用截集的概念产生聚类核,然后对聚类核内像素点的隶属度进行修改,最后把类间关系和可能性聚类结合起来,从而避免了PCM一致性聚类的结果,但是,C-PCM算法未考虑到邻域像素点的信息,对被高斯噪声污染的图像不能获得较好的分割结果。为此,基于邻域空间信息的FCM(FCM with spatial constraints, FCM_S)算法[10]是在FCM算法中增加了图像的局部空间信息,分别对FCM算法的目标函数加入均值空间信息和中值空间信息[11],从而提高了算法的运算效果。与局部空间信息相比,非局部空间信息从整幅图出发,充分利用图像中的冗余信息,从而很好地保证了图像的细节部分。基于非局部空间信息的FCM(FCM with non-local spatial information, FCM_NLS)算法[12]将非局部空间信息引入到FCM算法中,提高了算法针对噪声的鲁棒性。
为了进一步增强算法的抗噪性能,更好地保留图像中的细节信息,本文算法将非局部空间信息和C-PCM相结合,提出了基于非局部空间信息的截集式可能性C-均值聚类(cutset-type FCM_NLS,C-PCM_NLS)算法。并且分别对4种不同类型的实验图像进行分割结果测试,以验证算法的有效性。
1 相关图像分割算法及理论
1.1 模糊C-均值聚类算法
给定一个图像样本集X={x1,x2,…,xn},模糊C-均值聚类算法通过对目标函数进行不断的迭代优化实现样本的划分,从而将n个样本分成c个聚类中心。FCM的目标函数定义为
(1)
其中,uki表示第i个样本属于第k类的隶属度,并构成隶属度矩阵U=[uki]c×n;m为模糊因子,表示算法对聚类结果的模糊程度,通常m取值为2;vk表示第k个聚类中心,组成聚类中心的集合V={v1,v2,…,vc};d(xi,xk)=‖xi-vk‖表示第i个样本到第k个聚类中心的欧式距离。采用拉格朗日乘子法对目标函数求最小值,可得到隶属度和聚类中心的更新迭代公式分别为
(2)
(3)
FCM算法要求样本点到聚类中心的隶属度之和为1,受此约束条件的影响,FCM算法抗噪性能较差。
1.2 可能性C-均值聚类算法
PCM算法[7]是对FCM算法改进算法,主要通过放弃隶属度的约束条件,改进了噪声敏感的问题。PCM算法的目标函数为
(4)
约束条件为
(5)
其中,tki表示第i个样本到第k个类的典型性值,且构成可能性划分矩阵T=[tki〗],ηk为惩罚因子,其计算公式为
(6)
式中K为参数,通常K=1。通过迭代优化得到的典型性值和聚类中心的计算公式分别为
(7)
(8)
PCM放弃了FCM中隶属度的约束条件,由式(7)可知,如果样本i属于第k个类,即其典型性值只与该类有关,与其他聚类没有关系,这样容易导致一致性聚类的结果。
1.3 截集式可能性C-均值聚类算法
PCM算法放弃了对隶属度的约束条件,使得它对噪声点或者奇异点有较强的鲁棒性,但缺点是会导致一致性聚类的结果。为解决PCM算法存在的一致性聚类的问题,截集式可能性C-均值聚类算法(C-PCM)将截集[11]的概念引入到可能性聚类中,利用β截集为每一类产生一个聚类核,并且对聚类核内每一个样本点的典型性值进行修改,将类与类之间的关系引入到可能性聚类中,克服了PCM一致性聚类的缺点。C-PCM算法的目标函数如下
(9)
约束条件为
(10)
其中η是所给定的常数,在该算法中取固定的值。典型性值的更新公式以及聚类中心的更新公式为公式(7)和公式(8)。
C-PCM算法在每一次迭代的过程中对样本的典型性值进行修改。具体的典型性值修改过程是先用公式(7)求出样本的典型性值,然后获取样本点xi到所有类的典型性值的最大值,即tqi=max{tki,1≤k≤c}获胜典型性值。若tqi满足
(11)
式中β为截集门限,且0≤β≤1,则认为样本点xi属于第q类,而不属于其他类,然后,将样本点到其他类的典型性值修改为0,并且tqi保持不变。其具体修改方式为如果tqi>β,则
(12)
如果tki≤β,则
tki-tki,k=1,…,c。
(13)
显然,当β=1时,C-PCM算法转化成PCM算法。
1.4 非局部空间信息
与局部均值算法相比,利用非局部均值算法生成的空间信息更能给予像素点更大的权值,可以更好的反映出像素间的相似性。
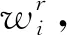
(14)

(15)
式中,h是控制权值wip衰减的因子,h通常取值为噪声方差的0.3倍;x(Ni)是以像素i为中心、大小为s×s的相似窗Nj上的灰度向量,zi是一个归一化常数,其定义为
(16)
2 C-PCM_NLS算法
由于C-PCM算法和FCM算法均未考虑图像的空间邻域信息,直接对图像的像素的灰度值进行处理,所以,在处理受高斯噪声污染的图像时,上述两种算法均不能获得较好的分割效果。为此,本文在C-PCM算法的目标函数中加入了非局部空间约束项,给出一种基于非局部空间信息的截集式可能性C均值图像分割算法。
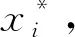
(17)
采用拉格朗日乘子法对目标函数求最小值。对利用目标函数对tki求偏导数,可得
(18)
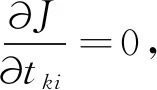
(19)
同理,求目标函数关于vk的偏导数并令其为0,可以得到聚类中心的更新公式
(20)
C-PCM_NLS算法应用于图像分割的具体步骤如下。
步骤1给定聚类数目c,模糊因子m,惩罚因子η。设置最大循环次数rmax和算法停止的阈值ε。

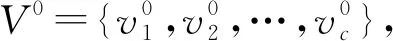
步骤4利用公式(19)更新典型性值。
步骤5修改典型性值。令tqi=max{tki,1≤k≤c},如果tqi>β,则根据公式(12)修改典型性值,否则,根据公式(13)修改典型性值。
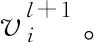
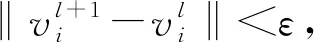
3 实验结果及分析
为测试C-PCM_NLS算法的性能,分别选取人工合成图像、#15088图像、脑部医学图像以及刑侦图像等4幅不同种类的测试图像进行图像分割,并与FCM算法[6]、C-PCM算法[9]、FCM_S1算法[11]、FLICM算法[13]、FCM_NLS算法[12]等5种算法的实验结果进行对比。
实验采用MATLAB R2014a软件系统,算法参数设置分别为m=2,最大迭代次数rmax=100,停止的阈值为ε=0.000 01。FCM_S1、FLICM算法局部邻域窗口为3×3,FCM_NLS算法以及本文算法的搜索半径为10,邻域窗口半径为3。
在图1中,(a)为选取的原始图像,(b)为加入了均值为0且方差为0.06的高斯噪声的图像,并将本文算法与其他5种算法进行图像分割实验,结果图1(c)~(h),分别表示FCM算法、C-PCM算法、FCM_S1算法、FLICM算法、FCM_NLS算法以及本文C-PCM_NLS算法的分割结果。

图1 人工图像分割效果图
可以看出,FCM和C-PCM算法对含噪图像的分割效果相比不理想,分割后的图像中包含的噪声点较多和含噪图像之间差别很小,这是因为FCM、C-PCM算法都是直接对图像中的像素点进行聚类,导致算法对噪声比较敏感。而FCM_S1算法先对图像进行均值滤波,并结合了滤波后的图像像素,分割效果所含的噪声点相对较小。相比而言,FLICM算法将图像的邻域灰度信息和局部空间信息相结合,分割后的图像含有少量的噪声点。FCM_NLS算法和本文算法都基本上消除了图像中的噪声点,在视觉上没有太大的区别,都能得到较好的分割结果。
为进一步评价本文算法的分割性能,采用通常的峰值信噪比(peak signal to noise ratio, PSNR)聚类性能进行定量评价,PSNR计算公式为
(22)
式中MSE表示原图像与处理图像之间的均方误差(mean square error,MSE),其计算公式为
其中,I(i,j)表示利用聚类算法对噪声图像去噪后得到的分割结果,K(i,j)表示不含噪声的图像的分割结果。MN表示图像所含的像素点。通常情况下,PSNR越大,表示图像分割效果越好,算法的抗噪性能越好。
为研究本文分割算法在不同高斯噪声的聚类性能,实验中采用对人工合成图像分别添加方差为0.06和0.08的高斯噪声后,进行图像分割,将上述6种算法分割后的准确率以及 计算结果如表1所示。
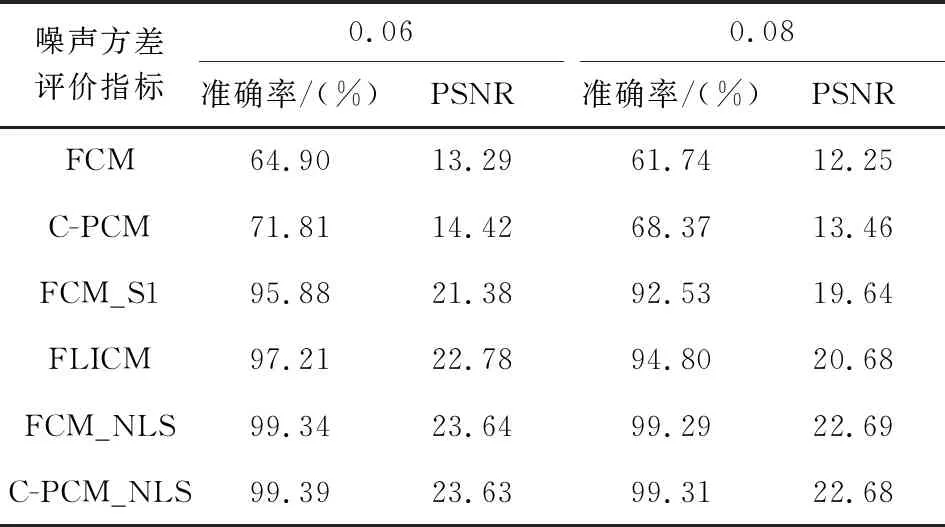
表1 不同算法对高噪人工图像的聚类性能
从结果可以看出,相比其他4种算法,C-PCM_NLS算法和FCM_NLS算法对含有同一高斯噪声的人工图像分割,能够得到更高的准确率和PSNR值,在噪声方差改变的情况下,准确率和PSNR值较其他4种算法变化幅度不大,说明该算法与FCM_NLS算法的抗噪声性能较好。
为了进一步说明本文算法的性能,分别选取了自然图像,医学图像以及刑侦图像进行了对比实验,自然图像图2(a)为原始图像,图2(b)加入了均值为0,方差为0.06的高斯噪声,图2(c)~(g)分别是使用上述5种算法与C-PCM_NLS算法的分割结果。

图2 #15088图像分割效果图
从6种算法的分割效果可以看出,FCM基本没有抗噪性能,C-PCM有较弱的抗噪性能,FCM_S1算法在FCM算法中加入了空间邻域信息,从而分割效果相比于前两种算法有所改善,但是仍存在着部分噪声点,相比而言,FLICM算法分割后的图像中含有少量的噪声点。FCM_NLS算法和C-PCM_NLS算法更好的抑制了噪声,两者的分割效果在视觉上没有较大的区别。
图3中对加入了均值为0,方差为0.08高斯噪声的脑部医学图像进行了分割对比实验,图3(c)~(h)分别对应6种算法的分割效果图。可以看出,其中FCM算法和C-PCM算法受噪声影响严重,分割后仍存在大量的噪声点,其原因是FCM算法和C-PCM算法把噪声看作正常像素点,并未考虑图像中像素的邻域信息,导致这两种算法无法区分噪声数据。FCM_S1算法和FLICM算法都结合了图像的局部信息,更多的利用了图像中像素的邻域空间信息,但是仍存在少量的噪声点。FCM_NLS算法和C-PCM_NLS算法结合了非局部空间信息,可以更好地去除像素点周围的噪声点,含有的噪声点最少。
图4中选取5种算法与本文C-PCM_NLS算法对刑侦图像进行分割效果对比,效果如图4所示。
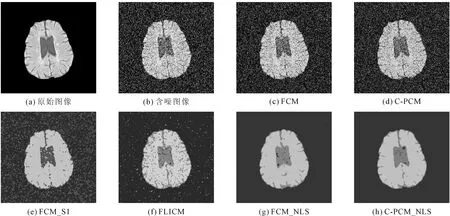
图3 脑部分割效果图
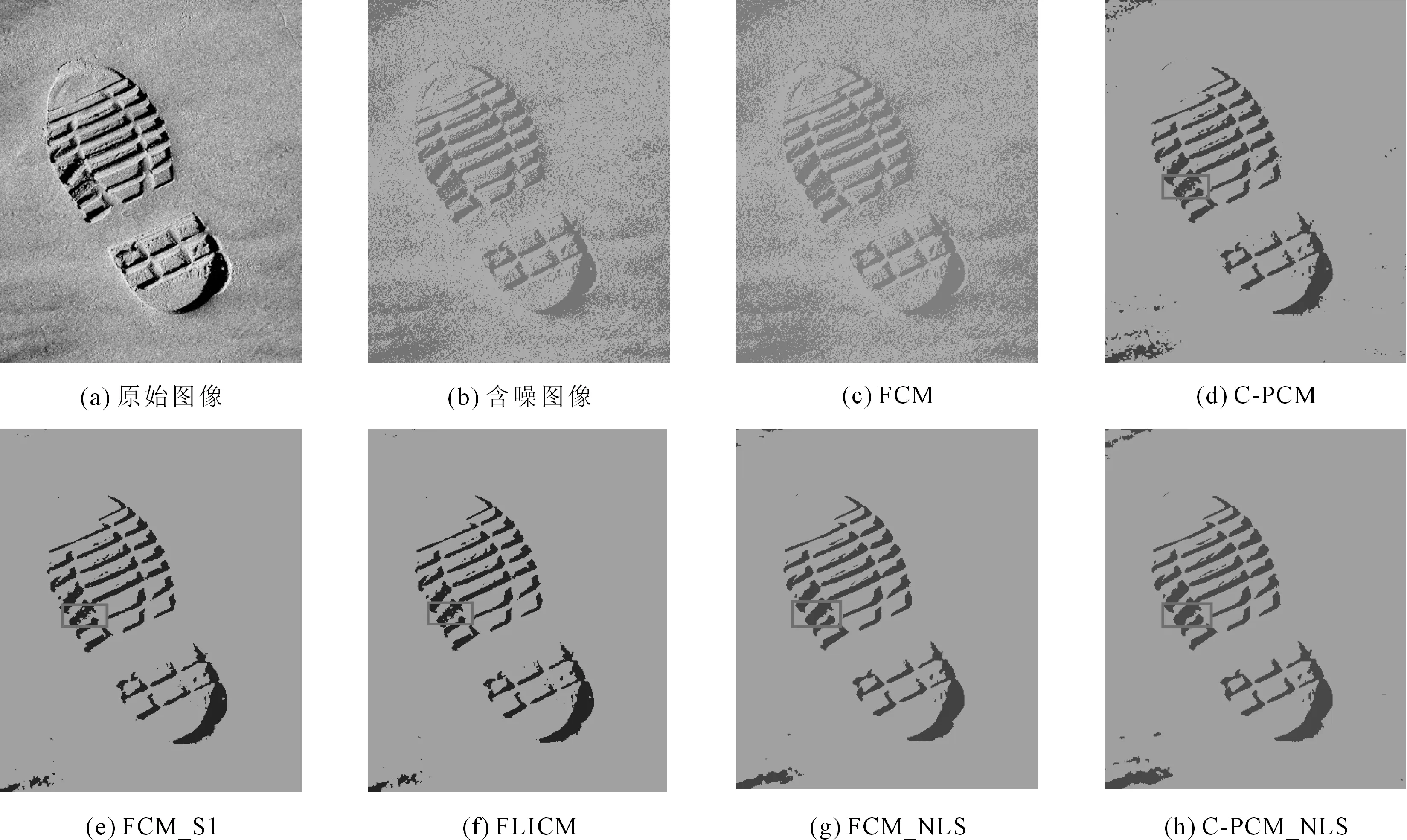
图4 刑侦图像分割效果图
从图中显示的分割效果可以看出,FCM和C-PCM由于没有考虑图像像素的邻域信息,分割效果相对来说比较差,目标图像和其背景图像不能明显划分,得到的脚印图较为模糊,并且局部细节没有突出,这两种算法在实际侦查中效果不佳。而FCM_S1算法和FLICM算法由于将空间局部信息考虑其中,从而保留了图像的局部细节,能够获得较为清晰的脚印图,其中,相比较于FCM_S1算法、FCM_S2算法而言,FCM_NLS算法和C-PCM_NLS算法可以得到较为清晰的脚印细节部分,如图中方块标注所示。
4 结束与讨论
针对PCM没有考虑图像像素的空间信息,且对高斯噪声敏感的缺点,提出了一种基于非局部空间信息的截集式可能性聚类图像分割算法。该算法利用像素间的非局部空间邻域信息,通过对含有高斯噪声图像进行仿真实验,结果表明相比于FCM算法、C-PCM算法、FCM_S1算法、FLICM算法,本文C-PCM_NLS算法与FCM_NLS算法效果相同,既可以进一步改善噪声图像的分割效果又能保留图像更多的细节信息。
不同的截集门限对应着不同大小的聚类核,合适的聚类核会降低噪声对分割效果的影响,因此,优化和修改截集门限,降低噪声对分割效果的影响,从而减少算法的迭代次数,是有待于进一步研究的问题。

