站钟约束的实时动态精密单点定位

芈小龙, 向 敏

(海军装备部, 北京 100481)

随着全球卫星导航系统(global navigation satellite system，GNSS)技术发展及应用，国际GNSS服务(international GNSS service, IGS)已逐步发布精密轨道和钟差[1]，使近年来精密单点定位(precise point positioning, PPP)技术得以快速发展[2]。目前，PPP技术已经广泛应用于高精度定位、导航与授时[3-4](positioning, navigation and timing, PNT)。李星星等人[5]研究了GNSS PPP定位结果，使PPP水平方向可以达到毫米量级，高程方向可以达到厘米量级；同时，相对于单系统，多系统能够明显缩短收敛时间。葛玉龙等人[6]基于国际GNSS监测评估系统(international GNSS monitoring & assessment system)发布的精密产品，研究了全球定位系统(global positioning system，GPS)和北斗卫星导航系统(BeiDou navigation satellite system，BDS)PPP时间传递，结果显示基于BDS区域系统进行PPP时间传递的精度可以达到0.8 ns。然而，上述研究主要基于事后数据处理，无法满足实时用户。

从2007年开始，IGS研究实时PPP(real-time pilot project, RTPP)，并于2013年正式发布实时精密产品[7-8]，这为实时PPP应用带来一系列的机遇与挑战。卢翠鲜等人[9]基于IGS实时流和多系统产品对实时对流层进行了研究，结果表明，相对于实时GPS单系统，实时多系统PPP可以提高对流层精度约为22.2%。刘腾等人[10]建立和分析了基于原始观测的实时PPP的电离层应用，其研究结果表明实时PPP能够求解一个较好的斜电离层参数。王亮等人[8]分析了实时多系统精密产品，并研究了模拟实时多系统PPP定位，模拟实时动态PPP定位在水平精度约为3～4 cm，高程方向约为5～7 cm。

众所周知，受卫星定位受几何条件的限制，GNSS精密定位获得的测站高程精度明显比平面精度差。造成GNSS定位高程精度相对较差的主要因素是接收机只能捕获来自地平线以上的可视卫星，这种几何上非对称性的观测条件使得测站高程参数、天顶对流层以及接收机钟差等参数之间存在明显的数学相关性。此外，上述研究没有顾及相关参数的相关性。葛玉龙等人[4,11]对钟进行建模，并将其应用事后和实时PPP时间传递，研究表明钟建模能够明显提高时间传递的精度。而对站钟模型约束的实时PPP动态定位研究非常少。基于此背景，本文在法国国家太空研究中心(centre national d’etudes spatiales，CNES)发布的实时精密产品CLK93以及外接高性能原子钟的观测数据，对测站钟差建立模历元间约束模型，并进行实时PPP动态定位，以期达到较好的效果。

1 数学模型

1.1 PPP模型

为了消除一阶电离层影响，PPP采用无电离层双频组合观测值，其数学模型可以表示[12-13]为

(1)

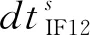
(2)

式中dr,j为接收机端码延迟，dtr为接收机钟差，α和β为相应的系数，可分别表示为

1.2 钟差历元间约束模型

在PPP数据处理过程，钟差参数通常被当作白噪声估计，因而难以顾及钟差历元间的相关性。从自相关函数可以明显的看出，历元间钟差具有强相关[4]，因此，可以通过自相关函数来获取其历元间相关性。

本文采用随机游走模型即历元间约束模型[4,11]来估计钟差参数，其中过程噪声Qw可以表示为

Qw=[δAllan(τ)τc]2。

(3)

式中δAllan(τ)为采样间隔τ所对应的Allan偏差。值得注意的是δAllan(τ)由IGS提供的最终精密产品中的接收机钟差参数计算而获取。考虑到IGS提供的接收机钟差采样间隔为5 min，而本文数据处理的采样间隔为30 s，因此，需要计算出30 s所对应的Allan方差，其计算公式为

(4)

式中q0、q1、q2和q3分别为调相白噪声、调频白噪声、调频随机游走噪声和调频随机奔跑噪声。如IGS未提供接收机钟差的站点，可基于IGS提供的最终精密产品进行GPS PPP解算进而获得接收机钟差参数。值得注意，由于采用最小二乘法来估计4个系数，如果接收机发生大的钟跳，则当前历元的钟差参数需要按白噪声模型估计。

2 实验数据及处理策略

试验选取5个外接高性能原子钟的GNSS跟踪站，图1给出了站点分布图。观测时间为年积日(day of year, DOY)182-202, 2018, 观测值的采样间隔为30 s。实时精密产品由CNES实时发布的CLK93。以一天的观测数据为一个弧段进行解算，共105组实验。表1列出了详细的PPP处理策略。实验首先估计接收机钟差过程噪声参数，其次将其应用模拟实时PPP动态定位。值得注意的是由于本文采用的模型是根据站钟的特性来确定，因而所计算的过程噪声不要每次数据处理都进行估计，且可以长期使用。

图1 站点分布图

误差项说明一阶电离层消电离层组合参数估计Kalman滤波对流层延迟ZHD: Saastamoinen模型改正;ZWD:投影函数采用GMF模型卫星天线 PCO 和 PCVIGS ANTEX 观测值消电离层组合的伪距和载波观测值采样间隔30s信号选择GPS: L1/L2定权高度角定权截止高度角10°相对论效应模型修正Sagnac效应模型修正潮汐IERS2010[14]相位缠绕模型修正[15]接收机钟差(1)白噪声模型 (2)历元间约束模型站坐标静态估计模糊度作为常数进行估计;浮点解

3 算例结果分析

本文主要分为两种处理方案，如表2。方案1是基于CNES提供实时产品CLK93进行实时动态GPS PPP定位，其中钟差参数采用白噪声模型来进行估计。方案2是基于CNES提供实时产品CLK93进行实时动态GPS PPP定位，其中钟差参数采用历元间约束模型。

表2 数据处理方案

图2(a)、(b)、(c)和(d)分别给出了NIST、 IENG、OPMT和WAB2站在DOY 201 GPS PPP动态定位误差在东(East, E)、北(North, N)、高(Up, U)等3个方向上的时间序列，图中横坐标为协调世界时(coordinated universal time，UTC)，为国际标准时间，时间历元以小时(hour，h)为单位，纵坐标为E、N、U等3个方向上的动态定位误差，单位为m。由图2可以得到以下4点结论。

(1)目前实时动态PPP定位收敛后能够达到厘米量级。

(2)方案1计算得到高程方向的定位误差明显比水平方向差，可以从定位误差的噪声以及波动情况看出。其主要原因是由于接收机只能捕获来自地平线以上的可视卫星，这种几何上非对称性的观测条件使得测站高程参数、天顶对流层以及接收机钟差等参数之间存在明显的数学相关性。

(3)方案2的定位结果明显优于方案1，尤其在高程方向，而水平方向相差大大，其主要原因是由于方案2对接收机钟差进行建模，考虑了接收机钟差历元之间的相关性，对接收机钟差历元间进行约束，降低了接收机钟差参数与高程方向的相关性，进而提高高程方向的定位精度。另一方面，从图中也可以看出，方案2的高程方向定位误差的噪声明显小于方案1，其进一步说明了本文方法的优越性。

(4)图中还可以看出，方案2除了高程方向表现出较好的结果，结果并没有明显的系统差和较大的波动，进一步说明了本文方法的可靠性。

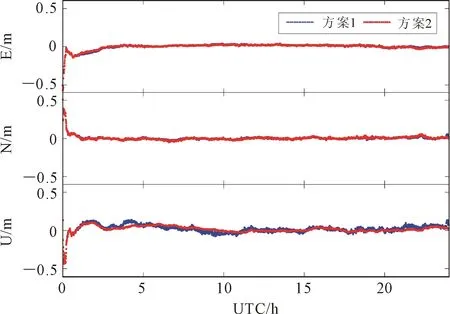
(a) NIST站计算结果

(b) IENG站计算结果

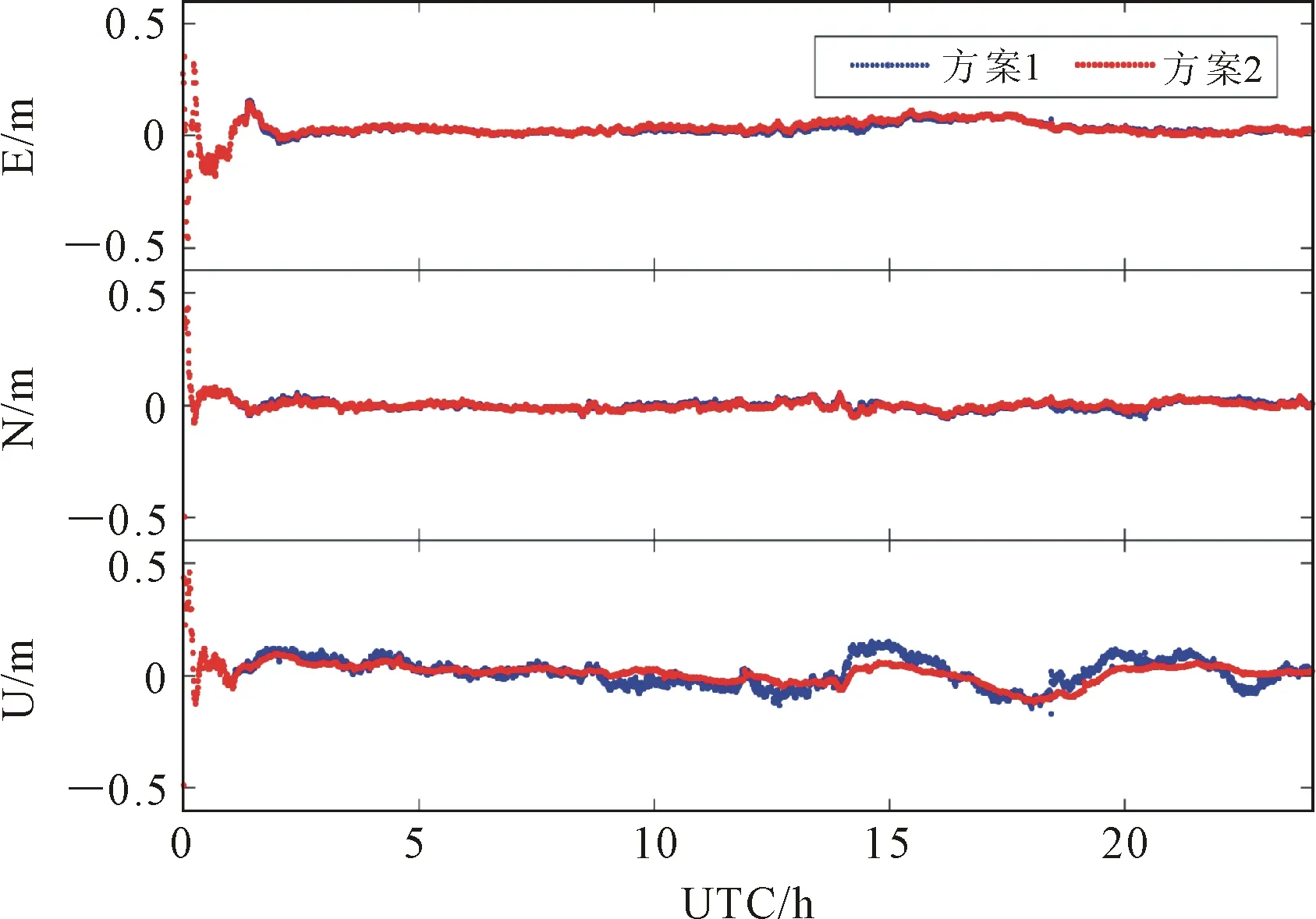
(c) OPMT站计算结果

(d) WAB2站计算结果

为进一步对两种方案的定位结果进行量化，计算了所有实验结果的均方根误差(root mean squares, RMS)，其统计结果如图3所示。同时，表3中给出了所有结果的RMS的均值。结合图3和表3，可以得到以下3点结论。

(1)N方向的定位精度主要集中于2～3 cm范围内，明显高于E方向和U方向，E方向的定位精度主要集中于3～5 cm范围内。

(2)相对于方案1，方案2在E和N方向上定位精度有一定的提高，但不是非常明显，而在高程方向提高非常明显，从图3中可以看出，方案1的定位精度主要集中在4～7 cm范围内，而方案2的定位精度主要集中于3～6 cm范围内。

(3)从表3中可以看出，目前实时GPS PPP动态定位在水平面的精度约为2～3 cm，高程方向的精度约为5 cm。站钟约束的实时动态GPS PPP定位在E、N 和U方向上的精度分别3.93、 2.01 和3.75 cm。相对传统的实时动态GPS PPP定位，站钟约束的实时动态PPP在E、N 和U方向上分别提高1.26%、2.43%和23.16 %。

图3 两种方案计算定位误差的RMS

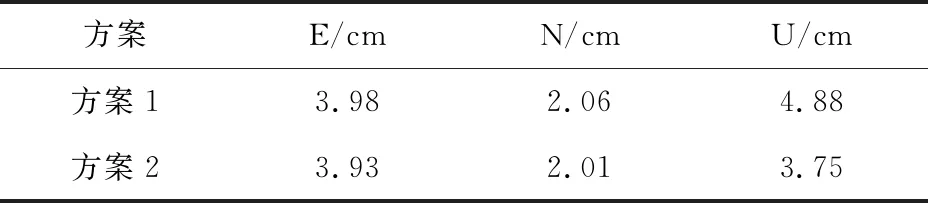
方案E/cmN/cmU/cm方案13.98 2.06 4.88 方案23.93 2.01 3.75

4 结束语

针对当前IGS发布的实时产品以及许多GNSS跟踪站装备了高性能的原子钟情况，首先根据站钟的特性建立历元间约束钟模型用于Kalman滤波接收机钟差估计。实验选取5个IGS站，连续21天观测数据用以模拟实时动态GPS PPP定位，并验证站钟模型对实时动态GPS PPP的影响，实时产品使用CNES发布的CLK93产品。结果表明，目前实时GPS PPP动态定位，在水平面的精度约为2～3 cm，高程方向的精度约为5 cm左右。相比传统的实时GPS PPP动态定位，站钟约束的实时GPS PPP动态定位能有效改善实时PPP高程方向的定位精度，其提高程度约为23.16 %。

动态PPP技术在变形监测、时间传递及水汽监测预报等高精度GNSS地学领域的有着重要的应用，本文方法对于相关领域应用水平的提高具有一定的实际意义。