探究普通学校高中生数学语言转化能力的培养策略

文/广州市广州彭加木纪念中学

在教学实践中，探索培养学生数学语言转化能力的策略，加强数学语言转化能力的教学，是提高学生数学能力的有效途径，也是提高学生数学素养的重要环节，对学生可持续发展都具有深远的意义。

一、重视教师数学语言示范引领和创设学生表达平台，夯实转化能力的基础

在课堂上，教师的语言无疑是学生模仿的对象，也是学生学习数学语言的重要媒介，更是提升学生数学语言转化能力的关键。因此教师要在数学语言上起到示范引领的作用，同时作为课堂的引导者，要善于抓住语言表达时机或者搭建语言阶梯让学生展示，教师只做鼓励者和纠正者即可。能力的形成不是一蹴而就，需要教师持之以恒地有意识加以培养，相信学生能找回用规范的数学语言表达数学问题的自信，从而为数学语言转化能力打下坚实的基础。

二、应用通俗易懂的文字语言化解，促使抽象问题形象化

教师应该依据学生现有的知识背景和心理特征、生活经验等来培养学生的数学语言转化能力。对数学的学习有“畏惧”的情绪，大多数是因数学的本质特征——高度的抽象性所致。教师应该用通俗易懂的文字语言化解抽象问题，当好学生的脚手架，让学生顺利解惑。

例如，在“充要条件”一节新课教学时，有这样一道题：p：00。则p是q的 条件。我引导学生用数轴表示，又从数的角度去说明为什么pq而q不能推出p,部分学生还是有点懵。我就创设一个新的问题问学生：“我是广州人”是“我是中国人”的什么条件？学生很快就说：“我是广州人”当然能推出“我是中国人”，但“我是中国人”就不能推出“我是广州人”。讲完这话时就已然明白“小范围”是 “大范围”的充分不必要的条件了。于是趁热打铁，出招：

(1)设p：11，则p是q成立的( )

A.充分不必要条件

B.必要不充分条件

C.充要条件

D.既不充分也不必要条件

(2)“x<0”是“ln(x+1)<0”的( )

A.充分不必要条件

B.必要不充分条件

C.充要条件

D.既不充分也不必要条件

这次绝大多数学生“接招”顺利。

因此在数学课堂上，面对使用符号语言或图形语言这些抽象问题时会觉得难以理解，使问题更形象化，学生自然能豁然开朗，也就有继续学下去的兴趣和信心。

三、加强概念或公式、定理等的语言转化，深化全面理解

多元表征理论认为，从不同的角度对同一数学对象进行多元表征，可以使数学学习对象多角度得到具体化，能够使数学对象被全面透彻地感知。 数学学习，最基本的知识就是概念、公式、定理等的学习，而这些知识往往都是经过千锤百炼的最规范、最简洁又是高度概括的的数学语言呈现在教材上。在高中的课堂上，需要教师能用多种语言进行引导和整理，帮助学生准确地理解数学问题。把握概念、公式、定理等的本质。

例：等比数列的定义教学案例

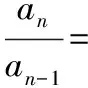
数学概念或公式定理大都有多元表征，因此在这些重要知识的课堂教学中，不仅要让学生记住它的定义或定理，认识表示它的符号，更要从不同侧面突出它的本质特征，构建以其本质属性为纽带的网络结构，深刻理解数学对象，也只有这样才能在不同的情景中根据问题的形式和内容，提取出相应的解决问题的方法和策略。

四、加大数学语言转化在问题解决中的应用，开拓学生思维

数学家哈尔莫斯说过：“问题是数学的心脏。”每一堂数学课都必是学生应用数学语言的相互转化来展示思维并最终解决问题的过程。因此数学语言转换能力在问题解决中的重要性是不言而喻的。

例：定义在R上的偶函数f(x)在[0,+)单调递减，且f(2)=0，则不等式x·f(x)<0的解是____。

答案是(-2,0)∪(2,+∞).

将题意的符号语言f(2)=0转化成文字语言即是函数图像经过(2,0)的点，结合偶函数的对称性，构造符合题意的图像(即是从文字语言与符号语言中转化成图形语言),如下图：

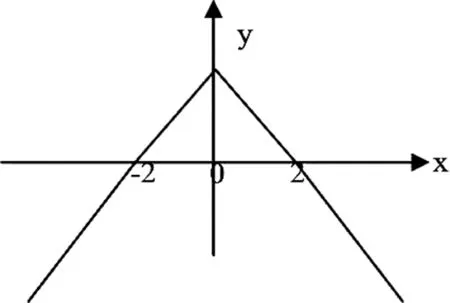
问题解决：将x·f(x)<0的解的符号语言转化成文字语言：横坐标x与纵坐标y异号时的x的范围，即第二、四象限的图像符合题意。此时通过图形语言表达的答案已经“柳暗花明”了。

对于这一问题，学生如果单单是抓住数学符号语言这一项，就会觉得无从下手，思维就会受到限制，如果利用数学语言的互相转换，将这一符号语言转图形就可以方便我们寻找问题的突破口。在图形语言中再用学生颇感亲切的文字语言翻译之，原来看似无解的数学问题便迎刃而解。

文字语言具有亲切感但有时会显繁冗，符号语言精简而显抽象，图形语言形象直观但有时未能使问题具体化。三种语言各有特点，在具体情境或问题解决中又都有其不可或缺的作用。因此，在培养学生数学语言转换能力方面，教师不仅思想上要重视，而且课堂教学中要坚持有目的、有针对性地培养学生三种语言的转化能力，让学生学会将三种语言朝着问题解决的方向进行有目的性的转化，在表达世界时学会能选择恰当的数学语言清晰简洁地表达不同的现实问题，从而提高学生解决问题的能力，提高学生的数学核心素养