基于“直觉表征”“改造”学生经验
朱孟迪
[摘 要]学生在学习之前已经积累了很多有关平行与垂直的感性经验,教师在教学中要利用好这些“直觉经验”,将其改造成学生的“数学经验”。教学“平行与垂直”时,按照“先体验、再实践、后概念”的教学顺序,引导学生展开思考与实践。
[关键词]平行垂直;改造经验;实践思考
[中图分类号] G623.5[文献标识码] A[文章编号] 1007-9068(2019)29-0063-02
“平行与垂直”是人教版教材四年上册“平行四边形和梯形”单元起始课。教材基于“图形分类”的方式编排:在白纸上任意画两条直线——对两条直线的位置关系分类——认识平行与垂直。这种方式有一弊端,学生所画的平行线不能突显其本质,换句话说,平行线很难画,稍一偏差就是相交(教材已取消平行线的作图要求)。因此,教师可通过改造“学习材料”——借助方格纸让学生“直觉表征”,逐步剥离学生“错误的”“偏差的”“非本质的”经验,帮助学生形成正确的认知。
一、发挥经验,改造经验
师:这是一张白纸,把它看作一个平面,请你展开想象,这个平面可以变得——无限大,我们就要在这个平面内研究直线与直线的位置关系。
1.画出心目中的“平行”与“垂直”
师:想一想,平行是怎样的?垂直呢?想好了吗?请在方格纸上分别画出你心目中的平行与垂直。(学生操作,教师收集作品)
2.交流“平行”——基于经验,改造经验
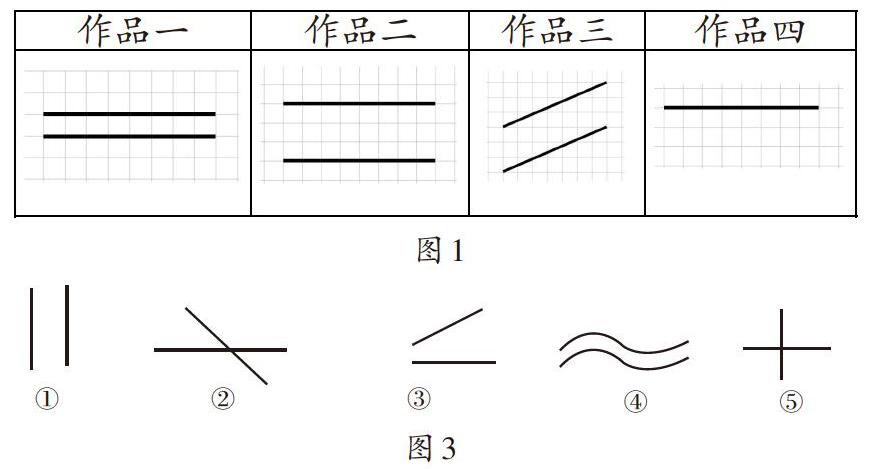
学生作品:
师:作品一符合你心目中的平行标准吗?
生1:平平的线就是平行。
生2:这两条直线的中间都是1格,像这样,中间都是1格1格的,即使无限延长后也不会碰在一起。
师:像这样无限延长后也不会碰在一起的两条直线就是平行,对吗?既然这样,作品二呢?
生3:因为中间都是3格,所以无限延长后它们仍然不会碰在一起。
师:你们都说无限延长,如图2这样延长,它们还是不是平行,为什么?
生4:直線可以无限延长,长一点短一点都没有关系。
生5:只要不碰在一起就可以。
师(转动方向,图略):你认为这样还是平行吗?
生6:还是平行,因为它们还是不会碰在一起。
师:对,即使改变方向,只要不碰在一起,你们还认为是平行的。
师:作品四中只画了一条直线,这是平行吗?显然不是。如果给它加一条直线变成平行,该怎么画?
师:看来,你们心目中的平行是指两条直线的位置关系。
二、丰富表象,形成平行概念
1.在辨析中丰富表象
生1:①号是平行的,因为无限延长也不会碰头。
生2:②号不是平行的,两条直线相交了。
师:我们把②号这样的位置关系称为两条直线相交,相交的点称它为交点。对于①号的两条直线,我们可以称它为不相交。
师:③号、④号的两直线也没有相交,它们应该算平行吗?
生3:③号的两条直线向左延长后会相交。④号是两条曲线,不是直线。
2.建构平行的概念
师:“在同一平面内不相交的两条直线叫作平行线,也可以说这两条直线互相平行。”想一想,为什么要在“平行”前面加上“互相”两字?
生4:只有一条是不够的,平行是两条直线的一种位置关系。
师:如果一条直线记作直线a,另一条直线记作直线b,于是可以说“直线a是直线b的平行线,直线b是直线a的平行线,它们互相平行。”为了表示方便,数学上还给平行用了上符号——“a[?]b,读作a平行于b。”你看,这个符号多像平行哪。请在草稿纸上表示出自己作品中的平行,并读给同桌听吧!
三、基于经验,形成垂直概念
1.在比较中引入“垂直”
师:让我们把目光聚焦到这些相交的情况。你感觉哪两条直线最特殊?为什么?
生1:⑤号(图3),因为4个角都相等,都是直角。
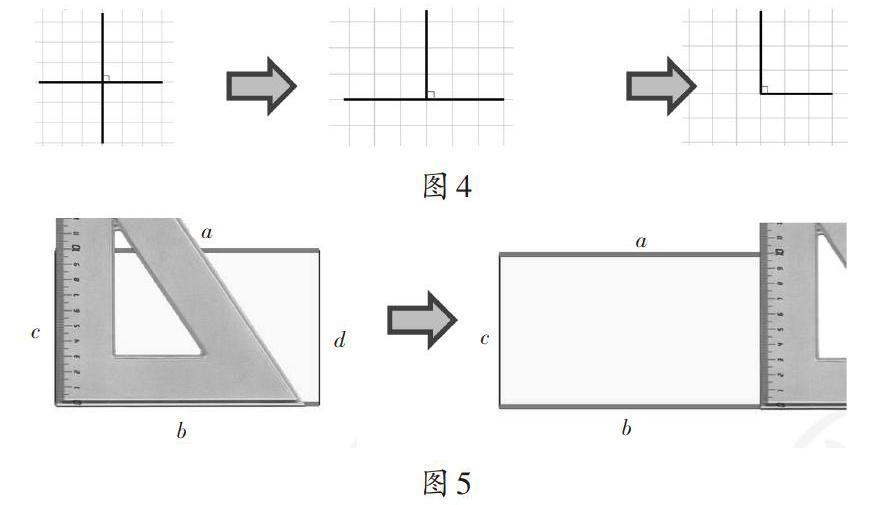
师:要知道是不是直角,得借助三角尺来验证。
2.形成垂直的概念
师:在数学上,如果两条直线相交成直角,就说这两条直线互相垂直。其中一条直线叫作另一条直线的垂线。如果给这条直线取名为直线a,另一条直线取名为直线b,你怎么理解这两条直线的位置关系呢?
师:现在把这组互相垂直的直线旋转方向,再转动,现在它们还是互相垂直的吗?为什么?
师:在数学上,互相垂直的两条直线还可以用这样的符号表征——“直线a与直线b互相垂直,记作a⊥b,读作a垂直于b。”
3.判断中理解垂直的本质
师:我画了一些垂直的情况,你有什么新发现?
四、拓宽经验,沟通联系
师:在同一平面内两条直线的位置关系会有几种呢?
师:现在让我们一起来整理。在同一平面的两条直线只有两种情况,一种是不相交,也可以称它为互相平行;另一种是相交,如果相交成直角,它们就互相垂直;如果相交成钝角、锐角,就称它们普通相交。
五、应用经验,解释现象
师:你在生活中看见过平行或垂直吗?这是两条线段a、b(如图5),你怎么知道它们是否平行?
师:有没有互相垂直的?为什么说它们互相垂直?有几组垂直?你对长方形又有了怎样的新认识?
师(出示一张不规则的纸片):这张纸上有平行吗?垂直呢?你能创造出一个垂直吗?是的,这是我们二年级学习直角时折纸的方法。为什么两次对折后就是直角了呢?
生1:把360°对折一次就是180°,对折两次就是90°了。
师:如果按这样的方法在另一个位置上再折一次,你有什么新的发现?
生2:垂直于同一条直线的两条直线互相平行。
六、回顾反思,总结经验
本节课基于学生的“经验”改造学生的经验,以帮助学生形成正确的“认知结构”,主要体现在以下三点:
1.改造“平行”经验,遵循“先体验、再实践、后概念”的原则
(1)先体验。课始,确定本课的学习范围——在同一平面内。学生根据自己的经验尝试画出心目中的“平行”,教师通过“改造”学生的“作品”,帮助学生完善对概念本质属性的理解。“改造”中突出以下几点:①平行线之间的格数保持不变,突显平行线之间的距离处处相等的本质;②改造成“一條线长,另一条线短”的视觉效应,突出平行线的本质实则为“直线”,与其长短无关;③改变平行线的方向,借助旋转变化,突显“只要两条直线不相交”的本质。一次次的经验改造,一次次的思维冲突,打破了非本质因素对概念建构的影响,进而把学生的思维聚焦于本质属性上。
(2)再实践。对于教师出示的一组“判断素材”,学生借助直观经验,借助之前的讨论辨析,很容易找到“平行”。同时,“平行曲线”的学习素材也丰富了学生对平行概念本质的理解。
(3)后概念。通过“先体验”与“再实践”,学生头脑中已经有了丰富的平行表象,平行的概念呼之欲出,教师只需要顺势利导,呈现概念即可完成教学目标。
2.改造“垂直”经验,打破学生思维定式
(1)借助判断,突破难点。一方面,以“垂下来的线”为素材展开教学,让学生知道数学中的垂直是两条直线的位置关系,以回应学生“心目中的垂直”。另一方面,学生辨别一般的“垂直”几乎没有问题,但对于“丁字型”或“直角型”的垂直的理解往往存在困难。然而,借助直观演示与争论,学生就把思维聚焦于“两条直线”,进而很好地说明了问题,突破了难点。
(2)沟通联系,形成体系。以“快速判断”两条直线的位置关系为载体,一方面让学生理解垂直是一种特殊的相交,另一方面帮助学生形成两条直线位置关系的框架结构。
3.改造学习经验,拓展知识外延
直线是抽象存在的。学习了本节课的知识,学生对长方形就有了新的认识,如“长方形对边平行”。而借助尺子度量让学生直观看到“这两条线段之间的距离都相等”,即便无限延长也不会相交。至此,学生成功借助学习经验来解释了现实生活。
(责编 金 铃)

