改进学具，让计算的意义和逻辑更明确

金干周

[摘 要]数数本身就是一个对物理量进行度量的过程，数字则是对物体按照1个单件为标准进行度量后得出的数学化符号，先有量后有数。计算时，往往只体现数字变化，没有体现量的变化，而通过改进学具，可以让计算的意义和逻辑更明确。

[关键词]数数;度量;数量;改进学具

[中图分类号] G623.5[文献标识码] A[文章编号] 1007-9068（2019）29-0035-02

数学是研究数量关系的一门学科，可是小学数学中并没有阐述清楚何为数，何为量。例如，算式2+3=5中的数字2，3，5各代表什么含义？该算式可以解决哪些问题？做对就能会用吗？如何检验对错？算理是什么？对于这些疑问，教材中并没有明确的解答。为了让知识更严密，让学生从小形成推理意识，笔者就数与量的教学谈一些粗浅的认识。

一、数数是一种度量，要分清数与量的关系

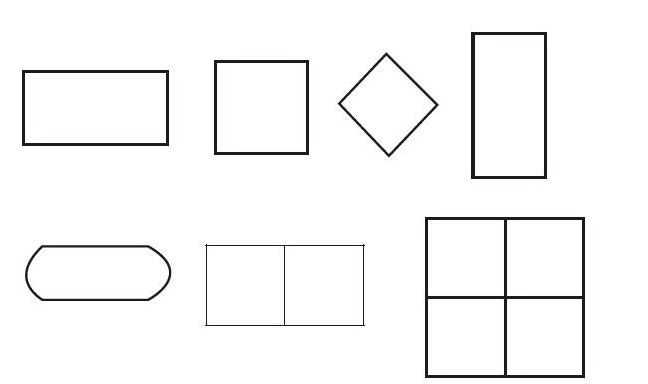
万事万物都有质和量。质决定了事物的物理化学属性，量却反映了多少。究竟何为量呢？任何事物都能用自己的一部分作为标准去度量整体的容量。事物的这种自定义可测性就是量化，即量指的是事物的大小、范围、程度等。用一个基本量度量时就会产生次数，度量次数抽象出来就是数字。由此可见，数是从度量中提炼出来的，先有量，后有数。事实上数数就是一种度量，是用“一个”作为标准去度量，看整体含有多少个这样的“一个”。只不过这种度量不需要借助计量工具，只需要进行数目比对。例如，数数下列各图中共有多少个正方形。

在清点正方形时，从第一个图形开始，用一个正方形的形状去对比，通过形象对比发现：只有第二、第三、第七个图形符合标准，于是只有3个图形满足有正方形这个条件。再如，一桶食用油重5千克，对这个数字的理解应是：把一千克油的重量作为标准去度量一桶油，正好分出5份;而不是一次性称量出一桶油的重量是5千克。因为如果这桶油里含有杂质，或者秤有问题，虽然读数是5千克，但实际上净重仍未达到5千克。这就是说，称重本质上是一种简化的度量法。

由“数是由度量产生的”就可以厘清数和量的关系：“数”是对“量”的抽象化和符号化处理，它是人为规定的。“量”是客观存在的物理特征，不可更改。因此同一个量，可以用不同的数字和度量单位来表达。例如，1米长的量可以有多种表示方式：1米、10分米、100厘米、0.001千米，还可以表示为3尺。数和量，后者是实物，前者是名称。数必须通过度量才能计算出来，量则是不会随着度量行为和度量标准的改变而改变。

二、分清自然数“1”与“单位1”的区别

厘清了数和量的关系，也就不难理解“自然数1”与“单位1”的区别。“单位1”的提出是为分数意义教学做准备的。“单位1”的定义以及与“自然数1”的区别和联系，课本和教参中语焉不详。学生对二者的区别大多一知半解。区分数和量是区分二者的基础。“单位1”是指度量前一个抽象的度量单位，是客观存在的。“自然数1”是指度量时一个度量单位出现的次数，只有度量行为发生时才会出现。“单位1”是静态事实，“自然数1”是动态产生的。“单位1”属于量，“自然数1”属于数。

明确了数和量的关系，就要对算式中的各个数字规定其意义。一个不带单位的数学算式，其中的数字表示的究竟是数，还是量？这需要说明，否则无法计算。因为数只是一种对量的抽象记录的文字符号，文字符号是没有大小的，是无法计算的，所以算式中的数字必须是物理量。然而算式中的数字必须赋予其物理意义，否则无法判断对错。例如2+3=5，该式子如果脱离物理量，则无法判断对错。因为只要是用同一个度量单位度量了两次，都能抽象为“2”，同理，凡是用同一个度量单位度量了三次，都能抽象为“3”。试想：2根黄瓜与3个鸡蛋合起来能等于5根香肠吗？2年加3天能等于5秒吗？判断的理由是什么，推算过程是怎么样的？这些都不能仅凭直觉，而必须对每一个数字赋予其物理意义，并且还要建立评判标准。可是现在的小学数学教学中，没有严格规定数的意义，因此也就缺乏判断对错的标准。可见，当下的小学数学教学中，存在着“数量不分、逻辑不严”的弊端。

三、学具的运用不当导致算式中数字的无意义化

传统的计数学具，如小棒、方块计数器、点子图等，都没有体现数字的度量属性，不具有代表性，无法揭示数与量的转换关系。尽管学生也能借助这些工具理解数的意义，但无法明确数的度量属性，厘不清数和量的关系，若盲目粗暴地给算式中的数字赋予物理意义，根本无法让其成为一般规律。要实现预定目标，必须创新计数学具。要体现“数是由度量产生的”这一规律，计数学具首先应该具有直观的可度量性，其次还应具有可替换性。而常规的小棒、计数器、点子图却缺少这两大功能。

四、方格认数学具能正确体现计算中数的意义

什么样的学具正好具备可度量性和可替换性这两大功能呢？它就是方格认数学具。方格认数学具是用方格代表实物个数，用图片代替实物，通过动手操作实验来完成计数的一种学具，它适用于小学各个学段。方格认数学具中的方格里面包含图片信息，它不但可以形象代表各种物体，还能很好地将现实数量问题通过“实物图片—方格—数量”的方式转化成数学问题，然后通过实验操作来解答，最后通过方格数来验算。由于方格中有图片，图片上的信息直观形象，使用方格时可以通过想象完成演算。对于一个不带物理单位的算式，也可以统一设定判定标准：算式中的数字表示一个可以代表任何物體的方格数量，它的对错判定标准，就是是否与方格移动操作的实验结果相符。做应用题时，再把方格中的图片替换成题中所设的事物，然后再根据度量单位的一致性来判断算式的合理性。如此一来，就顺利实现了一般算式可用实验操作法来判断对错。由于方格内容的万能性，用方格认数学具计算时，也实现了数字物理意义的万能性，同时纠正了用特例当作普遍规律的错误。有了用方格代表个数和用方格内图片代表实物的思维转换过程，再根据研究数量关系的基本原则（①客观事物的数量可以用图片代替实物;②事物的数量与实物所处的位置无关）可以让计数教学变得明朗起来。例如，数字2默认表示2个方格，数字3默认表示3个方格，2+3=5就表示2个方格加3个方格等于5个方格，这样就不会产生歧义。如果涉及应用题，就必须在方格中填充图片，把图片想象成实物，再联系实际进行计算。此外还必须明确，只有统一图片内容，式子才能成立，否则将无法计算。这就给数字符号赋予了确定的物理意义，建立了判断标准。数学计算对错的评判标准，是一个实践检验过程，以客观事实为唯一依据。

方格认数学具的一个方格包含一张图片，内容可以是任何单个物体，也可以是多个同类的物体组合的整体;可以是照片，也可以是图画;可以是实物，也可以是虚拟物体。但不论表示何物，数字“1”都表示度量次数。而“2”必须是用同一个度量单位度量了两次才能记作2，不是随便将两个“1”合并为“2”。也就是说，如果不对数字规定其具体的物理意义，那么1+1=2未必就对。

（责编 罗 艳）