几何直观在小学数学教学中的应用

陶春鸽

[摘 要] 在小学数学学习中，解决数学问题一直是困扰学生的难题，有时学生在解题过程中无从下手。几何直观能力是数学核心素养之一，在数学课堂教学中，有效运用几何直观教学，能生动形象地展示数学问题的本质，让数学问题由抽象变具体，极大地提高了学生的数学思维能力。

[关键词] 小学数学;几何直观;应用;课堂教学

几何直观是指借助几何图形的形象关系激发学生对抽象事物的直观感知，即利用图形语言将复杂的问题简单化，帮助学生更好地解决数学问题，培养学生的创新思维和实践能力。几何直观不仅是一种学习方法，更是一种学习能力，具体表现为学生运用图形语言思考问题的能力、思维发散能力和洞察能力等。

一、借助直观图示培养形象思维

“形象思维”又被称为“直感思维”，这种思维形态将具体的图形作为思想内容，有利于发展小学生的几何直观。几何直观指根据图像的直接特点，把直接观察到的图形表面现象与抽象的数学问题结合起来，即结合形象思维与抽象思维表现问题本质，培养儿童独立思考的能力。通过“直观模型”不仅有利于提升儿童思考问题与分析问题的积极性，而且可以促进儿童思维能力的发展。

1.化复杂为简单

在引导学生进行数学学习的过程中，借助直观图示能够达到化复杂为简单的效果。

例如，在“打电话”一课的教学过程中，教师在上课前提出问题：星期天，李老师需要让7位学生到学校，如果采用打电话通知学生来学校的方式，通知一位学生需要1分钟，那么怎样能够快速地通知所有的学生呢？通知全部学生需要多长时间呢？请每位同学大胆思考一下。教师刚抛出问题，学生们就开始探讨起来，得出的答案分别有“7分钟、6分钟、1分钟”，等等。同时，教师提出引导问题“这么多答案，到底哪一个是正确答案呢？哪位同学能够证明一下自己的答案是正确的呢？”然后教师采用示意图的方法将抽象问题具体化，引导学生自主思考。

大部分学生在描述自己的思考过程时，都采用了图示法（如图1）。

这样就能够简单地呈现出复杂的数量關系。同时学生在示意图中还能发现一些其他的规律，比如：第二分钟以后，接收到通知的人数是前一分钟的2倍。教师在教学的过程中，引导学生采用直观图示描述通知电话的过程，辅助学生思考问题。学生们采用直观的学习方法找出问题的答案，提升自己的形象思维能力。

2.化模糊为清晰

几何直观能把复杂的数学问题用最直观的方式展现出来，从而引导学生深入思考问题。绘制图形属于直观体验，有利于培养学生的几何能力，因此培养学生几何直观能力的最根本方法是培养学生绘制图形，以此培养绘制图形的能力。教师应鼓励学生绘制图形，让学生明白绘制图形的根本并不在于形似，而是在于帮助自己梳理逻辑，理解问题。

例如，在“倍的认识”一课的教学过程中，教师可设置森林舞会活动的教学情景，“小老虎的数量是小狮子的2倍，小兔子的数量是小老虎的2倍”。然后引导学生使用自己喜欢的图形代替森林中的动物，表示出其中的倍数关系加以计算。由此，教师轻松地将具体数字与倍数联系起来，也有助于学生理解“倍数”。最重要的是学生在学习的过程中可根据自己的喜好选择相关的元素，引导学生积极学习与主动学习。

二、借助直观操作发展直观思维

直观思维是指一种可以不经过人们逐步分析，根据现象快速地做出合理性猜测的思维。跳跃性是直观思维与几何直观共有的特点，但直观思维是在切身体验中培养出来的。因此，教师在教学的过程中应为小学生提供大量可供操作的机会，让学生的多个感官同时参与到学习的活动中，以此来培养他们的直观思维。

1.建立知识体系

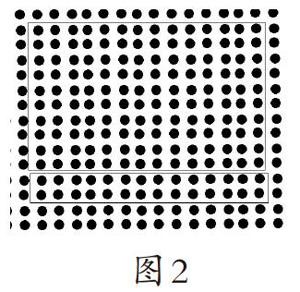
例如，在“两位数乘两位数”的教学过程中，一位教师首先提出问题：“一套书共14本，李老师一次买了12套，估算一下李老师共买了多少本书呢？”教师引导学生估算书本数量后，应进一步提出问题“能够算出李老师共买了几本书呢？”然后，教师应引导学生使用点子图（如图2）计算购买的书本数量，同时记录下自己思考的过程。学生在自己动手的过程中，直接地发展了自己的直观思维。

2.引导自主探究

在小学数学课堂上，教师可以引导学生在直观操作中进行自主探究，以此促进他们数学探究学习的高效化。

几何直观的本质是指根据图形激发学习者的想象力，利用图画简化并解决数学问题。因此教师在教学的过程中应善于创设教学情境，培养学生绘制图形的能力和几何直观能力。

三、借助数形结合发展图形语言

华罗庚先生曾说过：“形缺数时难入微，数缺形时少直观。”可见其对数形结合的重视。数形结合能将抽象的数学概念具象化，给人更直观的感受，能够在一定程度上降低小学生对数学的理解难度，能够无形中提升小学生图形语言能力和图形推理能力。

例如，在“植树问题”一课的教学过程中，教师可以提出这样的问题：六年级的学生在一段长为1000米的小路上植树，如果每棵树的间隔是10米，请猜猜要栽多少棵？有的学生回答100棵，也有的学生回答99棵，还有学生回答101棵，大家的意见并不统一。这时，教师建议学生们想办法验证一下自己的猜想。有学生提出，先将题目简化为在长为20米的小路上植树，间隔10米一棵，一共要栽3棵;如果是在50米的小路上植树，应该栽6棵;还有学生画出10厘米的线段图来表示自己的想法，每隔1厘米画一个线段，然后数线段上的点得出结果。

在这个教学案例中，教师鼓励学生将自己的思维方式转化成图形语言来解答，将抽象的问题直观化，然后从图形中提取信息，找出其中的数量关系，那么问题也就迎刃而解了。

综上所述，几何直观贯穿于整个小学数学学习中，它能将隐蔽的问题明朗化，对学生数学学习帮助很大。教师在教学中可以从多角度开展几何直观教学，结合经典例题的讲解，将理论与实践结合起来，拓宽学生解题思路，引导他们用几何直观进行多解法解题，潜移默化提升学生数学综合能力。

参考文献

[1] 冯崇和. 几何直观：探索解决小学数学问题的重要手段[J]. 内蒙古师范大学学报（教育科学版），2014，（08）.

[2] 孔凡哲，史宁中. 关于几何直观的含义与表现形式——对《义务教育数学课程标准（2011年版）》的一点认识[J]. 课程·教材·教法， 2012，（07）.

[3] 蒋碧云. “借形解数”：进一步发展学生的几何直观能力——“解决问题的策略——转化”教学有感[J]. 云南教育（小学教师）， 2016，（11）.

[4] 何红亚. 发挥几何直观在数学理解中的作用——以四年级下册《用画图的策略解决相遇问题》为例[J]. 教育研究与评论（小学教育教学），2012，（08）.

责任编辑 王   慧