要素资源错配、所有制结构与技术创新

吕承超 王志阁 王媛媛

摘 要：作为企业创新活动的基础，要素资源对高技术产业上市公司技术创新可能产生重要影响。本文构建理论模型，利用2012—2016年我国高技术产业上市公司微观数据，建立动态面板模型，采用系统GMM估計方法分析要素资源错配对技术创新的影响。研究结果显示：技术创新存在明显的循环累积效应;资本错配对医药制造业和铁路、船舶、航空航天及其他运输设备制造业上市公司技术创新分别有负向影响和正向影响，且存在非线性相关关系;劳动力错配对高技术产业上市公司的技术创新投入或技术创新产出有显著正向影响，且存在非线性相关关系;资本错配和劳动力错配对某些行业和地区高技术产业上市公司技术创新的影响有显著的所有制差异;控制变量中，资本密集度有利于技术创新水平的提高，有形资产率则对技术创新有抑制作用。

关键词：要素资源错配;所有制结构;技术创新;系统GMM

中图分类号：F062.9  文献标识码：A

文章编号：1000-176X（2019）10-0044-09

一、问题的提出

改革开放40年，我国经济取得了举世瞩目的成就，经济总量已经跃居全球第二位。我国经济的高速增长主要依赖于制度红利、人口红利和环境红利等，然而，随着人口老龄化程度加剧、要素成本增加和环境约束增强等原因，我国经济进入到了新常态。经济新常态下，一方面，金融市场摩擦可能导致企业之间资本配置的扭曲，造成资本错配问题;另一方面，劳动力市场受到体制干预，可能导致劳动力错配问题。要素资源错配是相对有效配置而言的，错配即是对帕累托最优状态的偏离，资源错配表现在不同产业或不同企业之间边际产品价值不相等。由于我国市场体制不完备、所有制歧视和政策诱导等因素，各地区要素市场的改革进程滞后于产品市场的改革进程，要素市场扭曲问题比较突出，要素资源错配现象依然严峻[1]。在经济新常态背景下，如何理清要素资源错配，把握要素资源错配对技术创新影响的作用机制，已经成为亟待研究的问题。

目前国内外关于要素资源错配或要素市场扭曲的研究多集中于对全要素生产率（TFP）的影响上，得到的结论也不尽相同。大部分学者认为要素资源错配或要素市场扭曲对TFP的提升具有阻碍作用。Hsieh和Klenow[2]通过对比中国、印度和美国的TFP水平指出，如果中国和印度的资源配置效率达到美国的水平，其TFP水平可分别提升30%—50%和40%—60%。由市场不完全导致的企业间资源错配造成了TFP的实质性差异，进而阻碍了经济增长[3]。很多学者的研究表明，若能减少要素资源扭曲，有效改善要素资源错配状况，即使在不增加投入的前提下，我国的 TFP 或GDP水平也将得到大幅度的提升[4]。资源配置效率成为制约我国TFP提升的首要因素。也有部分学者认为要素资源错配或要素市场扭曲对TFP造成的影响很小，要素资源错配对TFP损失或差异的解释只能占很小一部分，而要素再配置效率不仅非常低[5]，而且对全要素生产率的提升作用很小[6]，资源配置不存在显著的结构红利效应[7]。此外，有部分学者的研究涉及要素市场扭曲与创新的关系方面。有学者从不同角度研究了金融发展与技术进步之间的关系，指出高效的金融市场有助于经济主体创新活动的开展[8]，创新资源的合理分配对技术创新尤为重要[9]。然而，我国要素市场的市场化进程滞后导致了要素市场扭曲，阻碍了企业R&D投入的增加[10]，使得企业所需要的创新资源无法得到满足，这不仅会抑制创新效率的提高，也不利于我国市场主体自主创新活动的开展[11]。

综上所述，虽然学术界关于要素资源错配与TFP的关系展开了广泛研究，但关于要素资源错配对技术创新影响的研究不足，不仅未取得一致的结论，并且以往研究缺乏必要的数理模型推导，多侧重于采用宏观数据检验，相关结论缺少微观数据的实证支持。基于此，本文拓展Hsieh和Klenow[2]与戴魁早和刘友金[12]的生产率误置模型，对要素资源错配与技术创新的关系在理论上进行了推导，并利用我国高技术产业A股上市公司的数据，选取相关指标，基于全部样本、分行业、分地区、分所有制对理论模型进行实证分析并进行稳健性检验。本文创新之处在于：其一，构建理论模型，为要素资源错配与技术创新之间可能存在的关系提供理论依据，这是对现有文献的补充。其二，丰富技术创新影响因素的研究领域，扩展技术创新影响因素范畴。

二、理论模型

（一）基本条件假设

假定一个垄断竞争的市场结构，设定代表性厂商i的柯布—道格拉斯函数：Yi=AiLαiKβi，其中，Yi为代表性厂商i的产出，Ai为技术创新水平，Li为劳动力数量，Ki为资本存量，α和β分别为劳动力和资本的产出弹性系数，假定α+β=1，即代表性厂商规模报酬不变。

在经济发展过程中，存在政府和信贷对国有企业扶持倾斜、劳动力和资本等资源价格扭曲及要素市场分割等现象，可能导致资源错配问题包括资本错配和劳动力错配两个方面。为了测算实际要素价格与竞争性价格之间的偏离程度，本文定义劳动力错配指数τLi和资本错配指数τKi，分别表示劳动力错配程度和资本错配程度。τLi和τKi的取值范围在-1—1之间，τLi和τKi越小，表示要素资源错配程度越低，反之则越高。定义wi和ri分别为劳动力市场和资本市场的竞争性价格。由此，wi（1+τLi）和ri（1+τKi）分别表示劳动力错配价格和资本错配价格，则代表性厂商i的利润函数为：

πi=PiYi-wi（1+τLi）Li-ri（1+τKi）Ki（1）

其中，πi为厂商i的利润，Pi为厂商i的产品市场价格，假定厂商被动接受产品市场价格。当τLi=0、τKi=0时，表示要素市场不存在资源错配问题，要素市场价格为竞争性价格，厂商获得正常利润;当τLi>0或τKi>0时，表示存在资源错配问题，竞争性价格低于要素市场价格，厂商承受要素市场价格高估造成的利润损失;当τLi<0或τKi<0时，表示存在资源错配问题，竞争性价格高于要素市场价格，厂商可获得要素市场价格低估带来的超额利润。

（二）基本模型

1.消费者

假定某行业有n家厂商，均生产单一产品，当市场出清时，消费者获得的CES效用函数为：U（Y）=[∫n0Yi（σ-1）/σdi]σ/（σ-1），Y为行业出清时的总产出，Y=∫n0Yidi，σ>1，消费者对代表性厂商购买支出为PiYi，定义Q为消费者对所有厂商的产品总支出，则：

maxU（Y）=max[∫n0Yi（σ-1）/σdi]σ/（σ-1）（2）

s.t.∫n0PiYidi≤Q （3）

式（2）和式（3）分别为消费者的效用最大化函数和预算约束条件，为求得消费者效用最大化时的产出Y，进一步构建拉格朗日函数为：

ω1=[∫n0Yi（σ-1）/σdi]σ/（σ-1）-λ（∫n0PiYidi-Q）（4）

则式（4）的一阶条件为：

ω1/Yi=σ/（σ-1）[∫n0Yi（σ-1）/σdi]σ/（σ-1）-1（σ-1）/σYi（σ-1）/σ-1-λPi=0（5）

ω1/Yj=σ/（σ-1）[∫n0Yi（σ-1）/σdi]σ/（σ-1）-1（σ-1）/σYi（σ-1）/σ-1-λPi=0（6）

由式（5）和式（6）可得：

Yi/Yj=（Pi/Pj）-σ（7）

對式（7）两边同乘以Pi得：PiYi/Yj=Pi1-σ/Pj-σ，进一步积分：

∫n0PiYidi/Yj=∫n0Pi1-σdi/Pj-σ（8）

将价格指数P=（∫n0Pi1-σdi）1/（1-σ）定义为CES加总价格，则将其代入式（8）得：

Yi=QPi-σ/P1-σ（9）

式（9）表明，消费者效用最大化时，消费者的总支出、代表性厂商i的产品价格和加总价格共同决定了消费者对代表性厂商i的产出需求量。

2.厂商

厂商总成本TCi由可变成本MCiYi和固定成本FCi之和构成。长期生产中，所有要素均可随产量变动，则厂商总成本TCi为MCiYi，等价于wi（1+τLi）Li+ri（1+τKi）Ki，则在消费者效用最大化条件下，代表性厂商i利润最大化问题为：

maxπi=max（PiYi-MCiYi）（10）

s.t.Yi=QPi-σ/P1-σ（11）

代表性厂商利润最大化的一阶条件为：Pi=σ/（σ-1）MCi，表明代表性厂商i产品价格是其边际成本的函数，但由于边际成本现实中难以获取，本文考虑代表性厂商i产出既定（设定为Y0）条件下的成本最小化问题，来推导其边际成本：

min [wi（1+τLi）Li+ri（1+τKi）Ki]（12）

s.t.AiLαiKβi≤Y0 （13）

进一步构建拉格朗日函数：

ω2=wi（1+τLi）Li+ri（1+τKi）Ki-λ（AiLαiKβi-Y0）（14）

代表性厂商i成本最小化的一阶条件：

ω2/Li=wi（1+τLi）-λαAiLiα-1Kβi=0（15）

ω2/Ki=ri（1+τKi）-λβAiLiα-1Kβi=0（16）

ω2/λ=-（AiLiαKβi-Y0）=0（17）

由此可得，代表性厂商i既定产出Y0下成本最小化时劳动力和资本的投入：

Li=（Y0/Ai）1/（α+β）[αri（1+τKi）/βwi（1+τLi）]β/（α+β）（18）

Ki=（Y0/Aj）1/（α+β）[βwi（1+τLi）/αri（1+τKi）]α/（α+β）（19）

则代表性厂商i的总成本TCi=MCiYi=[（α/β）β/（α+β）+（α/β）-α/（α+β）][wi（1+τLi）]α/（α+β）[ri（1+τKi）]β/（α+β）（Yi/Aj）1/（α+β），在规模报酬不变条件下（α+β=1），TCi=MCiYi=[（α/β）β+（α/β）-α][wi（1+τLi）]α[ri（1+τKi）]βYi/Aj。那么，代表性厂商i的边际成本：

TCi/Yi=MCi=[（α/β）β+（α/β）-α]（1/Ai）[wi（1+τLi）]α[ri（1+τKi）]β（20）

将式（20）代入Pi=σ/（σ-1）MCi可得：

Ai=σ/（σ-1）[（α/β）β+（α/β）-α]（1/Pi）[wi（1+τLi）]α[ri（1+τKi）]β（21）

式（21）表明，代表性厂商i的技术创新水平Ai与劳动力错配指数τLi和资本错配指数τKi相关。

3.要素资源错配对技术创新的影响

对式（21）分别求劳动力错配指数τLi和资本错配指数τKi的一阶导数：

Ai/τLi=σ/（σ-1）[（α/β）β+（α/β）-α]（1/Pi）αwi[wi（1+τLi）]α-1[ri（1+τKi）]β（22）

Ai/τKi=σ/（σ-1）[（α/β）β+（α/β）-α]（1/Pi）[wi（1+τLi）]αβri[ri（1+τKi）]β-1（23）

由式（22）和式（23）可知，Ai/τLi、Ai/τKi均大于零，表明要素资源错配指数τLi、τKi与代表性厂商i的技术创新水平Ai之间均呈现单调递增的关系，即随着要素资源错配程度的提高，代表性厂商的技术创新水平也会提高，反之则降低。当τLi>0、τKi>0时，代表性厂商要素使用价格高于竞争性价格，厂商遭受利润损失，此时，厂商愿意通过提高技术创新水平来增加产品附加值，弥补由资源错配造成的利润损失;当τLi<0、τKi<0时，代表性厂商要素使用价格低于竞争性价格，可以获得要素市场价格低估带来的超额利润，此时厂商缺乏技术创新的动力。

为进一步明确要素资源错配对技术创新水平的具体影响效果，在式（22）和式（23）的基础上，进一步求劳动力错配指数τLi和资本错配指数τKi的二阶导数：

2Ai/τLi2=σ/（σ-1）[（α/β）β+（α/β）-α]（1/Pi）α（α-1）w2i[wi（1+τLi）]α-2[ri（1+τKi）]β（24）

2Ai/τKi2=σ/（σ-1）[（α/β）β+（α/β）-α]（1/Pi）[wi（1+τLi）]αβ（β-1）r2i[ri（1+τKi）]β-2（25）

由式（24）和式（25）可知，2Ai/τLi2、2Ai/τKi2均小于零，由于Ai/τLi、Ai/τKi均大于零，可知式（21）是一个单调递增的凸函数，且其斜率逐渐递减。

三、研究设计与回归分析

（一）变量选取与模型设定

1.变量选取

（1）被解释变量：对技术创新的度量主要集中在投入、过程和产出三个角度。鉴于过程测度的指标多为定性指标且偏重于对组织机制方面的研究[13]，本文将从技术创新投入（tii）和技术创新产出（tio）两个维度衡量企业技术创新（ti），用研发资金投入与员工人数的比值衡量技术创新投入，用专利授权数鉴于外观设计几乎没有技术含量，本文用发明专利和实用新型数量加总衡量专利授权数。与员工人数的比值衡量技术创新产出。

（2）核心解释变量：要素资源错配（frm）包括资本错配（krm）和劳动力错配（lrm）。本文参照邵挺[14]的方法，资本错配程度以每个企业资金使用成本与所在行业平均资金使用成本的偏离程度衡量，其中企业资金使用成本以利息支出除以扣除了应付账款后的负债总额衡量。

根据会计准则，企业应付账款不需要支付利息，因而应从负债总额中予以扣除。劳动力错配程度以每个企业劳动力使用成本与所在行业劳动力平均使用成本的偏离程度衡量，其中企业劳动力使用成本以企业支付给职工以及为职工支付的现金与员工人数的比值衡量。

（3）控制变量：基于企业异质性理论[15]，本文主要加入企业规模（size）、企业年龄（age）、资本密集度（cap）、杠杆比率（lev）和有形资产率（rta）等控制变量。本文以企业资产总额衡量企业规模，以企业成立至样本年份的经营年限衡量企业年龄，以企业固定资产净值与员工人数的比值衡量资本密集度，以企业负债总额与资产总额的比值衡量杠杆比率，以企业固定资产净额与资产总额的比值衡量有形资产率。

为了考察不同所有制性质企业要素资源错配对技术创新的影响，按所有制性质（own）划分为国有企业和非国有企业，国有企业赋值为1，非国有企业赋值为0。同时，本文引入要素资源错配与所有制性质的交互项，包括资本错配与所有制性质的交互项和劳动力错配与所有制性质的交互项。为了控制不同年度宏观经济环境和政策变动[16]对技术创新的影响，本文还引入年份哑变量。

2.模型设定

对理论模型式（21）两边取自然对数得：

lnAi=lnσ/（σ-1）[（α/β）β+（α/β）-α]+ln（1/Pi）+αlnwi+αln（1+τLi）+βlnri+βln（1+τKi）（26）

其中，Pi、wi和ri分别为产品市场和要素市场的竞争性价格，可将计量模型简化为：

lnAi=α0+α1lnτLi+α2lnτKi+∑βicontroli+εi（27）

其中，α0为常数项，α1和α2分别为劳动力错配系数和资本错配系数，βi为控制变量系数，controli为各控制变量，εi为随机误差项。

根据缪尔达尔的循环累积因果理论，在经济社会动态发展过程中，前期技术创新可能通过回波效应和扩散效应影响当期技术创新，因而在计量模型中加入技术创新的滞后期。此外，要素资源错配对技术创新具有边际效应递减趋势，因而在计量模型中加入要素资源错配的二次项，来检验非线性关系。本文分别构建以下以技术创新投入和技术创新产出为被解释变量，要素资源错配（劳动力错配和资本错配）为核心解释变量的计量模型：

lntiiit=α0+α1lntiii，t-1+α2krmit+α3lrmit+α4krm2it+α5lrm2it+α6krmit×ownit+α7lrmit×ownit+∑βicontroli+μi+εit（28）

lntioit=α0+α1lntioi，t-1+α2krmit+α3lrmit+α4krm2it+α5lrm2it+α6krmit×ownit+α7lrmit×ownit+∑βicontroli+μi+εit（29）

其中，i和t分别为企业和年份，μ为个体效应，ε为随机误差项，其他变量含义同上。

（二）数据来源及处理

本文采用高技术产业A股上市公司数据进行研究，相关指标数据来自CSMAR数据库，并参考和对比相关公司年报。基于所获数据的特点和研究分析的需要，剔除ST、PT类企业，剔除存在大量缺失值的企业，最终获取时间跨度為2012—2016年246家上市公司数据，1 230个样本观测值。包括除宁夏、青海、海南和港澳台之外的28个省份;参考经济合作与发展组织（OECD）对高技术产业的分类标准和CSMAR数据库对高技术产业的行业划分，将高技术产业划分为医药制造业（行业1），计算机、通信和其他电子设备制造业（行业2），铁路、船舶、航空航天及其他运输设备制造业（行业3），医疗仪器设备及仪器仪表制造业（行业4）四大子行业。基于不同地区分析时，将28个省份划分为东中西三大地区，其中，东部地区包括北京、天津、河北、辽宁、山东、江苏、浙江、上海、广东和福建，中部地区包括内蒙古、黑龙江、吉林、山西、河南、安徽、湖北、湖南和江西，西部地区包括广西、陕西、甘肃、四川、贵州、重庆、云南、新疆和西藏。为减少极端值的影响，根据需要对连续性变量分别按1%和99%分位数进行了Winsorize处理。主要变量的描述性统计如表1所示。

（三）回归结果

所构建的动态面板模型可能存在内生性问题，导致回归结果出现偏误，为了克服差分GMM和水平GMM弱工具变量和偏误问题，本文采用系统GMM方法对动态面板数据模型进行估计，不但可以克服弱工具变量问题，而且能够提高估计效率，较好地解决内生性问题。所有回归结果均通过了检验，模型估计有效。

1.基于全部样本的回归结果分析

表2是全样本要素资源错配对技术创新的回归结果。

从表2可以看出，第一，技术创新存在显著的循环累积效应。技术创新投入和技术创新产出滞后一期系数均通过了显著性水平检验且均为正值，表明技术创新存在循环累积效应。这一结论与多数学者的研究成果一致[17-18]。第二，资本错配对技术创新的影响并不显著。无论是技术创新投入还是技术创新产出，劳动力错配系数均通过1%的显著性水平检验，其平方项系数未通过显著性检验，表明劳动力错配对技术创新具有明显的促进作用。这不同于李平和季永宝[19]的研究，可能因为所有制歧视和规模歧视导致的劳动力错配造成了利润损失，促使高技术产业上市公司通过技术创新进行弥补，并可能存在所有制差异，但实证结果表明资本错配和劳动力错配对技术创新的影响并未呈现显著的所有制差异。第三，在控制变量中，仅有取自然对数的资本密集度和有形资产率通过了显著性水平检验。具体地，取自然对数的资本密集度系数为正，表明资本密集度的提高促进了技术创新，较高的人均资本水平可以为技术创新提供坚实的研发条件和基础，并且在长期中相互促进[20]，对技术创新产生了更高的需求，促进了技术创新水平的提高。有形资产率系数为负，表明有形资产率挤占了技术创新，明显抑制了高技术产业上市公司技术创新。

2.基于行业差异的回归结果分析

表3是基于行业差异的要素资源错配对技术创新的回归结果。

从表4可以看出，第一，东部地区高技术产业上市公司技术创新存在循环累积效应。与全部样本的结论相同，东部地区资本错配未对技术创新产生显著影响。劳动力错配系数均通过了1%的显著性水平检验且为正值，但其平方项仅对技术创新投入系数通过了显著性水平检验且为负值，表明劳动力错配对东部地区高技术产业上市公司技术创新有正向作用，且在非线性条件下呈现倒U型趋势。劳动力错配与所有制性质的交互项对技术创新产出系数通过了1%的显著性水平且为负值，表明相比于非国有高技术产业上市公司，劳动力错配不仅会减缓对东部地区国有高技术产业上市公司技术创新产出的促进作用，并最终呈现负向影响

，表明中部地区，劳动力错配在促进高技术产业上市公司技术创新产出水平提高的同时，会减缓对国有高技术产业上市公司技术创新产出水平的促进作用。第二，中部地区高技术产业上市公司技术创新存在循环累积效应。劳动力错配对技术创新投入系数通过了5%的显著性水平检验且为正值，表明与全部样本和东部地区模型类似，劳动力错配促进了中部地区高技术产业上市公司技术创新投入水平的提高。第三，西部地区高技术产业上市公司技术创新存在循环累积效应。劳动力错配及其与所有制性质的交互项对技术创新产出系数均通过了1%的显著性水平检验且分别为正值和负值，对国有高技术产业上市公司技术创新产出的净作用为负。

4.基于所有制性质的回归结果分析

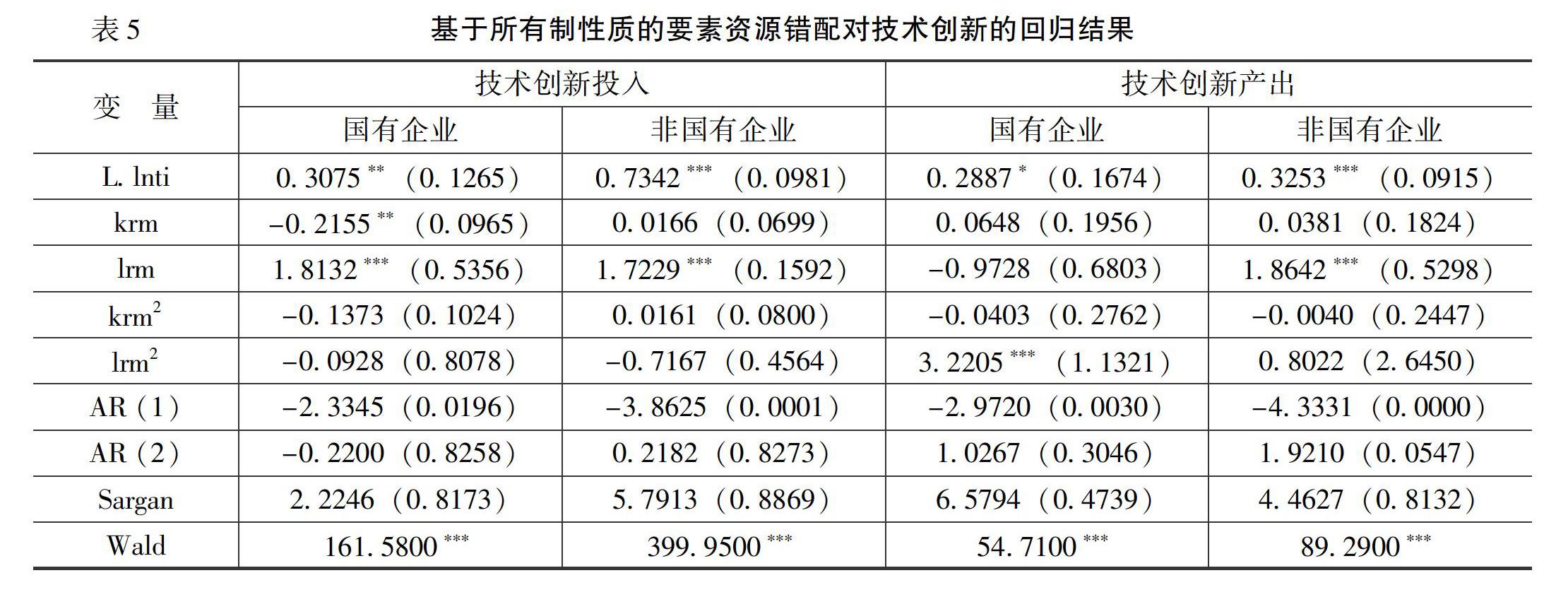
表5是基于所有制性质的要素资源错配对技术创新的回归结果。

从表5可以看出，第一，国有高技术产业上市公司技术创新存在循环累積效应。在技术创新投入中，资本错配系数和劳动力错配系数分别显著为负值和正值，表明对国有高技术产业上市公司来说，资本错配抑制了技术创新投入水平，而劳动力错配则对技术创新投入起着较大的促进作用，要素资源错配对技术创新产出则没有显著影响。这可能是由于我国金融制度的特殊安排，随着因循赶超型制度提供的模仿红利消失，资本资源的配置不当不利于国有高技术产业上市公司技术创新投入水平的提高。第二，非国有高技术产业上市公司技术创新存在循环累积效应。劳动力错配系数均通过了1%的显著性水平检验，劳动力错配促进了非国有高技术产业上市公司技术创新水平的提高。控制变量中，取自然对数的资本密集度系数和有形资产率系数均通过了较高的显著性水平检验，资本密集度会提升非国有高技术产业上市公司的技术创新水平，而有形资产率则有着负向影响。企业规模对技术创新产出的系数通过了5%的显著性水平检验且为负值，表明企业规模的扩大抑制了非国有高技术产业上市公司技术创新产出水平的提高。

（四）稳健性检验

考虑到模型估计结果的稳健性，基于全部样本分析时，本文分别进行了最小二乘估计、固定效应估计和差分GMM估计，将其估计结果与系统GMM估计结果进行对比分析，以提高结果稳健性。对系统GMM估计采用逐个引入企业特征变量的方法进行估计，测度企业特征变量对技术创新的影响并保证估计结果的稳健性。

限于篇幅，稳健性检验结果未在正文列出，留存备索。通过Hausman检验选择固定效应，差分GMM和系统GMM均通过了扰动项自相关检验和过度识别检验，在不同模型回归结果中，各变量回归系数大小、符号和显著性基本稳定，得到的研究结论与前文一致。

在进行异质性分析时，本文仍然使用最小二乘估计、普通面板估计和差分GMM估计等方法，与系统GMM估计结果进行比较，检验结果稳健。基于行业、地区和所有制性质分析时，各个模型均通过了F检验或Wald检验，差分GMM和系统GMM均通过了扰动项自相关检验和过度识别检验。在不同行业、不同地区和不同所有制性质的回归模型中，四种方法的回归结果基本保持一致，变量系数大小、符号和显著性比较稳定，研究结论并未发生实质性改变。

四、研究结论与政策启示

本文构建理论模型，利用2012—2016年我国高技术产业上市公司微观数据，建立动态面板数据模型，采用系统GMM估计方法分析要素资源错配对技术创新的影响。研究结果显示：（1）除个别模型外，技术创新存在明显的循环累积效应。（2）从全部样本来看，劳动力错配显著提高了高技术产业上市公司的技术创新水平，资本错配的影响则不显著。资本密集度提高了技术创新水平，有形资产率则对技术创新有抑制作用。（3）分行业来看，资本错配抑制了医药制造业上市公司的技术创新水平，对铁路、船舶、航空航天及其他运输设备制造业上市公司的技术创新投入则有促进作用;劳动力错配对四大行业高技术产业上市公司技术创新投入和技术创新产出均有显著正向影响;要素资源错配与技术创新呈现非线性关系。在交互项影响中，资本错配对铁路、船舶、航空航天及其他运输设备制造业上市公司技术创新投入，劳动力错配对医药制造业上市公司技术创新投入、对计算机、通信和其他电子设备制造业上市公司技术创新产出均呈现显著的所有制差异。（4）分地区来看，资本错配没有显著影响，而劳动力错配对三大地区高技术产业上市公司技术创新水平均有显著促进作用，且在东部和西部地区模型中呈现显著的所有制差异。（5）分所有制性质来看，资本错配降低了国有高技术产业上市公司的技术创新投入水平，劳动力错配对国有和非国有高技术产业上市公司技术创新投入以及非国有高技术产业上市公司技术创新产出均有显著促进作用。

本文将要素资源错配（资本错配和劳动力错配）引入高技术产业的技术创新（技术创新投入和技术创新产出）领域，构建了一个新的理论模型分析要素资源错配对技术创新的影响，并通过实证检验得出的结论具有重要的政策启示：（1）制定稳健连续的技术创新战略，保证企业技术创新投入和技术创新产出的连续性。高技术产业上市公司的技术创新存在明显的循环累积效应，因而对高技术产业上市公司来说，要制定平稳的技术创新发展战略，形成良好的企业创新投资氛围，以连续的技术创新投入带动持续的技术创新产出，维持高技术产业上市公司利润增长点，促进企业长期高效发展。（2）深化要素市场改革，建立健全要素市场的合理配置机制。针对资本错配和劳动力错配对不同行业高技术产业上市公司技術创新可能产生的促进或抑制作用，要因行业制宜，制定合理有效的行业资源分配政策，根据行业特点满足技术创新对资本资源和劳动力资源的需要;针对要素资源错配与技术创新可能呈现的非线性关系，要准确把握要素资源错配程度对技术创新影响的临界值，根据各行业和地区高技术产业上市公司的特点分配要素资源，逐步建立以创新为导向的要素资源分配制度，使要素资源错配程度保持在有利于技术创新的临界值范围内;针对要素资源错配表现出的对技术创新影响的所有制差异，要。继续深化金融市场改革，推进户籍制度改革，逐步建立资本资源和高素质人才资源流动的市场化机制，形成国有企业和非国有企业更加公平合理的资源分配环境和创新环境。（3）把握企业特征因素对企业技术创新的作用，规避要素资源错配的抑制效应。资本密集度、有形资产率和公司杠杆比率对高技术产业上市公司的技术创新活动均有显著影响，这意味着在促进要素市场化改革的同时，要充分考虑企业特征因素对技术创新的影响，根据不同行业、地区和所有制性质企业的特征，制定合理的应对措施，规避要素资源错配的负向影响，提高企业的技术创新水平。具体来说，要合理控制企业固定资产规模和企业员工人数，使企业保持较高的资本密集度;保持有形资产和无形资产比例适当，规避有形资产对技术创新资源的挤出效应;合理利用公司负债，把控公司偿债风险的同时，利用公司杠杆率撬动更多资本，满足企业技术创新对资本的需要，提高企业的技术创新水平。

参考文献：

[1] 周新苗，钱欢欢.资源错配与效率损失：基于制造业行业层面的研究[J].中国软科学，2017，（1）：183-192.

[2] Hsieh，C.T.，Klenow，P.J.Misallocation and Manufacturing TFP in China and India[J].Quarterly Journal of Economics，2009，124（4）：1403-1448.

[3] 简泽.市场扭曲、跨企业的资源配置与制造业部门的生产率[J].中国工业经济，2011，（1）：58-68.

[4] 曹玉书，楼东玮.资源错配、结构变迁与中国经济转型[J].中国工业经济，2012，（10）：5-18.

[5] Moll，B.Productivity Losses From Financial Frictions： Can Self-Financing Undo Capital Misallocation？[J].The American Economic Review，2014，104（10）：3186-3221.

[6] 姚战琪.生产率增长与要素再配置效应：中国的经验研究[J].经济研究，2009，（11）：130-143.

[7] 涂正革，肖耿.中国的工业生产力革命——用随机前沿生产模型对中国大中型工业企业全要素生产率增长的分解及分析[J].经济研究，2005，（3）：4-15.

[8] Hermes，N.，Lensink，R. Foreign Direct Investment，Financial Development and Economic Growth[J].Journal of Development Studies，2003，40（1）：142-163.

[9] Gorodnichenko，Y.，Schnitzer，M.Financial Constraints and Innovation：Why Poor Countries Dont Catch up[J].Journal of the European Economic Association， 2013， 11（5）：1115-1152.

[10] Li，H.C.，Lee，W.C.，Ko，B.T.What Determines Misallocation in Innovation？ A Study of Regional Innovation in China[J].Journal of Macroeconomics，2017，52（6）：221-237.

[11] 张杰，周晓艳，李勇.要素市场扭曲抑制了中国企业R&D？[J].经济研究，2011，（8）：78-91.

[12] 戴魁早，刘友金.要素市场扭曲与创新效率——对中国高技术产业发展的经验分析[J].经济研究，2016，（7）：72-86.

[13] 李龙筠，谢艺.中国创业板上市公司创新能力评估[J].经济学家，2011，（2）：93-102.

[14] 邵挺.金融错配、所有制结构与资本回报率：来自1999～2007年我国工业企业的研究[J].金融研究， 2010，（9）：47-63.

[15] Melitz，M.J.The Impact of Trade on Intra-Industry Reallocations and Aggregate Industry Productivity[J].Econometrica，2003，71（6）：1695-1725.

[16] 吴延兵.不同所有制企业技术创新能力考察[J].产业经济研究，2014，（2）：53-64.

[17] 吕承超.中国高技术产业专业化比多样化更有利于区域产业创新吗？[J].研究与发展管理，2016，（6）：27-37.

[18] 张伟峰，慕继丰，万威武.基于企业创新网络的技术路径创造[J].科学学研究，2003，（6）：657-661.

[19] Acemoglu，D.，Aghion，P.，Zilibotti，F.Distance to Frontier， Selection， and Economic Growth[J].Journal of the European Economic Association，2006，4（1）：37-74.

[20] Howitt，P.，Aghion，P.Capital Accumulation and Innovation as Complementary Factors in Long-Run Growth[J].Journal of Economic Growth，1998，3（2）：111-130.

[21] 白俊红，卞元超.要素市场扭曲与中国创新生产的效率损失[J].中国工业经济，2016，（11）：39-55.

[22] 康志勇.金融错配阻碍了中国本土企业创新吗？[J].研究与发展管理， 2014，（5）：63-72.