基于分阶段迭代模型的产品设计任务分布方案优化

田启华 鄢君哲 董群梅 张玉蓉 周祥曼

(1. 三峡大学 机械与动力学院， 湖北 宜昌 443002； 2. 国电大渡河检修安装有限公司， 四川 乐山 614000)

完全的并行迭代模型假设所有的耦合集任务同时并行执行，而在实际的产品开发过程中，部分任务由于设计要求的改变或资源约束等原因总存在执行顺序先后问题，优先完成的任务必须要等待后完成的任务，故完全并行迭代模型已经不再适用，故需要采用分阶段迭代模型处理．针对分阶段迭代模型中任务分布方案优化的问题，国内外学者进行了相关的研究，并取得了相应的成果．如：Smith等[1]将工作转移矩阵(work transformation matrix, WTM)运用到二阶段迭代模型中，得到了有利于减少项目开发时间成本的任务分配方案；陈卫明等[2]通过启发式算法对二阶段迭代模型执行时间进行求解，但是没有给出寻求最优的二阶段迭代模型任务分布方案的可行方法；肖人彬等[3]针对分阶段迭代模型中的资源分配问题，运用遗传算法得到了较优的资源分配方案；田启华等[4]运用动态规划法对二阶段迭代模型的任务分布方案进行寻优，并证明了该方法能在一定程度上弥补启发式方法容易陷入局部最优解的不足．上述文献从不同角度研究了分阶段迭代模型中任务分布方案优化的问题．但是，不同算法对具体迭代模型的适用性较为有限，甚至需要对算法进行一定的改进才能成功获取一个较优解．

鉴于以上研究的不足，引入Markov Chain理论．假设在设计任务的迭代过程中，每次只有一个任务执行，因此其过程转化为串行设计迭代过程，而耦合设计任务集总的执行时间等于那些任务所花时间的总和．针对此假设，耦合设计任务集可以描述成Markov Chain模型并用Markov Chain分析方法进行分析．由于Markov Chain分析方法是建立在随机统计分析基础之上，因此算法简单，求解过程清晰明了，无需借助计算机编程就能得到结果．当耦合任务规模较小时，采用马尔可夫链(Markov Chain)方法对串行迭代过程进行建模分析，可以通过计算纯粹顺序情况下的总迭代时间，来确定最优的耦合集任务执行顺序．

目前Markov Chain在迭代建模中也已经得到许多成功应用．例如：石坤等[5]运用Markov Chain理论，将量化的流程图转化为Markov概率转移图，根据概率转移图列出概率转移矩阵，求解矩阵的平稳分布，利用平稳分布来解出驾驶人行为的可靠性；南爱强等[6]结合经典灰色理论，构建了一种新型的灰色Markov Chain模型，相较传统的经典灰色理论具备较高的预测精度．设计结构矩阵能简化并有效地描述、分析信息流和迭代循环等信息交互关系，具有较强的问题描述能力[7-8]，还能很好地适应矩阵运算，被广泛地应用于产品开发领域的研究中．目前，DSM在耦合集迭代的求解问题上已经得到不少应用，例如杨沁等[9]分析了需求节点之间的矛盾，提出了一种基于DSM的客户需求表达方法；钱艳俊等[10]充分利用矩阵运算的特点，提出了基于DSM的耦合活动排程．

本文在分阶段迭代模型的基础上，以缩短产品开发过程的时间成本为目标，引入设计结构矩阵，运用Markov Chain方法对设计任务的迭代过程进行分析，得到不同任务分布方案下执行时间、任务周期和返工概率的关系，提出一种基于分阶段迭代模型的产品设计任务分布方案优化．

1 分阶段迭代模型的求解

分阶段迭代模型是在完全并行迭代模型的基础上发展而来的，是将部分任务延迟执行的情况加以考虑，其求解方法是将整个耦合任务集分成若干个子集，并将这些任务子集分配到不同的阶段中去执行．在迭代过程中，整个耦合任务集通常包含有多个设计任务(假设任务个数为m)，可能的迭代方式包括一阶迭代、二阶迭代、……、m阶迭代．为了便于研究说明，本文以m阶迭代为研究对象，即假定每个阶段均只有一个任务被执行的情况．

为了描述分阶段迭代模型中各任务的分布情况，定义对角线矩阵K为任务分布矩阵，表示为：

(1)

式中，矩阵K对角线上元素k11、k22、…，kij，…、kmm取值为0或者1(其中i=j，i=1，2，…，m)，当取值为0时，表示第i个任务不在当前指定的阶段被执行，当取值为1时，表示第i个任务在当前指定的阶段被执行．

根据文献[11]，分阶段迭代模型第1阶段的执行时间T1为：

T1=Z(I-K1RK1)-1K1u0

(2)

式中，Z是任务周期矩阵；R是返工概率矩阵；初始的工作向量u0是全1向量，表示在第一次迭代中所有任务都需要同时执行；I为单位矩阵，矩阵K1是一个对角矩阵，描述了任务在第1阶段迭代过程中的执行情况，矩阵K1对角线上第i行第j列元素的取值定义如下：

第2阶段需要的执行时间T2为：

T2=Z(I-K2RK2)-1(K2-K1)u0

(3)

式中，矩阵K2为第2阶段的任务分布矩阵，描述了任务在第2阶段迭代过程中的执行情况，矩阵K2对角线上第i行第j列元素的取值定义如下：

第S阶段所需时间Ts为：

Ts=Z(I-KsRKs)-1(Ks-Ks-1)u0

(4)

式中，矩阵Ks为第s阶段的任务分布矩阵，描述了任务在第s阶段迭代过程中的执行情况，矩阵Ks对角线上第i行第j列元素的取值定义如下：

将所有阶段的执行时间求和，并对其取模，可得到迭代过程的总时间成本值为T：

(5)

对于一个包含有多个任务的分阶迭代过程，通过设计一个较优的任务分布可以减少迭代过程的时间成本．因此，从迭代过程本身出发，通过研究DSM中任务周期矩阵Z、返工概率矩阵R与时间成本之间的关系，以得到有利于时间成本下降的任务布局方法．

2 任务分布方案的优化策略

DSM是一个具有相同行列标志的矩阵，能够以直观、形象、最优的分析形式显示迭代过程中任务之间的耦合关系．本文采用DSM对耦合集中任务的执行状态进行描述．例如，对于一个包含有A、B、C、D4个任务的耦合集的四阶迭代过程，若A、B、C、D任务分别在第1阶段、第2阶段、第3阶段、第4阶段被执行，结合文献[12-13]中DSM的设计方法，该迭代过程对应的设计结构矩阵如图1所示．

图1 设计结构矩阵

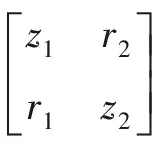
由图1可知， DSM主要包括对角线和非对角线单元．其中，z1、z2、z3、z4为DSM对角线上的元素，描述了耦合集中各任务的执行周期值；是DSM非对角线的元素，表示在迭代过程中任务的返工概率．图1设计结构矩阵对应的任务周期矩阵Z和返工概率矩阵R分别为：

根据公式(1)～(5)可知，迭代过程的执行时间不仅与任务的分布矩阵Ks有关，还与任务周期矩阵Z、返工概率矩阵R直接相关，而任务周期矩阵Z、返工概率矩阵R分别由DSM中对角线上的元素、非对角线上的元素组成，且各阶段迭代的任务分布矩阵Ks也是由DSM中任务的执行顺序决定．

为了减小问题分析难度，取DSM中任务A、B进行分析，并简化DSM中元素的记法，即：z1、z2分别是任务A和B的执行周期值，取值为整数，表示任务A和B分别独立执行所需的时间；r1、r2分别是任务A、B的返工概率，其取值范围均为0到1，r1表示每次任务A完成后，引起任务B要重做的概率，而r2表示每次任务B完成后，引起任务A要重做的概率，对应的DSM如下：

A B

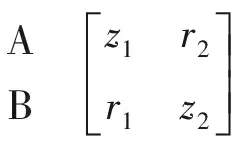
(6)

对该迭代过程建立Markov Chain模型，如图2所示．任务分布优化相当于确定哪条虚箭线包括在链的模型中．

图2 2×2阶迭代的Markov Chain模型

图2中虚线指向A，表示任务A在第1阶段先执行，任务B在第2阶段被执行，记为A-B方案；若虚线指向任务B，则为B-A方案．

定义TA和TB分别表示在同一迭代过程中任务A和任务B的执行时间，根据图2的迭代过程，参考文献[14]中运用Markov Chain对串行迭代过程进行建模的方法，可得到如下矩阵线性方程组：

(7)

用TA-B和TB-A分别表示A-B、B-A方案的时间成本，分别求解两种任务分布的TA-B和TB-A关于周期值z1、z2和返工概率值r1、r2的数学关系式．

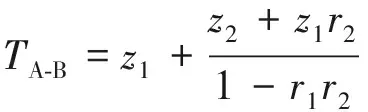
(8)

(9)

通过上述分析，可知对于包含任务A和B的耦合集迭代过程，其可能的任务分布方案及对应的DSM和时间成本见表1．

表1 两种方案下的DSM及时间成本T

为了便于分析任务分布方案的优化策略，先假设A-B方案的时间成本小于B-A方案，即

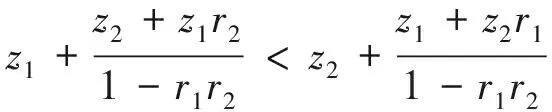
(10)

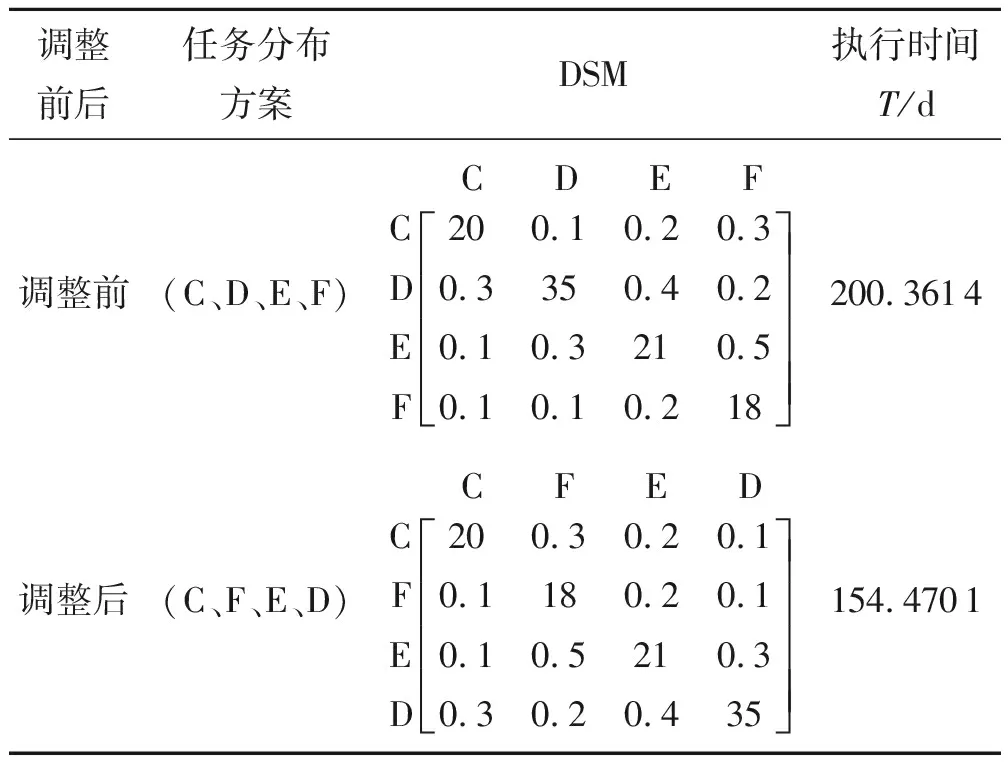
由于00，将公式(10)中不等式的两边同乘以(1-r1r2)，整理后，可以得到z1r2(1-r1)

(11)

结合式(6)对应的DSM可知r1、r2对应为DSM中的非对角线元素，z1、z2对应为DSM中的对角线元素．分析式(11)可知，当任务A的执行周期z1小于任务B的执行周期z2、任务B的返工概率r2小于任务A的返工概率r1时，式(10)、式(11)恒成立，即TA-B

《浙江省海洋功能区划（2011-2020 年）》（2018 年修订版）正式发布（省厅办公室） .........................11-13

为了获得时间成本较低的任务分布，结合上述分析过程，执行周期长的任务应优先安排在DSM对角线的右下方，返工概率大的值应放置在DSM对角线的下方，这种任务布局是有利于时间成本减少的．

以上分析过程，是以迭代过程中的两个任务为对象来分析的，将任务分布方案的优化问题，转化成具体的计算推理，进而抽象性地得出了有利于时间成本的布局方法．虽然理论过程存在一定的局限性，但是，该研究方法是从迭代过程的本身出发进行的计算推导，与目前已有的引入优化算法来获取较优的任务布局相比，是解决分阶段迭代过程方案优化的另一种途径．下面通过示例计算说明本文提出方法的有效性．

3 实例分析

以某型号照相机开发过程为例进行说明．该产品开发过程包括功能定义(任务A)、概念设计(任务B)、快门装置设计(任务C)、取景装置设计(任务D)、相机体设计(任务E)、卷片装置设计(任务F)、光学镜头设计(任务G)、光圈设计(任务H)等8个任务，其中任务C、任务D、任务E以及任务F等4个任务构成带循环信息流的耦合集[1，12]．假定照相机开发过程中C、D、E、F分别在第1、2、3、4阶段被执行，对应的任务分布形式表示为(C、D、E、F)，DSM对角线上的元素表示任务C、D、E、F各自独立执行的周期，非对角线上元素表示各任务的返工概率，该方案下的DSM如下．

C D E F

(12)

由周期矩阵Z、返工概率矩阵R的定义，可得到照相机开发的Z、R矩阵分别为：

在迭代初始阶段，初始工作向量u0为全1列向量，即：u0=[1 1 1 1]T，任务C、D、E、F分别被分配到1、2、3、4阶段去执行执行，根据第2节关于任务分布矩阵K的元素的定义，可得各阶段的任务分布矩阵分别为：

(13)

将Z、R、K1、K2、K3、K4、u0、I分别带入公式(13)，可以得到基于任务分布方案(C、D、E、F)的时间成本为200.361 4个时间单位．

下面应用本文提出任务分布优化方法对DSM进行重新调整．为减少照相机开发的时间成本，在对DSM进行调整的过程中，尽可能让周期较长的任务稍后执行，高返工概率值置于DSM对角线的下方，分析公式(12)中DSM的数据结构，需要将返工概率较高的0.5和0.4调整到对角线的下方，周期最长的任务D尽可能安排在靠后阶段被执行，可将DSM第4行和第2行进行交换，再将第2列与第4列交换，调整过程如图3所示．

图3 DSM的结构调整过程

图3得到的调整后的DSM的任务分布形式为表示任务C第1阶段被执行，任务F在第2阶段被执行，任务E在第3阶段被执行，任务D在第4阶段被执行，即调整后的DSM为：

C F E D

(14)

调整后的DSM的任务矩阵分别为：

照相机开发过程基于调整后的DSM的Z、R矩阵分别为：

将Z、R、K1、K2、K3、K4、u0、I分别代入公式(13)，可得到任务分布方案(C F E D)的时间成本值为154.470 1．对DSM进行调整前，周期最长的任务D在第2阶段被执行，返工概率较高的数值0.5和0.4在对角线的上方；调整后的DSM中，周期最长的任务D在最后段被执行，返工概率较高的数值0.5和0.4均在对角线下方，时间成本为154.470 1个时间单位，见表2．

表2 基于DSM优化策略前后的任务布局及时间成本

由表2可知，调整前照相机开发过程的时间成本为200.361 4个时间单位，调整后的时间成本为154.470 1个时间单位，调整后减少了45.891 3个时间单位，时间成本下降了22.904 2%．以上分析结果表明，对于分阶段迭代模型任务分布优化问题，采用本文提出的基于DSM优化方法，即周期长的任务稍后执行，返工概率高的值放在DSM对角线的下方，是有利于时间成本下降的任务布局．

4 结 语

本文研究的基于分阶段迭代模型的产品设计任务分布方案优化方法，通过运用Markov Chain方法来分析任务周期和返工概率对不同任务分布时间成本的影响，并通过构建任务分配衍生矩阵，简化了分阶段耦合集设计任务分配的数学模型．运用该方法对分阶段迭代模型的任务分布进行优化，以某型号照相机开发过程为例，验证了该分析方法是可行且有效的，并能获取一个能有效减少产品开发过程的时间成本的相对较优解，对实际产品开发有一定的参考意义．