植保机喷杆的鲁棒保性能控制*
王向东,魏 浩
(沈阳工业大学 信息科学与工程学院,沈阳 110870)
在众多植物保护方法中,化学防治凭借其高效和防治及时等特点,依旧是对作物进行病虫草害防治的主要方法.植保机械对化学防治的有效实施起着非常重要的作用,但目前我国植保机械仍然存在结构简单、技术较为落后等问题,从而导致农药残留超标和环境污染等众多问题[1-2].因此,对如何提高植保机械施药效率、自动化水平等相关课题的研究显得至关重要.
喷杆式喷雾机作为一种重要的植保机械,具有喷雾压力高、雾化效果好和作业效率高等优点,随着我国农业种植规模的快速扩大,其应用也越来越广[3].但在日常的农业喷药时,由于喷杆式喷雾机大多具有较长的喷杆,所以田地的不平整性很容易使喷杆产生不利于喷药均匀性的有害振动.为此,不少学者针对如何降低这类有害振动展开了大量研究并得出许多有效的控制方法,如零极点配置[4-5]和主动力控制[6-7]等.上述这些控制方法虽然都取得了很好的控制效果,但均对模型中存在的不确定因素考虑得不够充分,而在实际工程问题中,不确定因素或不可预见因素的存在是难以避免的,这些因素在模型中表现为不确定性,某些不确定性的存在对系统的运行品质会产生不良影响[8].
本文将文献[5]的缆绳悬架传递函数模型转化为状态空间模型,并考虑到模型中存在的不确定性和外部扰动,应用鲁棒保性能控制理论进行控制器的设计,并引入H∞控制理论抑制模型中的外部扰动.鲁棒保性能控制不仅可以使存在不确定性的喷杆闭环系统具有二次稳定性,而且还能使该系统满足某一确定的性能指标上界.最后,为了更直观地判断出喷杆能否快速平稳下来,选取喷杆的转角和角速度作为评判控制器性能的指标,并通过仿真验证控制器的性能.
1 模型与问题描述
1.1 模型描述
图1为文献[4-5]采用的缆绳悬架结构示意图,Deprez和Anthonis等人首先针对缆绳悬架结构进行了拉格朗日方程建模,得出了该结构传递函数的基本结构,之后通过频率响应函数法求出了该传递函数中相应的各个参数,最终得到的传递函数为
文献[5]给出了图1结构中电机的传递函数,即

图1 缆绳悬架结构示意图Fig.1 Schematic diagram of cable suspension structure
由于在建模过程中实验数据不一定完全精确,从而使该传递函数的各项系数难免存在误差.文献[4-5]中的喷杆与电机的传递函数相乘后所得模型只描述了系统外部控制信号与喷杆转角之间的关系,存在一定的局限性,导致能够应用在该模型上的控制方法相对较少.而状态空间模型可以很好地反映出系统内部状态及状态之间的关系,正好弥补了上述局限.本文将上述缆绳悬架的传递函数与电机的传递函数相乘并转化为状态方程,得到了状态空间模型,其表达式为
(1)

考虑到系统模型存在不确定性,将式(1)转换为
(2)
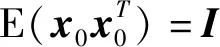
1.2 问题描述
为了尽可能加快系统状态变量的响应速度,减小误差,并且兼顾系统的输入能量,给出二次型性能指标,其表达式为

(3)
式中,Q和R为给定的对称正定矩阵.
针对系统(2)设计状态反馈控制器,可得
u(t)=Kx(t)
(4)

2 鲁棒保性能控制器设计
定义1当w(t)=0时,如果存在一对称正定矩阵P,对于所有的不确定性,使得二次型Lyapunov函数V(x,t)对时间t的导数满足

成立,则系统(2)为二次稳定的.
引理1[9]对于任意具有适当维数的矩阵D、F(t)、E,且F(t)满足FT(t)F(t)≤I,则对任意的ε>0,DF(t)E+ETFT(t)DT≤εDDT+ε-1ETE.
本文给出在控制器(4)作用下,存在不确定性的系统(2)二次稳定,且满足性能指标式(3)的条件.
定理1对于给定的系统(2),如果存在正定对称矩阵P、矩阵K和标量ε>0,使得

(5)
成立,则当w(t)=0时,系统(2)在控制器(4)的作用下是二次稳定的.
证明:将控制器(4)代入系统(2)中可得
选取Lyapunov函数,即
V(x,t)=xTPx
则
xT[(A+BK)TP+P(A+BK)+
(MF(t)Na+MF(t)NbK)TP+
P(MF(t)Na+MF(t)NbK)]x
令
L=(A+BK)TP+P(A+BK)+
(MF(t)Na+MF(t)NbK)TP+
P(MF(t)Na+MF(t)NbK)
根据引理1可知
L≤(A+BK)TP+P(A+BK)+εPMMTP+
ε-1(Na+NbK)T(Na+NbK)
令
S=(A+BK)TP+P(A+BK)+εPMMTP+
ε-1(Na+NbK)T(Na+NbK)+Q+
KTRK
则
(6)
当S<0时,即矩阵不等式(5)成立时,系统满足定义1,则闭环系统是二次稳定的,定理1得证.
定理2对于给定的系统(2),如果存在正定对称矩阵P、矩阵K、标量ε>0和标量γ>0,使得

(7)
成立,则系统(2)在控制器(4)作用下满足H∞性能约束.
考虑性能指标,即
则
V(x,t))dt

xT(t)x(t)-γ2wT(t)w(t)+xTSx=
令

定理3对于给定的系统(2),如果存在正定对称矩阵Z、矩阵D、标量ε>0和标量γ>0,使得

(8)
成立,则系统(2)在控制器(4)作用下满足性能指标(3).
证明:根据定理1可知,系统(2)在控制器(4)作用下满足式(6),即
(9)
将式(9)两边对时间t从0~∞积分,并根据系统的二次稳定性可得

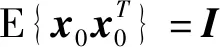
即性能指标的上界转化为正定对称矩阵P的迹.
将矩阵不等式(7)分别左乘和右乘矩阵diag(P-1,I,I,I,I,I),并记Z=P-1,D=KP-1,可得线性矩阵不等式(8),定理3得证.使用Matlab中的LMI工具箱进行求解,控制器由式(4)转化为
(10)
3 系统仿真
为了验证控制器(10)对喷杆系统(2)的有效性,取不确定项ΔA与ΔB中的未知参数为
取给定的对称正定矩阵Q与R为

取标量参数ε=0.000 2,γ=0.5.应用Matlab中的LMI工具箱解线性矩阵不等式(8),可得

D=[-0.180 1,0.005 4,-0.000 2,-0.000 4]
根据Z=P-1可知

根据矩阵P的特征值大于零可知,矩阵P为正定对称矩阵.根据D=KP-1可知,控制器的参数矩阵为
K=[-0.970 4,-1.607 6,-0.993 9,-1.045]

由图2~7可以看出,在角度相同、角速度不同的三种情况下,对比曲线即使未考虑系统存在的不确定性,其响应速度仍然较慢且超调量较大,而且喷杆角度或多或少存在一定的稳态误差,喷杆最终无法回到与地面相平行的位置.而鲁棒保性能控制器作用下的响应曲线,虽然考虑了系统存在的不确定性和外部扰动,但无论是角度还是角速度,其响应速度和超调量均明显优于对比曲线,这表明鲁棒保性能控制器对喷杆有害振动的抑制效果非常明显,且在三种情况下喷杆角度的稳态误差均小于0.05 rad,基本平行于地面,远远小于对比曲线的稳态误差.

图2 情况1)下角度随时间变化曲线Fig.2 Angle changing with time in case of No.1

图3 情况1)下角速度随时间变化曲线Fig.3 Angle velocity changing with time in case of No.1

图4 情况2)下角度随时间变化曲线Fig.4 Angle changing with time in case of No.2

图5 情况2)下角速度随时间变化曲线Fig.5 Angle velocity changing with time in case of No.2

图6 情况3)下角度随时间变化曲线Fig.6 Angle changing with time in case of No.3

图7 情况3)下角速度随时间变化曲线Fig.7 Angle velocity changing with time in case of No.3
4 结 论
本文将鲁棒保性能控制理论与H∞控制理论引入到植保机喷杆的平衡控制中,并且在模型中考虑了不确定性和外部扰动,得出了既能快速抑制喷杆有害振动,又能使系统满足给定性能约束和性能指标的鲁棒保性能控制器.分别在三种不同的情况下对该控制器的有效性进行了验证,仿真结果表明,当植保机喷杆处于振动状态时,本文设计的控制器可使喷杆快速回到平行于地面的状态,有效抑制喷杆的有害振动.

