基于线性规划算法的源-网-荷互动最优潮流模型*

宋玮琼，羡慧竹，丁 宁，陈迎霞，景治军

(1.国网北京市电力公司 电力科学研究院，北京 100162；2.北京前景无忧电子科技有限公司 总部，北京 100070)

为充分利用风能和太阳能，我国正在大力发展风电与光伏发电，希望实现能源的集中开发及远程输送.但在具体的应用过程中，由于通道的输送能力存在较大的限制，风电和光伏发电均存在严重的弃风、弃光现象.此外，在日趋成熟的能源市场中，电网的部分业务将逐渐向市场资本开放，电力资源的价格也将随市场的供求关系而浮动，导致电网负荷产生较大的变化.而引入可以优化利用的“源-网-荷”模型，可以协调解决电网中负荷消纳和传输困难等问题.

新能源本身存在波动性和随机性，所以在新能源转化为电能后，电网的发电端无法保证电能输送的稳定性，同时，电源、电网和负荷之间也存在着相互影响和制约，进而增加了电网调度的困难.如何改善电网调度和运行效率，实现“源-网-荷”之间的优化互动，成为了研究热点.文献[1]提出了可中断负荷的方式来促进电网调峰；文献[2]提出了使用可中断负荷作为最优潮流的调节方法；文献[3]认为在电网中使用互动载荷有利于形成最优潮流的优化模型；文献[4]详细分析了电网中发电端和用电端的广域“源-荷”互动优化模式；文献[5]研究了新能源利用中，柔性负荷的供需调度模型.尽管众多学者进行了诸多研究[6-10]，但大多集中于电网系统的某些技术领域[11-15]，缺少系统性的优化研究.本文针对风能、光能等新能源利用中的弃风、弃光问题，结合电价松动的改革现状，基于传统的最优潮流模型，提出了基于线性规划算法的“源-网-荷”互动最优潮流模型，不但系统优化了电网调度策略，而且减少了模型中的冗余变量，简化了计算方法.

1 柔性负荷

柔性负荷通常可以分为可中断和激励两种负荷，其主要作用是保障新能源电力的稳定性，即削峰填谷，同时还提供一些辅助服务.在电力系统的运行过程中，柔性负荷在保证电网正常运行的前提下，通常使用调节、中断等方法来满足电力系统总功率的供需平衡，即柔性负荷具有可调节和可中断的性质.电力系统一般需要建立相关的数学模型来研究关于柔性负荷的可调节、可中断等性质.

2 互动最优潮流模型

为了构造“源-网-荷”互动的最优潮流模型，基于传统的最优潮流模型，本文引入了具有可调节、可中断等调节性质的柔性负荷作为保障系统功率供需平衡的调节变量；其次，在一定时间内，本文在电力系统的用电端调节了单位用电量的净边际收益(净边际收益=边际收益-边际成本).通过上述调整措施的优化，电力系统最终可以实现净边际收益的最大化.系统的净边际收益，即整个模型的目标函数可以表示为

(1)

式中，NL为电力系统中所有负荷节点的集合；NB为系统中所有电力输送线路的集合；NG为系统中所有发电节点的集合；ΔPli为系统中第i个节点调节负荷的增量；Eli为负荷节点中单位用电量的净边际收益；ΔPnb为第b条支路的功率损耗增量；Cnb为第b条支路单位功率损耗的边际成本；ΔPgi为系统第i个发电节点的功率增量；Cgi为系统发电节点单位发电量的边际成本.

在目标函数确定之后，还需要在模型中设定相应的约束条件.一般根据约束条件的类型，条件可以分为使用等式类和不等式类两种约束条件.本模型中，等式类的约束条件主要是指系统的功率平衡约束，即系统功率供需平衡、发电和负荷端节点功率平衡、系统的输电支路功率平衡；不等式类的约束条件主要包括系统输电支路的数量和容量约束、所有发电端的发电调整量的约束以及所有负荷用电调整量的约束.

在本模型中，使用了直流潮流方程构建“源-网-荷”互动最优潮流模型的线性规划模型，删除了电压和无功功率两个约束条件.其主要原因是：1)“源-网-荷”互动最优潮流模型包含了众多参数，若考虑所有的参数影响，则计算机的执行速度将急剧降低，本文的线性规划模型不考虑电压和无功功率的约束；2)由于新能源发电具有间歇性的特点，所以直流潮流方程可以达到系统的精度要求.

2.1 直流潮流方程推导

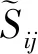
Ui[(Gi0+jBi0)U+(Gij+jBij)(Ui-Uj)]

(2)

式(2)展开可得

(3)

由于支路的电导参数远小于其导纳参数，即|Gij|≪|Bij|，而对地支路的电纳与相角差均较小，接近为零，则cosθ≈1，sinθ≈0.同时，发电节点的电压值接近单位电压，则系统的输电支路的直流潮流方程为

(4)

令Pb表示输电支路的有功功率，Bb表示输电支路导纳的对角方阵，R表示系统输电支路的关联矩阵，则直流潮流方程的矩阵表达式为

Pb=BbRθ

(5)

同理，在电力系统的第i个节点处，令Bij表示第i个节点的互导纳，其功率表达式为

(6)

其矩阵运算表达式为

P=Bθ

(7)

2.2 节点与支路功率关系矩阵推导

设节点数量是n，支路数量是b，对所有的节点和支路均进行编号，可得3个矩阵，即b×n的节点和支路的关联矩阵R，b×b的支路导纳矩阵Bb和(n-1)×(n-1)的节点导纳矩阵B′.为了得到节点功率与支路功率的具体关系，首先要确定支路和节点的编号，按照上文的叙述，分别推导出R、Bb和B′的表达式，再利用式(7)推导出P′、θ′和θ的表达式，最终得到Pb值，其具体推导流程如图1所示.

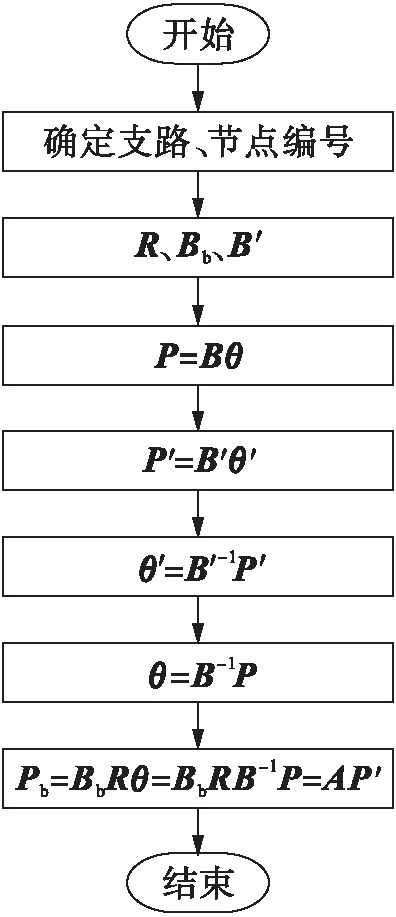
图1 节点与支路功率关系推导流程图Fig.1 Derivation flow chart for power relations among nodes and branches

2.3 互动OPF模型

由于本文模型不包括城市配电网的主网结构，所以该模型需符合以下假设条件：

1)由于大容量的变压器阻抗较小，所以输电线路可以忽略阻抗的影响；

2)由于大量使用了高压架空线路，所以可以忽略线路的电纳；

3)由于输电线路较长，而城市配电网的供电线路较短，所以线路的相角差值较小，可以认为输电线路与配电线路的相角差为0.

建立“源-网-荷”互动OPF模型，当具备了上述假设条件和推导关系后，就可以对实际模型进行简化，然后使用线性规划方法求解该模型.模型的目标函数为

(8)

在本文模型中，约束条件主要由功率、支路、发电机组、负荷等方面组成.约束条件中的等式条件包括全网功率、节点功率和支路功率等，其表达式分别为

(9)

P′g+ΔP′g-P′l-ΔP′l=B′θ′

(10)

Pb=BbRθ

(11)

其次，约束条件中的不等式条件主要由支路传输容量、发电总量和负荷调整约束组成，其表达式分别为

(12)

(13)

(14)

2.4 模型简化

(15)

同理，节点和支路功率平衡的关系矩阵为

A(P′g+ΔP′g-P′l-ΔP′l)

(16)

支路功率平衡的约束条件可简化为

(17)

将上述两式联立可得

(18)

此外，各负荷调整量和发电总量的约束可以简化为一个界约束条件，即

(19)

所以，经过简化的“源-网-荷”互动最优潮流模型的数学表达式为

3 模型求解与验证

经过线性化处理后，使用VisualStudio的Styrp求解简化模型.本文以节点数量为5的小型支路作为算例，则该节点分布模型如图2所示.令PGi表示第i个节点的潮流分布，Pbj表示第j个支路的功率上限.

图2 5节点分布模型图Fig.2 Distribution model for 5 nodes

3.1 计算数据

在模型验证的过程中，需要一些规模较小的数据，包括节点、输电线路各项参数如表1、2所示.

另外，第1、2和3个负荷节点的边际效益Eli分别可以近似为1、1.1和0.9，第4个节点是新能源发电节点，其边际成本可近似为0.01，第5个节点是常规发电节点，其边际成本可近似为0.04.根据系统的数据和拓扑，分别推导了支路的关联矩阵R、Bb和B′.

表1 节点参数Tab.1 Node parameters

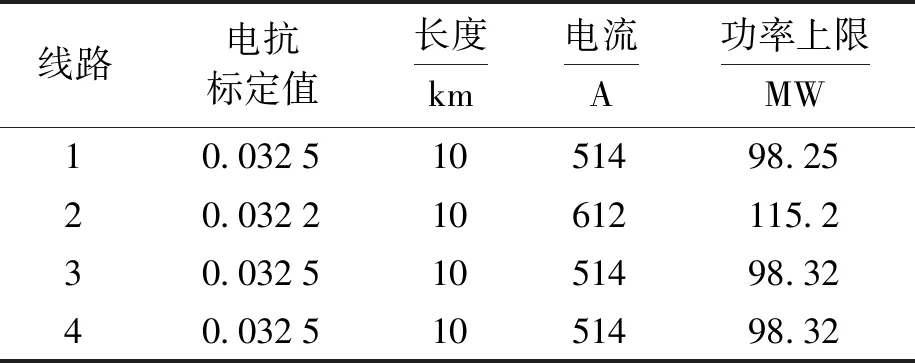
表2 输电线路参数Tab.2 Transmission line parameters

3.2 计算结果

使用节点数量为5的支路数据，就可以使用Styrp软件求解模型，求解结果如表3所示.

表3 优化后的结果Tab.3 Optimized results MW

在得出计算结果后，便可以对负荷节点制定相应的调整策略，例如：将比较重要的第1、2个负荷节点调整到最大值；第4个节点是新能源发电端，则需要减小一些发电量；第5个节点是常规发电端，则应调整为额定发电.优化之后的全系统增加边际效益的结果(单位：万元)为

ΔPli+1.1ΔPl2+0.9ΔPl3-0.01ΔPg4-0.04ΔPg5=

10+1.1×40+0.9×20-0.01×50-0.04×20=

70.7

而在优化之前，负荷节点1、2和3的净边际效益Eli分别是1、1.1和0.9，节点4的边际成本为0.005，节点5的边际成本为0.05，其计算结果如表4所示.该系统的社会净边际效益增加值(单位：万元)为

ΔPli+1.1ΔPl2+0.9ΔPl3-0.005ΔPg4-0.05ΔPg5=

10+1.1×40+0.9×20-0.005×50-0.05×20=

70.75

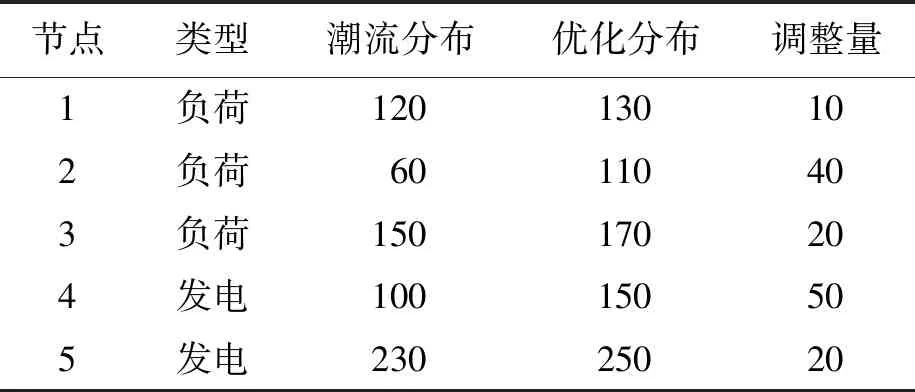
表4 优化前的结果Tab.4 Results before optimization MW

对比优化前后系统的计算结果可知：在出力方面，新能源机组和支路均受到了较大的限制.这也说明，参与“源-网-荷”互动最优潮流模型的负荷可以缓解新能源发电的能力局限问题，可以从根本上解决大规模新能源发电的弃风弃光问题.

4 结 论

针对风、光电新能源存在的弃风弃光问题，基于传统的最优潮流模型，建立了系统化的的“源-网-荷”互动最优潮流模型.通过分析计算，该模型被简化为可直接求解的线性规划问题.对小规模算例的计算结果验证了该模型的可行性.然而，通过对该模型的进一步研究发现，本模型并不适用于一些特殊的电网结构中，这一问题是下一步的研究方向.